
Proprietà del trapezio destro, relazioni e formule, esempi
UN rettangolo trapezoidale è una figura piatta con quattro lati, tali che due di essi sono paralleli tra loro, chiamati basi e anche uno degli altri lati è perpendicolare alle basi.
Per questo motivo, due degli angoli interni sono retti, cioè misurano 90º. Da qui il nome "rettangolo" dato alla figura. L'immagine seguente di un trapezio destro chiarisce queste caratteristiche:
Indice articolo
- 1 Elementi del trapezio
- 2 Relazioni e formule
- 2.1 Altezza h del trapezio
- 2.2 Perimetro P
- 2.3 Base media
- 2.4 Area
- 2.5 Diagonali, lati e angoli
- 3 Esempi di trapezi destri
- 3.1 Il trapezio come elemento di design
- 3.2 Generatore di onde trapezoidali
- 3.3 Nel calcolo numerico
- 3.4 Trave con carico trapezoidale
- 3.5 Come strumento educativo e di apprendimento
- 4 Esercizi risolti
- 4.1 - Esercizio 1
- 4.2 - Esercizio 2
- 5 Riferimenti
Elementi del trapezio
Gli elementi del trapezio sono:
-Basi
-Vertici
-Altezza
-Angoli interni
-Base centrale
-Diagonali
Descriveremo in dettaglio questi elementi con l'aiuto delle figure 1 e 2:
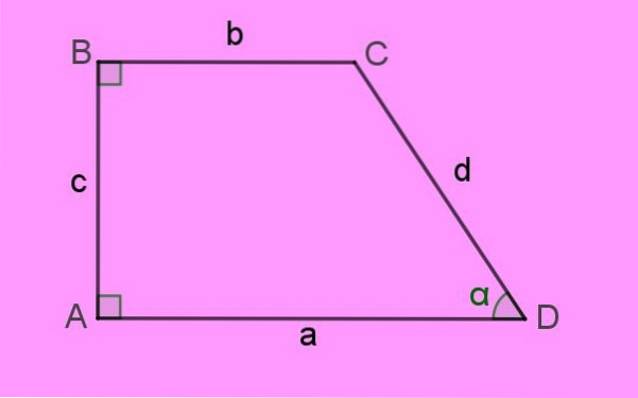
I lati del trapezio destro sono indicati con lettere minuscole a, b, c e d. Gli angoli della figura o vertici Sono indicati in maiuscolo. Infine il angoli interni Sono espressi in lettere greche.
Per definizione, basi di questo trapezio sono i lati aeb, che, come si può vedere, sono paralleli e hanno anche lunghezze diverse.
Il lato perpendicolare a entrambe le basi è il lato c a sinistra, che è il file altezza h del trapezio. E infine c'è il lato d, che forma l'angolo acuto α con il lato a.
La somma dei angoli interni di un quadrilatero è 360º. Si apprezza facilmente che l'angolo mancante C nella figura è 180 - α.
Il base centrale è il segmento che unisce i punti medi dei lati non paralleli (segmento EF in figura 2).
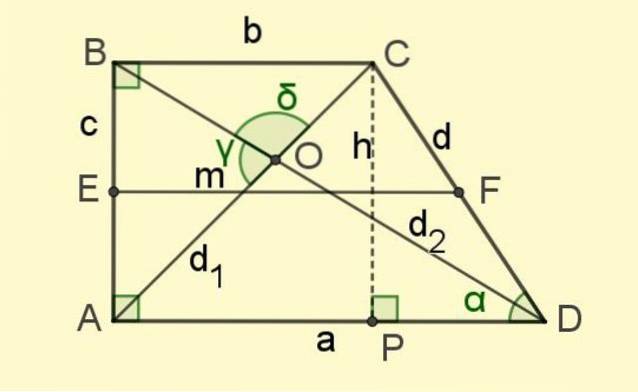
E infine ci sono le diagonali d1 e dDue, i segmenti che uniscono i vertici opposti e si intersecano nel punto O (vedi figura 2).
Relazioni e formule
Altezza trapezoidale h
h = c
Perimetro P
È la misura del contorno e si calcola sommando i lati:
Perimetro = a + b + c + d
Il lato d è espresso in termini di altezza o di lato c usando il teorema di Pitagora:
d = √ (a-b)Due + cDue
Sostituzione nel perimetro:
P = a + b + c + √ (a-b)Due + cDue
Base centrale
È la semi-somma delle basi:
Base media = (a + b) / 2
A volte la base media si trova espressa in questo modo:
Base media = (Base maggiore + base minore) / 2
La zona
L'area A del trapezio è il prodotto della base media per l'altezza:
A = (Base maggiore + base minore) x altezza / 2
A = (a + b) c / 2
Diagonali, lati e angoli
Nella Figura 2 compaiono diversi triangoli, sia a destra che non a destra. Il teorema di Pitagora può essere applicato a quelli che sono triangoli rettangoli ea quelli che non lo sono, i teoremi del coseno e del seno.
In questo modo si trovano le relazioni tra i lati e tra i lati e gli angoli interni del trapezio..
Triangolo CPA
È un rettangolo, le sue gambe sono uguali e valgono b, mentre l'ipotenusa è la diagonale d1, Quindi:
d1Due = bDue + bDue = 2bDue
Triangolo DAB
È anche un rettangolo, le gambe lo sono per Y c (o anche per Y h) e l'ipotenusa è dDue, così che:
dDueDue = aDue + cDue = aDue + hDue
Triangolo CDA
Poiché questo triangolo non è un triangolo rettangolo, viene applicato il teorema del coseno o anche il teorema del seno.
Secondo il teorema del coseno:
d1Due = aDue + dDue - 2ad cos α
Triangolo CDP
Questo triangolo è un triangolo rettangolo e con i suoi lati si costruiscono i rapporti trigonometrici dell'angolo α:
sin α = h / d
cos α = PD / d
Ma il lato PD = a - b, quindi:
cos α = (a-b) / d → a - b = d cos α
a = b + d cos α
Hai anche:
tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)
Triangolo CBD
In questo triangolo abbiamo l'angolo il cui vertice è in C. Non è segnato in figura, ma all'inizio è stato evidenziato che è 180 - α. Questo triangolo non è un triangolo rettangolo, quindi è possibile applicare il teorema del coseno o il teorema del seno..
Ora, si può facilmente dimostrare che:
sin (180 - α) = sin α
cos (180 - α) = - cos α
Applicando il teorema del coseno:
dDueDue = dDue + bDue - 2db cos (180 - α) = dDue + bDue + 2db cos α
Esempi di trapezi destri
I trapezi e in particolare i trapezi di destra si trovano su molti lati, e talvolta non sempre in forma tangibile. Qui abbiamo diversi esempi:
Il trapezio come elemento di design
Le figure geometriche abbondano nell'architettura di molti edifici, come questa chiesa di New York, che mostra una struttura a forma di trapezio rettangolare.
Allo stesso modo, la forma trapezoidale è frequente nella progettazione di contenitori, contenitori, lame (taglierina o esatto), badge e nel design grafico.

Generatore di onde trapezoidali
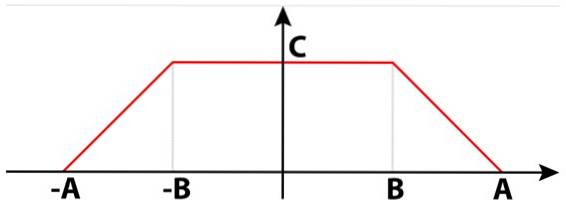
I segnali elettrici non possono essere solo quadrati, sinusoidali o triangolari. Esistono anche segnali trapezoidali utili in molti circuiti. Nella figura 4 è presente un segnale trapezoidale composto da due trapezi destri. Tra di loro formano un singolo trapezio isoscele.
Nel calcolo numerico
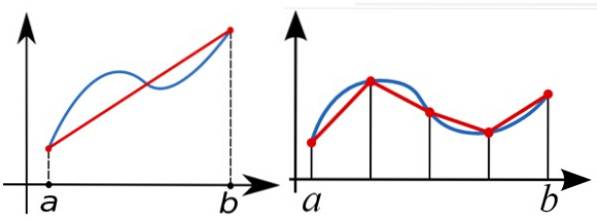
Per calcolare numericamente l'integrale definito della funzione f (x) tra aeb, la regola del trapezio viene utilizzata per approssimare l'area sotto il grafico di f (x). Nella figura seguente, a sinistra l'integrale è approssimato con un unico trapezio destro.
Una migliore approssimazione è quella nella figura a destra, con più trapezi destri.
Trave caricata trapezoidale
Le forze non sono sempre concentrate su un unico punto, poiché i corpi su cui agiscono hanno dimensioni apprezzabili. È il caso di un ponte sul quale circolano continuamente veicoli, l'acqua di una piscina sulle pareti verticali della stessa o un tetto su cui si accumula acqua o neve..
Per questo motivo, le forze sono distribuite per unità di lunghezza, superficie o volume, a seconda del corpo su cui agiscono..
Nel caso di una trave, una forza distribuita per unità di lunghezza può avere varie distribuzioni, ad esempio il trapezio destro mostrato di seguito:
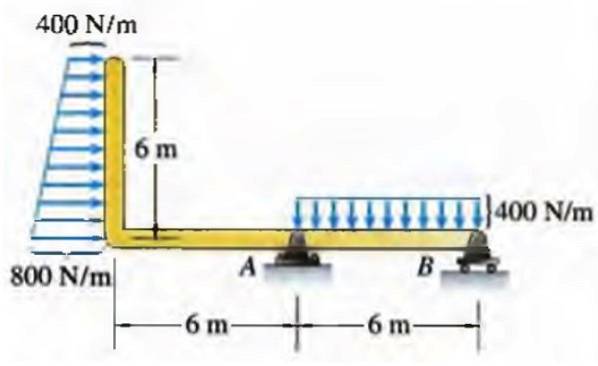
In realtà, le distribuzioni non corrispondono sempre a forme geometriche regolari come questa, ma in molti casi possono essere una buona approssimazione..
Come strumento educativo e di apprendimento
Blocchi e immagini con forme geometriche, compresi i trapezi, sono molto utili affinché i bambini acquisiscano familiarità con l'affascinante mondo della geometria sin dalla tenera età.

Esercizi risolti
- Esercizio 1
Nel trapezio di destra di figura 1, la base più grande è di 50 cm e la base più piccola è pari a 30 cm, è anche noto che il lato obliquo è di 35 cm. Trova:
a) Angolo α
b) Altezza
c) Perimetro
d) Base media
e) Area
f) Diagonali
Soluzione a
I dati del rendiconto sono riassunti come segue:
a = base maggiore = 50 cm
b = base più piccola = 30 cm
d = lato inclinato = 35 cm
Per trovare l'angolo α visitiamo la sezione formule ed equazioni per vedere quale si adatta meglio ai dati forniti. L'angolo cercato si trova in molti dei triangoli analizzati, ad esempio il CDP.
Lì abbiamo questa formula, che contiene l'ignoto e anche i dati che conosciamo:
cos α = (a-b) / d
Perciò:
α = archi [(a-b) / d] = archi [(50-30) / 35] = archi 20/35 = 55,15 º
Soluzione b
Dall'equazione:
sin α = h / d
Cancella h:
h = d. sin α = 35 sin 55,15 º cm = 28,72 cm
Soluzione c
Il perimetro è la somma dei lati, e poiché l'altezza è uguale al lato c, abbiamo:
c = h = 28,72 cm
Perciò:
P = (50 + 30 + 35 + 28,72) cm = 143,72 cm
Soluzione d
La base media è la semi-somma delle basi:
Base centrale = (50 + 30 cm) / 2 = 40 cm
Soluzione e
L'area del trapezio è:
A = base media x altezza = 40 cm x 28,72 = 1148,8 cmDue.
Soluzione f
Per la diagonale d1 puoi usare questa formula:
d1Due = bDue + bDue = 2bDue
d1Due= 2 x (30 cm)Due = 1800 cmDue
d1 = √1800 cmDue = 42,42 cm
E per la diagonale dDue:
dDueDue = dDue + bDue + 2db cos α = (35 cm)Due + (30 cm)Due + 2 x 35 x 30 cmDue cos 55,15 º = 3325 cmDue
dDue = √ 3325 cmDue = 57,66 cm
Questo non è l'unico modo per trovare dDue, poiché c'è anche il triangolo DAB.
- Esercizio 2
Il grafico seguente della velocità in funzione del tempo appartiene a un mobile che ha un moto rettilineo uniformemente accelerato. Calcola la distanza percorsa dal cellulare durante l'intervallo di tempo compreso tra 0,5 e 1,2 secondi.
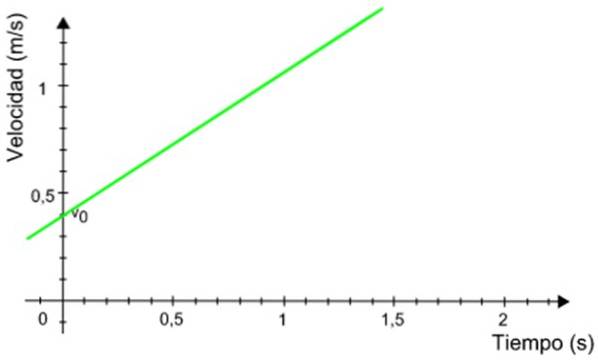
Soluzione
La distanza percorsa dal cellulare è numericamente equivalente all'area sotto il grafico, delimitata dall'intervallo di tempo indicato.
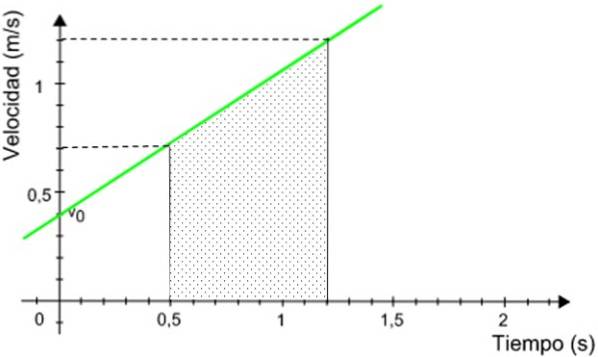
L'area ombreggiata è l'area di un trapezio destro, data da:
A = (Base maggiore + base minore) x altezza / 2
A = (1,2 + 0,7) m / s x (1,2 - 0,5) s / 2 = 0,665 m
Riferimenti
- Baldor, A. 2004. Geometria del piano e dello spazio con la trigonometria. Pubblicazioni culturali.
- Bedford, A. 1996. Statics. Addison Wesley Interamericana.
- Jr. geometria. 2014. Poligoni. Lulu Press, Inc.
- OnlineMSchool. Trapezio rettangolare. Estratto da: es.onlinemschool.com.
- Risolutore automatico di problemi di geometria. Il trapezio. Estratto da: scuolaelettrica.it
- Wikipedia. Trapezoidale (geometria). Estratto da: es.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.