
Dimostrazione del teorema di esistenza e unicità, esempi ed esercizi
Il Teorema di esistenza e unicità stabilisce le condizioni necessarie e sufficienti affinché un'equazione differenziale del primo ordine, con una data condizione iniziale, abbia una soluzione e che questa soluzione sia anche l'unica.
Tuttavia, il teorema non fornisce alcuna tecnica o indicazione su come trovare una tale soluzione. Il teorema di esistenza e unicità è esteso anche alle equazioni differenziali di ordine superiore con condizioni iniziali, noto come problema di Cauchy..
La dichiarazione formale del teorema di esistenza e unicità è la seguente:
"Per un'equazione differenziale y '(x) = f (x, y) con la condizione iniziale y (a) = b, esiste almeno una soluzione in una regione rettangolare del piano XY contenendo al punto (a, b), sì f (x, y) è continuo in quella regione. E se la derivata parziale di F nel rispetto di Y: g = ∂f / ∂e è continuo in quella stessa regione rettangolare, quindi la soluzione è unica in un quartiere del punto (a, b) contenuto nella regione di continuità di F Y g."
L'utilità di questo teorema sta innanzitutto nel sapere quali sono le regioni del piano XY in cui può esistere una soluzione e anche nel sapere se la soluzione trovata è l'unica possibile o se ce ne sono altre..
Si noti che nel caso in cui la condizione di unicità non sia soddisfatta, il teorema non può prevedere quante soluzioni in totale ha il problema di Cauchy: forse è una, due o più.
Indice articolo
- 1 Prova dell'esistenza e teorema di unicità
- 2 esempi
- 2.1 - Esempio 1
- 2.2 - Esempio 2
- 3 esercizi risolti
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 4 Riferimenti
Prova dell'esistenza e teorema di unicità

Per questo teorema sono note due possibili dimostrazioni, una è la dimostrazione di Charles Émile Picard (1856-1941) e l'altra è dovuta a Giuseppe Peano (1858-1932) basata sulle opere di Augustin Louis Cauchy (1789-1857) ).
È interessante notare che le menti matematiche più brillanti del diciannovesimo secolo hanno partecipato alla dimostrazione di questo teorema, quindi si può intuire che nessuna delle due è semplice.
Per dimostrare formalmente il teorema, è necessario prima stabilire una serie di concetti matematici più avanzati, come funzioni di tipo Lipschitz, spazi di Banach, teorema di esistenza di Carathéodory e molti altri, che esulano dallo scopo dell'articolo..
Gran parte delle equazioni differenziali che vengono trattate in fisica si occupano di funzioni continue nelle regioni di interesse, quindi ci limiteremo a mostrare come il teorema viene applicato in equazioni semplici.
Esempi
- Esempio 1
Consideriamo la seguente equazione differenziale con una condizione iniziale:
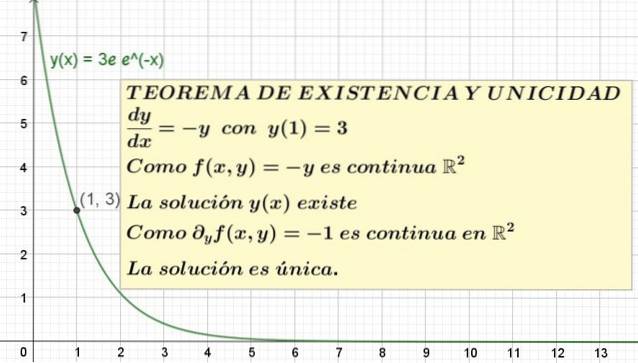
y '(x) = - y; con y (1) = 3
c'è una soluzione per questo problema? È l'unica soluzione possibile?
Risposte
In primo luogo, viene valutata l'esistenza della soluzione dell'equazione differenziale e che soddisfi anche la condizione iniziale.
In questo esempio f (x, y) = - y la condizione dell'esistenza richiede di sapere se f (x, y) è continuo in una regione dell'aereo XY che contiene il punto delle coordinate x = 1, y = 3.
Ma f (x, y) = - y è il funzione affine, che è continuo nel dominio dei numeri reali ed esiste in tutta la gamma dei numeri reali.
Quindi si conclude che f (x, y) è continua in RDue, quindi il teorema garantisce l'esistenza di almeno una soluzione.
Sapendo questo, è necessario valutare se la soluzione è unica o se, al contrario, ce n'è più di una. Per questo è necessario calcolare la derivata parziale di F rispetto alla variabile Y:
∂f / ∂y = ∂ (-y) / ∂y = -1
Poi g (x, y) = -1 che è una funzione costante, che è anche definita per ogni RDue ed è anche continuo lì. Ne consegue che il teorema di esistenza e unicità garantisce che questo problema del valore iniziale abbia una soluzione unica, sebbene non ci dica di cosa si tratta..
- Esempio 2
Considera la seguente equazione differenziale ordinaria del primo ordine con condizione iniziale:
y '(x) = 2√y; y (0) = 0.
C'è una soluzione y (x) per questo problema? In tal caso, determinare se ce n'è uno o più di uno.
Risposta
Consideriamo la funzione f (x, y) = 2√y. La funzione F è definito solo per y≥0, poiché sappiamo che un numero negativo manca di una radice reale. Cosa c'è di più f (x, y) è continuo nel semipiano superiore di RDue compreso l'asse X, quindi il teorema di esistenza e unicità garantisce almeno una soluzione in quella regione.
Ora la condizione iniziale x = 0, y = 0 è sul bordo della regione della soluzione. Quindi prendiamo la derivata parziale di f (x, y) rispetto a y:
∂f/ ∂y = 1 / √y
In questo caso la funzione non è definita per y = 0, proprio dove si trova la condizione iniziale.
Cosa ci dice il teorema? Ci dice che sebbene sappiamo che esiste almeno una soluzione, il semipiano superiore dell'asse X compreso l'asse X, poiché la condizione di unicità non è soddisfatta, non vi è alcuna garanzia che ci sarà una soluzione unica.
Ciò significa che potrebbero esserci una o più soluzioni nella regione di continuità di f (x, y). E come sempre, il teorema non ci dice cosa potrebbero essere.
Esercizi risolti
- Esercizio 1
Risolvi il problema di Cauchy nell'esempio 1:
y '(x) = - y; con y (1) = 3.
Trova la funzione y (x) che soddisfa l'equazione differenziale e la condizione iniziale.
Soluzione
Nell'esempio 1 è stato determinato che questo problema ha una soluzione ed è anche unico. Per trovare la soluzione, la prima cosa da notare è che si tratta di un'equazione differenziale del primo grado di variabili separabili, che si scrive come segue:
dy / dx = - y → dy = -y dx
Dividendo tra e in entrambi i membri per separare le variabili abbiamo:
dy / y = - dx
L'integrale indefinito viene applicato in entrambi i membri:
∫ (1 / y) dy = - ∫dx
Risolvendo gli integrali indefiniti abbiamo:
ln (y) = -x + C
dove C è una costante di integrazione che è determinata dalla condizione iniziale:
ln (3) = -1 + C, ovvero C = 1 + ln (3)
Sostituendo il valore di C e riorganizzandolo rimane:
ln (y) - ln (3) = -x + 1
Applicazione della seguente proprietà dei logaritmi:
La differenza dei logaritmi è il logaritmo del quoziente
L'espressione sopra può essere riscritta in questo modo:
ln (y / 3) = 1 - x
La funzione esponenziale con base e in entrambi i membri viene applicata per ottenere:
y / 3 = e(1 - x)
Che è equivalente a:
y = 3e e-X
Questa è l'unica soluzione dell'equazione y '= -y con y (1) = 3. Il grafico di questa soluzione è mostrato in figura 1.
- Esercizio 2
Trova due soluzioni per il problema posto nell'esempio 2:
y '(x) = 2√ (y); y (0) = 0.
Soluzione
È anche un'equazione di variabili separabili, che, scritta in forma differenziale, si presenta così:
dy / √ (y) = 2 dx
Prendendo l'integrale indefinito in entrambi i membri rimane:
Due √ (y) = 2 x + C
Come fai a saperlo y≥0 nella regione della soluzione abbiamo:
y = (x + C)Due
Ma poiché la condizione iniziale x = 0, y = 0 deve essere soddisfatta, la costante C è zero e rimane la seguente soluzione:
y (x) = xDue.
Ma questa soluzione non è univoca, la funzione y (x) = 0 è anche una soluzione al problema posto. Il teorema di esistenza e unicità applicato a questo problema nell'Esempio 2 aveva già previsto che ci potesse essere più di una soluzione.
Riferimenti
- Coddington, Earl A .; Levinson, Norman (1955), Teoria delle equazioni differenziali ordinarie, New York: McGraw-Hill.
- Enciclopedia della matematica. Teorema di Cauchy-Lipschitz. Estratto da: enciclopediaofmath.org
- Lindelöf, Sur l'application de la méthode des approssimations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Vol.116, 1894, pagg. 454-457. Estratto da: gallica.bnf.fr.
- Wikipedia. Il metodo di approssimazione successiva di Picard. Estratto da: es.wikipedia.com
- Wikipedia. Teorema di Picard-Lindelöf. Estratto da: es.wikipedia.com.
- Zill, D. 1986. Equazioni differenziali elementari con applicazioni Prentice Hall.



Nessun utente ha ancora commentato questo articolo.