UN regola empirica È il risultato dell'esperienza pratica e dell'osservazione della vita reale. Ad esempio, è possibile sapere quali specie di uccelli possono essere osservate in determinati luoghi in ogni periodo dell'anno e da tale osservazione si può stabilire una "regola" che descrive i cicli di vita di questi uccelli.
Nella statistica, la regola empirica si riferisce al modo in cui le osservazioni sono raggruppate attorno a un valore centrale, la media o la media, in unità di deviazione standard..
Supponiamo di avere un gruppo di persone con un'altezza media di 1,62 metri e una deviazione standard di 0,25 metri, allora la regola empirica consentirebbe di definire, ad esempio, quante persone sarebbero in un intervallo della media più o meno uno deviazione standard?
Secondo la regola, il 68% dei dati è più o meno una deviazione standard dalla media, ovvero il 68% delle persone nel gruppo avrà un'altezza compresa tra 1,37 (1,62-0,25) e 1,87 (1,62 + 0,25) metri.
Indice articolo
La regola empirica è una generalizzazione del teorema di Tchebyshev e della distribuzione normale.
Il teorema di Tchebyshev dice che: per qualche valore di k> 1, la probabilità che una variabile casuale cada tra la media meno k volte la deviazione standard e la media più k volte, la deviazione standard è maggiore o uguale a (1 - 1 / KDue).
Il vantaggio di questo teorema è che si applica a variabili aleatorie discrete o continue con qualsiasi distribuzione di probabilità, ma la regola da esso definita non è sempre molto precisa, poiché dipende dalla simmetria della distribuzione. Quanto più distorta è la distribuzione della variabile casuale, tanto meno adattato alla regola sarà il suo comportamento.
La regola empirica definita da questo teorema è:
Se k = √2, si dice che il 50% dei dati si trova nell'intervallo: [µ - √2 s, µ + √2 s]
Se k = 2, si dice che il 75% dei dati si trova nell'intervallo: [µ - 2 s, µ + 2 s]
Se k = 3, si dice che l'89% dei dati si trova nell'intervallo: [µ - 3 s, µ + 3 s]
La distribuzione normale, o campana gaussiana, permette di stabilire la Regola Empirica o Regola 68-95-99,7.
La regola si basa sulle probabilità di occorrenza di una variabile casuale in intervalli tra la media meno una, due o tre deviazioni standard e la media più una, due o tre deviazioni standard..
La regola empirica definisce i seguenti intervalli:
Il 68,27% dei dati si trova nell'intervallo: [µ - s, µ + s]
Il 95,45% dei dati si trova nell'intervallo: [µ - 2s, µ + 2s]
Il 99,73% dei dati si trova nell'intervallo: [µ - 3s, µ + 3s]
Nella figura puoi vedere come vengono presentati questi intervalli e la relazione tra loro quando si aumenta la larghezza della base del grafico.
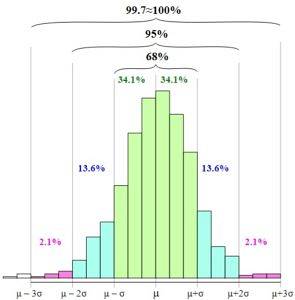
Pertanto, l'applicazione della regola empirica in scala di una variabile normale standard, z, definisce i seguenti intervalli:
Il 68,27% dei dati si trova nell'intervallo: [-1, 1]
Il 95,45% dei dati si trova nell'intervallo: [-2, 2]
Il 99,73% dei dati si trova nell'intervallo: [-3, 3]
La regola empirica consente calcoli abbreviati quando si lavora con una distribuzione normale.
Supponiamo che un gruppo di 100 studenti universitari abbia un'età media di 23 anni, con una deviazione standard di 2 anni. Quali informazioni consente la regola empirica?
L'applicazione della regola empirica comporta i seguenti passaggi:
Poiché la media è 23 e la deviazione standard è 2, gli intervalli sono:
[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]
[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]
[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]
(100) * 68,27% = 68 studenti circa
(100) * 95,45% = 95 studenti circa
(100) * 99,73% = circa 100 studenti
Almeno 68 studenti hanno un'età compresa tra 21 e 25 anni.
Almeno 95 studenti hanno un'età compresa tra 19 e 27 anni.
Quasi 100 studenti hanno tra i 17 ei 29 anni.
La regola empirica è un modo rapido e pratico per analizzare i dati statistici, diventando sempre più affidabile man mano che la distribuzione si avvicina alla simmetria.
La sua utilità dipende dal campo in cui viene utilizzato e dalle domande che vengono presentate. È molto utile sapere che il verificarsi di valori di tre deviazioni standard al di sotto o al di sopra della media è quasi improbabile, anche per variabili di distribuzione non normali, almeno l'88,8% dei casi si trova nell'intervallo di tre sigma.
Nelle scienze sociali, un risultato generalmente conclusivo è l'intervallo della media più o meno due sigma (95%), mentre nella fisica delle particelle, un nuovo effetto richiede un intervallo di cinque sigma (99,99994%) per essere considerato una scoperta..
In una riserva naturale si stima che ci siano una media di 16.000 conigli con una deviazione standard di 500 conigli. Se la distribuzione della variabile "numero di conigli nella riserva" è sconosciuta, è possibile stimare la probabilità che la popolazione di conigli sia compresa tra 15.000 e 17.000 conigli?
L'intervallo può essere presentato in questi termini:
15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s
17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s
Pertanto: [15000, 17000] = [µ - 2 s, µ + 2 s]
Applicando il teorema di Tchebyshev, esiste una probabilità di almeno 0,75 che la popolazione di conigli nella riserva naturale sia compresa tra 15.000 e 17.000 conigli..
Il peso medio dei bambini di un anno in un paese è normalmente distribuito con una media di 10 chilogrammi e una deviazione standard di circa 1 chilogrammo.
a) Stimare la percentuale di bambini di un anno nel paese che hanno un peso medio compreso tra 8 e 12 chilogrammi.
8 = 10 - 2 = 10 - 2 (1) = µ - 2 s
12 = 10 + 2 = 10 + 2 (1) = µ + 2 s
Pertanto: [8, 12] = [µ - 2s, µ + 2s]
Secondo la regola empirica, si può affermare che il 68,27% dei bambini di un anno nel Paese ha tra gli 8 ei 12 chilogrammi di peso.
b) Qual è la probabilità di trovare un bambino di un anno di peso pari o inferiore a 7 chilogrammi?
7 = 10 - 3 = 10 - 3 (1) = µ - 3 s
È noto che 7 chilogrammi di peso rappresenta il valore µ - 3s, così come è noto che il 99,73% dei bambini ha un peso compreso tra 7 e 13 chilogrammi. Ciò lascia solo lo 0,27% del totale dei bambini agli estremi. La metà di loro, lo 0,135%, pesa 7 chilogrammi o meno e l'altra metà, lo 0,135%, pesa 11 chilogrammi o più.
Quindi, si può concludere che esiste una probabilità di 0,00135 che un bambino pesa 7 chilogrammi o meno.
c) Se la popolazione del paese raggiunge i 50 milioni di abitanti ei bambini di 1 anno rappresentano l'1% della popolazione del paese, quanti bambini di un anno peseranno tra i 9 e gli 11 chilogrammi?
9 = 10 - 1 = µ - s
11 = 10 + 1 = µ + s
Pertanto: [9, 11] = [µ - s, µ + s]
Secondo la regola empirica, il 68,27% dei bambini di un anno nel paese si trova nell'intervallo [µ - s, µ + s]
Ci sono 500.000 bambini di un anno nel paese (1% di 50 milioni), quindi 341.350 bambini (68,27% di 500.000) pesano tra i 9 e gli 11 chilogrammi.
Nessun utente ha ancora commentato questo articolo.