
Formula della regola di Simpson, dimostrazione, esempi, esercizi
Il regola dei simpson è un metodo per calcolare, in modo approssimativo, integrali definiti. Si basa sulla divisione dell'intervallo di integrazione in un numero pari di sottointervalli equidistanti.
I valori estremi di due sottointervalli consecutivi definiscono tre punti, per i quali una parabola, la cui equazione è un polinomio di secondo grado, si adatta.
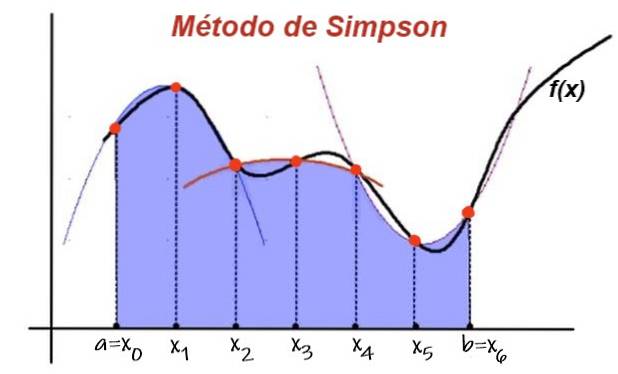
Quindi l'area sotto la curva della funzione nei due intervalli consecutivi viene approssimata dall'area del polinomio di interpolazione. Sommando il contributo all'area sotto la parabola di tutti i successivi sottointervalli, si ha il valore approssimativo dell'integrale.
D'altra parte, poiché l'integrale di una parabola può essere calcolato esattamente algebricamente, è possibile trovare una formula analitica per il valore approssimativo dell'integrale definito. È noto come La formula di Simpson.
L'errore del risultato approssimativo così ottenuto diminuisce al crescere del numero di suddivisioni n (dove n è un numero pari).
Di seguito verrà fornita un'espressione che consente di stimare il limite superiore dell'errore di approssimazione all'integrale I, quando è stata effettuata una partizione di n sottointervalli regolari dell'intervallo totale [a, b].
Indice articolo
- 1 Formula
- 2 Demo
- 2.1 Coefficienti del polinomio di interpolazione
- 2.2 Calcolo dell'integrale approssimativo in [Xi, Xi + 2]
- 2.3 Calcolo approssimativo dell'integrale in [a, b]
- 2.4 Errore di approssimazione
- 3 esempi lavorati
- 3.1 - Esempio 1
- 3.2 - Esempio 2
- 3.3 - Esempio 3
- 4 Esercizio proposto
- 5 Riferimenti
Formula
L'intervallo di integrazione [a, b] è suddiviso in n sottointervalli dove n è un numero intero pari. La larghezza di ogni suddivisione sarà:
h = (b - a) / n
In questo modo, sull'intervallo [a, b] viene realizzata la partizione:
X0, X1, X2,…, Xn-1, Xn
Dove X0 = a, X1 = X0 + h, X2 = X0 + 2h,…, Xn-1 = X0 + (n-1) h, Xn = X0 + nh = b.
La formula che permette di calcolare in modo approssimativo l'integrale definito I della funzione continua, e preferibilmente liscia, sull'intervallo [a, b] è:
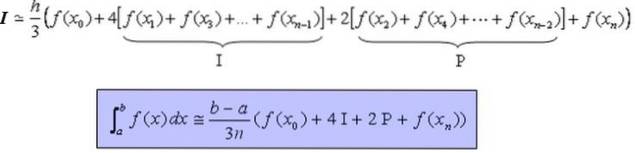
Dimostrazione
Per ottenere la formula di Simpson, in ogni sottointervallo [Xi, Xi + 2] la funzione f (X) è approssimata da un polinomio di secondo grado p (X) (parabola) che passa per i tre punti: [Xi, f (Xi)] ; [Xi + 1, f (Xi + 1)] e [Xi + 2, f (Xi + 2)].
Quindi calcoliamo l'integrale del polinomio p (x) in [Xi, Xi + 2] che approssima l'integrale della funzione f (X) in quell'intervallo.
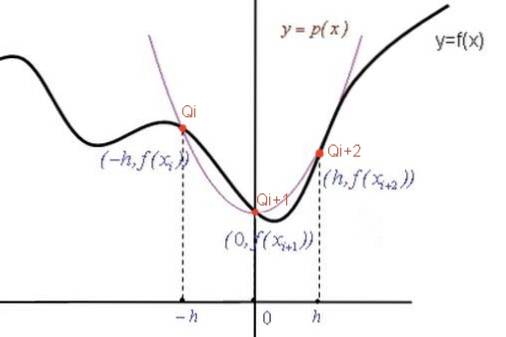
Coefficienti del polinomio di interpolazione
L'equazione della parabola p (X) ha la forma generale: p (X) = A XDue + B X + C.Quando la parabola attraversa i punti Q indicati in rosso (vedi figura), i coefficienti A, B, C sono determinati dal seguente sistema di equazioni:
A (-h)Due - B h + C = f (Xi)
C = f (Xi + 1)
A (h)Due + B h + C = f (Xi + 2)
Si può vedere che il coefficiente C è determinato. Per determinare il coefficiente A aggiungiamo la prima e la terza equazione ottenendo:
2 A hDue + 2 C = f (Xi) + f (Xi + 2).
Quindi il valore di C viene sostituito e A viene cancellato, lasciando:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hDue)
Per determinare il coefficiente B si sottrae la terza equazione dalla prima e si risolve B, ottenendo:
B = [f (Xi + 2) - f (Xi)] = 2 h.
In sintesi, il polinomio di secondo grado p (X) che passa per i punti Qi, Qi + 1 e Qi + 2 ha coefficienti:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hDue)
B = [f (Xi + 2) - f (Xi)] = 2 h
C = f (Xi + 1)
Calcolo dell'integrale approssimativo in [Xi, Xi + 2]
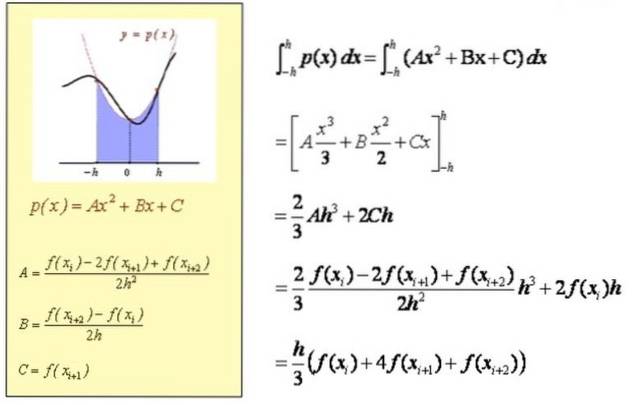
Calcolo approssimativo dell'integrale in [a, b]
Come già accennato, sull'intervallo di integrazione totale [a, b] viene realizzata una partizione X0, X1, X2,…, Xn-1, Xn con passo h = Xi + 1 - Xi = (b - a) / n , dove n è un numero pari.
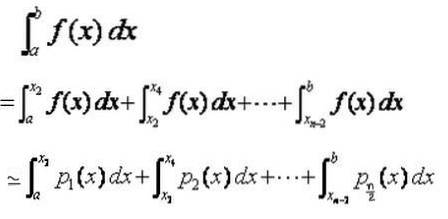
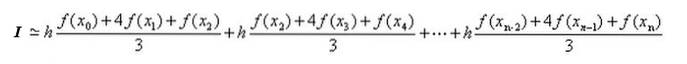
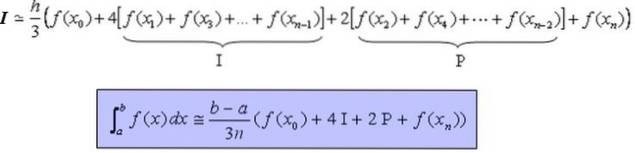
Errore di approssimazione
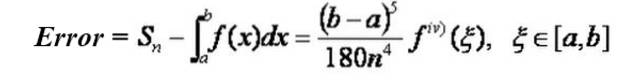
Notare che l'errore diminuisce con la quarta potenza del numero di suddivisioni nell'intervallo. Ad esempio, se passi da n suddivisioni a 2n, l'errore diminuisce di un fattore 1/16.
Il limite superiore dell'errore ottenuto mediante l'approssimazione di Simpson può essere ottenuto da questa stessa formula, sostituendo la quarta derivata al valore massimo assoluto della quarta derivata nell'intervallo [a, b].
Esempi lavorati
- Esempio 1
Considera la funzione la funzione f (X) = 1 / (1 + XDue).
Trova l'integrale definito della funzione f (X) sull'intervallo [-1, 1] usando il metodo di Simpson con due suddivisioni (n = 2).
Soluzione
Prendiamo n = 2. I limiti di integrazione sono a = -1 eb = -2, quindi la partizione ha questo aspetto:
X0 = -1; X1 = 0 e X2 = +1.
Pertanto, la formula di Simpson assume la seguente forma:

Con n = 2 → xo = -1, x1 = 0; x2 = 1, quindi:

- Esempio 2
Considera la funzione f (X) = 1 / (1 + XDue).
Trova l'integrale definito della funzione f (X) sull'intervallo [-1, 1] usando la formula di Simpson con quattro suddivisioni (n = 4).
Soluzione
Prendiamo n = 4. I limiti di integrazione sono a = -1 eb = -2, quindi la partizione ha questo aspetto:
X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 e X4 = +1.
La formula di Simpson è affermata in questo modo:
Integrale ≃ [(b -a) / (3 n)] [f (X0) + 4 I + 2 P + f (Xn)]
Per il caso in cui viene applicato, è il seguente:
Integrale ≃ (1 - (1)) / (3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)
Integrale ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666
- Esempio 3
Determina esattamente l'integrale definito degli esempi precedenti e confronta il risultato esatto con quelli ottenuti usando la formula di Simpson negli esempi 1a e 1b.
Soluzione
L'integrale indefinito della funzione f (X) = 1 / (1 + XDue) è la funzione arctan (X).
Quando si valuta nei limiti dell'integrazione resta:
Integrale = arctan (1) - arctan (-1) = π / 4 - (-π / 4) = π / 2 = 1.5708
Se confrontiamo il risultato della soluzione esatta con quello ottenuto dal metodo di Simpson con n = 2 en = 4, abbiamo:
Per n = 2, la differenza tra la soluzione esatta e quella approssimativa è π / 2 - 5/3 = -0,0959, ovvero una differenza percentuale di -0,06%.
E per l'approssimazione di Simpson con n = 4, la differenza tra la soluzione esatta e quella approssimativa è π / 2-47 / 30 = 0,0041, ovvero una differenza percentuale dello 0,003%.
Esercizio proposto
Il metodo di Simpson è adatto per essere applicato nei linguaggi di programmazione e nelle applicazioni informatiche per calcoli matematici. Si suggerisce al lettore, in base alle formule fornite in questo articolo, di scrivere il proprio codice nel suo programma preferito.
La figura seguente mostra un esercizio in cui è stata implementata la formula di Simpson Studio Smath, software gratuito disponibile per i sistemi operativi finestre Y Android.

Riferimenti
- Casteleiro, J. M. 2002. Calcolo integrale (edizione illustrata). Madrid: editoriale ESIC.
- UPV. Il metodo di Simpson. Politecnico di Valencia. Estratto da: youtube.com
- Purcell, E. 2007. Calculus Ninth Edition. Prentice Hall.
- Wikipedia. La regola di Simpson. Estratto da: es.wikipedia.com
- Wikipedia. Interpolazione polinomiale di Lagrange. Estratto da: es.wikipedia.com


Nessun utente ha ancora commentato questo articolo.