Il proprietà di uguaglianza si riferiscono alla relazione tra due oggetti matematici, siano essi numeri o variabili. È indicato dal simbolo "=", che si trova sempre al centro di questi due oggetti. Questa espressione viene utilizzata per stabilire che due oggetti matematici rappresentano lo stesso oggetto; in altre parole, che due oggetti sono la stessa cosa.
Ci sono casi in cui è banale usare l'uguaglianza. Ad esempio, è chiaro che 2 = 2. Tuttavia, quando si tratta di variabili non è più banale e ha usi specifici. Ad esempio, se abbiamo che y = x e d'altra parte x = 7, possiamo concludere che anche y = 7.
L'esempio sopra si basa su una delle proprietà di uguaglianza, come vedrai a breve. Queste proprietà sono essenziali per risolvere le equazioni (uguaglianze che coinvolgono variabili), che costituiscono una parte molto importante in matematica..
Indice articolo
La proprietà riflessiva, nel caso dell'uguaglianza, afferma che ogni numero è uguale a se stesso ed è espressa come b = b per ogni numero reale b.
Nel caso particolare dell'uguaglianza questa proprietà sembra essere ovvia, ma in altri tipi di relazioni tra numeri non lo è. In altre parole, non tutte le relazioni di numeri reali soddisfano questa proprietà. Ad esempio, un caso del genere della relazione "minore di" (<); ningún número es menor que sí mismo.
La proprietà simmetrica per l'uguaglianza dice che se a = b, allora b = a. Non importa l'ordine utilizzato nelle variabili, sarà preservato dalla relazione di uguaglianza.
Una certa analogia di questa proprietà con la proprietà commutativa può essere osservata nel caso dell'addizione. Ad esempio, a causa di questa proprietà è equivalente a scrivere y = 4 o 4 = y.
La proprietà transitiva sull'uguaglianza afferma che se a = be b = c, allora a = c. Ad esempio, 2 + 7 = 9 e 9 = 6 + 3; quindi, dalla proprietà transitiva abbiamo che 2 + 7 = 6 + 3.
Una semplice applicazione è la seguente: supponiamo che Julian abbia 14 anni e che Mario abbia la stessa età di Rosa. Se Rosa ha la stessa età di Julian, quanti anni ha Mario?
Dietro questo scenario la proprietà transitiva viene utilizzata due volte. Matematicamente viene interpretato così: “a” sia l'età di Mario, “b” l'età di Rosa e “c” l'età di Giuliano. È noto che b = ce che c = 14.
Per la proprietà transitiva abbiamo che b = 14; cioè Rosa ha 14 anni. Poiché a = b e b = 14, usando ancora la proprietà transitiva abbiamo che a = 14; cioè, anche l'età di Mario ha 14 anni.
La proprietà uniforme è che se entrambi i lati di un'uguaglianza vengono aggiunti o moltiplicati per lo stesso importo, l'uguaglianza viene preservata. Ad esempio, se 2 = 2, quindi 2 + 3 = 2 + 3, che è chiaro, poiché 5 = 5. Questa proprietà è particolarmente utile quando si cerca di risolvere un'equazione.
Ad esempio, supponiamo che ti venga chiesto di risolvere l'equazione x-2 = 1. È conveniente ricordare che la risoluzione di un'equazione consiste nel determinare esplicitamente la variabile (o le variabili) coinvolte, sulla base di un numero specifico o di una variabile specificata in precedenza..
Tornando all'equazione x-2 = 1, quello che devi fare è trovare esplicitamente quanto vale x. Per questo, la variabile deve essere cancellata.
È stato erroneamente insegnato che in questo caso, poiché il numero 2 è negativo, passa dall'altra parte dell'uguaglianza con un segno positivo. Ma non è corretto dirlo in questo modo.
Fondamentalmente, quello che stai facendo è applicare la proprietà uniform, come vedremo di seguito. L'idea è di cancellare "x"; vale a dire, lasciarlo da solo su un lato dell'equazione. Per convenzione viene solitamente lasciato sul lato sinistro.
A tal fine, il numero da "eliminare" è -2. Il modo per farlo sarebbe aggiungendo 2, poiché -2 + 2 = 0 e x + 0 = 0. Per poterlo fare senza alterare l'uguaglianza, la stessa operazione deve essere applicata dall'altra parte.
Ciò gli consente di realizzare la proprietà uniforme: poiché x-2 = 1, se il numero 2 viene aggiunto su entrambi i lati dell'uguaglianza, la proprietà uniforme dice che non viene alterata. Allora abbiamo che x-2 + 2 = 1 + 2, che equivale a dire che x = 3. Con questo l'equazione sarebbe risolta.
Allo stesso modo, se vuoi risolvere l'equazione (1/5) y-1 = 9, puoi procedere usando la proprietà uniform come segue:
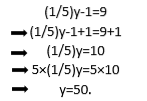
Più in generale, si possono fare le seguenti affermazioni:
- Se a-b = c-b, allora a = c.
- Se x-b = y, allora x = y + b.
- Se (1 / a) z = b, allora z = a ×
- Se (1 / c) a = (1 / c) b, allora a = b.
La proprietà di cancellazione è un caso particolare della proprietà uniforme, considerando in particolare il caso di sottrazione e divisione (che, in sostanza, corrispondono anche all'addizione e alla moltiplicazione). Questa proprietà tratta questo caso separatamente.
Ad esempio, se 7 + 2 = 9, allora 7 = 9-2. O se 2y = 6, allora y = 3 (dividendo per due su entrambi i lati).
Analogamente al caso precedente, tramite la proprietà di cancellazione si possono stabilire le seguenti affermazioni:
- Se a + b = c + b, allora a = c.
- Se x + b = y, allora x = y-b.
- Se az = b, allora z = b / a.
- Se ca = cb, allora a = b.
Se conosciamo il valore di un oggetto matematico, la proprietà di sostituzione afferma che questo valore può essere sostituito in qualsiasi equazione o espressione. Ad esempio, se b = 5 e a = bx, sostituendo il valore di "b" nella seconda uguaglianza abbiamo che a = 5x.
Un altro esempio è il seguente: se "m" divide "n" e anche "n" divide "m", allora deve avere m = n.
Infatti, dire che "m" divide "n" (o equivalentemente, che "m" è un divisore di "n") significa che la divisione m ÷ n è esatta; cioè, dividendo "m" per "n" si ottiene un numero intero, non un decimale. Questo può essere espresso dicendo che esiste un intero "k" tale che m = k × n.
Poiché "n" divide anche "m", allora esiste un intero "p" tale che n = p × m. A causa della proprietà di sostituzione, abbiamo che n = p × k × n, e perché ciò avvenga ci sono due possibilità: n = 0, nel qual caso avremmo l'identità 0 = 0; oppure p × k = 1, da cui l'identità n = n.
Supponiamo che "n" sia diverso da zero. Allora necessariamente p × k = 1; quindi, p = 1 ek = 1. Usando di nuovo la proprietà di sostituzione, quando si sostituisce k = 1 nell'uguaglianza m = k × n (o equivalentemente, p = 1 in n = p × m) otteniamo infine che m = n, che era ciò che volevamo dimostrare.
Proprio come in precedenza si è visto che se un'operazione come addizione, moltiplicazione, sottrazione o divisione viene eseguita in entrambi i termini di un'uguaglianza, viene preservata, allo stesso modo possono essere applicate altre operazioni che non alterano un'uguaglianza.
La chiave è eseguirlo sempre su entrambi i lati dell'uguaglianza e assicurarsi in anticipo che l'operazione possa essere eseguita. Questo è il caso dell'empowerment; cioè, se entrambi i lati di un'equazione sono elevati alla stessa potenza, abbiamo ancora un'uguaglianza.
Ad esempio, poiché 3 = 3, quindi 3Due= 3Due (9 = 9). In generale, dato un intero "n", se x = y, allora xn= en.
Questo è un caso particolare di empowerment e viene applicato quando la potenza è un numero razionale non intero, come ½, che rappresenta la radice quadrata. Questa proprietà afferma che se la stessa radice viene applicata a entrambi i lati di un'uguaglianza (quando possibile), l'uguaglianza viene preservata.
A differenza del caso precedente, qui bisogna fare attenzione alla parità della radice da applicare, poiché è noto che la radice pari di un numero negativo non è ben definita.
Nel caso in cui il radicale sia pari, non ci sono problemi. Ad esempio, se x3= -8, anche se è un'uguaglianza, non è possibile applicare una radice quadrata a entrambi i lati, ad esempio. Tuttavia, se puoi applicare una radice cubica (cosa ancora più conveniente se vuoi conoscere esplicitamente il valore di x), ottenendo così che x = -2.
Nessun utente ha ancora commentato questo articolo.