
Formule di ortoedro, area, volume, diagonale, esempi
Il ortoedro È una figura geometrica volumetrica o tridimensionale che si caratterizza per avere sei facce rettangolari, in modo che le facce opposte siano su piani paralleli e siano rettangoli identici o congruenti. D'altra parte, le facce adiacenti a una data faccia sono in piani perpendicolari a quella della faccia iniziale..
Può anche essere considerato ortoedro come un prisma ortogonale a base rettangolare, in cui il angoli diedri formate dai piani di due facce adiacenti a un bordo comune, misurano 90º. L'angolo diedro tra due facce viene misurato sull'intersezione delle facce con un piano perpendicolare ad esse comune.
Allo stesso modo, l'ortoedro è a parallelepipedo rettangolo, poiché è così che il parallelepipedo viene definito come la figura volumetrica di sei facce, parallele a due a due.
In ogni parallelepipedo le facce sono parallelogrammi, ma nel parallelepipedo rettangolare le facce devono essere rettangolari.
Indice articolo
- 1 Parti dell'ortoedro
- 2 formule di ortoedro
- 2.1 Area
- 2.2 Volume
- 2.3 Diagonale interna
- 3 esempi
- 3.1 - Esempio 1
- 3.2 - Esercizio 2
- 4 Riferimenti
Parti dell'ortoedro
Le parti di un poliedro, come l'ortoedro, Sono:
-Bordi
-Vertici
-Facce
L'angolo tra due bordi di una faccia dell'ortoedro coincide con l'angolo diedro formato dalle sue altre due facce adiacenti a ciascuno dei bordi, formando un angolo retto. L'immagine seguente chiarisce ogni concetto:
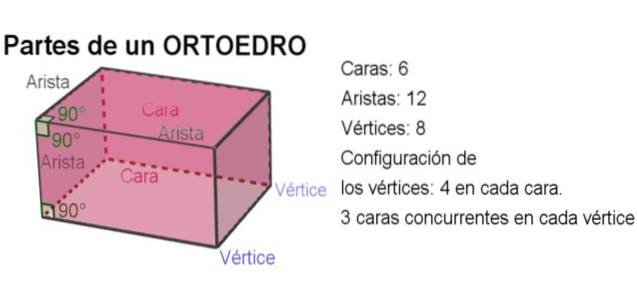
-In totale, un ortoedro ha 6 facce, 12 bordi e 8 vertici..
-L'angolo tra due bordi qualsiasi è un angolo retto.
-Anche l'angolo diedro tra due facce è corretto.
-In ogni faccia ci sono quattro vertici e in ogni vertice concorrono tre facce mutuamente ortogonali.
Formule di ortoedro
La zona
La superficie o l'area di un file ortoedro è la somma delle aree dei loro volti.
Se i tre bordi che si incontrano in un vertice hanno misure a, bec, come mostrato nella Figura 3, la faccia anteriore ha un'area c⋅b e la faccia inferiore ha anche l'area c⋅b.
Quindi le due facce laterali hanno area a⋅b ogni. Infine, le facce del pavimento e del soffitto hanno un'area AVANTI CRISTO ogni.
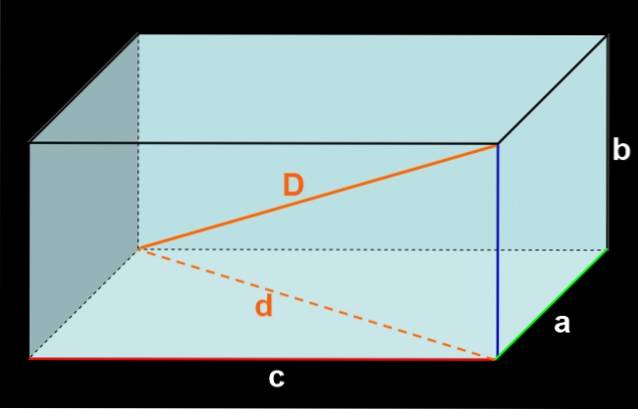
Aggiungendo l'area di tutte le facce si ottiene:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
Prendendo un fattore comune e ordinando i termini:
A = 2⋅ (a⋅b + b⋅c + c⋅a)
Volume
Se l'ortoedro è pensato come un prisma, il suo volume viene calcolato come segue:
Volume = Area della base del prisma x l'altezza del prisma
In questo caso, il pavimento delle dimensioni viene preso come base rettangolare c Y per, allora l'area della base è c⋅a.
L'altezza è data dalla lunghezza b dai bordi ortogonali alle facce laterali per Y c.
Moltiplicando l'area della base (AVANTI CRISTO) per altezza b hai il volume V dell'ortoedro:
V = a⋅b⋅c
Diagonale interna
In un ortoedro ci sono due tipi di diagonali: le diagonali esterne e le diagonali interne.
Le diagonali esterne sono sulle facce rettangolari, mentre le diagonali interne sono i segmenti che uniscono due vertici opposti, intendendosi per vertici opposti quelli che non condividono alcun bordo.
In un ortoedro ci sono quattro diagonali interne, tutte di uguale misura. La lunghezza delle diagonali interne può essere ottenuta applicando il teorema di Pitagora per i triangoli rettangoli.
La lunghezza d della diagonale esterna della faccia del pavimento dell'ortoedro soddisfa la relazione pitagorica:
dDue = aDue + cDue
Allo stesso modo, la diagonale interna della misura D soddisfa la relazione pitagorica:
DDue = dDue + bDue.
Combinando le due espressioni precedenti abbiamo:
DDue = aDue + cDue + bDue.
Infine la lunghezza di una qualsiasi delle diagonali interne dell'ortoedro è data dalla seguente formula:
D = √ (aDue + bDue + cDue ).
Esempi
- Esempio 1
Un muratore costruisce una vasca a forma di ortoedro le cui dimensioni interne sono: 6 m x 4 m di base e 2 m di altezza. Chiede:
a) Determinare la superficie interna del serbatoio se è completamente aperto nella parte superiore.
b) Calcolare il volume dello spazio interno del serbatoio.
c) Trova la lunghezza di una diagonale interna.
d) Qual è la capacità del serbatoio in litri?
Soluzione a
Prenderemo le dimensioni della base rettangolare a = 4 me c = 6 me l'altezza come b = 2 m
L'area di un ortoedro con le dimensioni date è data dalla seguente relazione:
A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
Vale a dire:
A = 2⋅ (8 mDue + 12 mDue + 24 mDue) = 2⋅ (44 mDue) = 88 mDue
Il risultato precedente è l'area dell'ortoedro chiuso con le dimensioni date, ma poiché si tratta di una vasca completamente scoperta nella sua parte superiore, per ottenere la superficie delle pareti interne della vasca, l'area del coperchio mancante deve essere sottratto, ovvero:
c⋅a = 6 m ⋅ 4 m = 24 mDue.
Infine, la superficie interna della vasca sarà: S = 88 mDue - 24 mDue = 64 mDue.
Soluzione b
Il volume interno del serbatoio è dato dal volume di un ortoedro delle dimensioni interne del serbatoio:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Soluzione c
La diagonale interna di un ottaedro con le dimensioni dell'interno della vasca ha una lunghezza D data da:
√ (aDue + bDue + cDue ) = √ ((4 m)Due + (2 m)Due + (6 m)Due )
Effettuando le operazioni indicate abbiamo:
D = √ (16 mDue + 4 mDue + 36 mDue ) = √ (56 mDue) = 2√ (14) m = 7,48 m.
Soluzione d
Per calcolare la capacità del serbatoio in litri, è necessario sapere che il volume di un decimetro cubo è uguale alla capacità di un litro. In precedenza era stato calcolato in volume in metri cubi, ma deve essere trasformato in decimetri cubi e poi in litri:
V = 48 m3 = 48 (10 dm)3 = 4.800 dm3 = 4.800 L
- Esercizio 2
Un acquario di vetro ha una forma cubica con un lato di 25 cm. Determina l'area in mDue, il volume in litri e la lunghezza di una diagonale interna in cm.
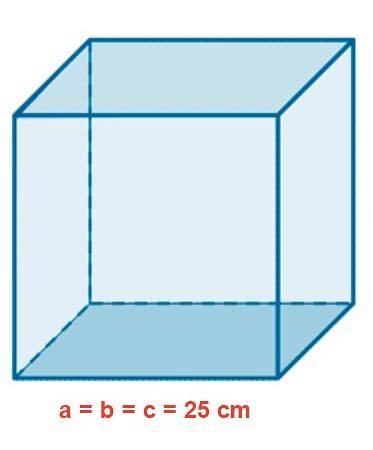
Soluzione
L'area viene calcolata utilizzando la stessa formula dell'ortoedro, ma tenendo conto che tutte le dimensioni sono identiche:
A = 2⋅ (3 a⋅a) = 6⋅ aDue = 6⋅ (25 cm)Due = 1.250 cmDue
Il volume del cubo è dato da:
V = a3 = (25 cm)3 = 15,625 cm3 = 15.625 (0,1 dm)3 = 15.625 dm3 = 15,625 L.
La lunghezza D della diagonale interna è:
D = √ (3aDue) = 25√ (3) cm = 43,30 cm.
Riferimenti
- Arias J. GeoGebra: Prism. Estratto da: youtube.com.
- Calculus.cc. Esercizi e problemi risolti di aree e volumi. Estratto da: calculo.cc.
- Salvador R. Piramide + ortoedro con GEOGEBRA (IHM). Estratto da: youtube.com
- Weisstein, Eric. "Orthohedron". MathWorld. Wolfram Research.
- Wikipedia. Orthohedron Estratto da: es.wikipedia.com



Nessun utente ha ancora commentato questo articolo.