
Calcolo matrice inversa ed esercizio risolto
Il Matrice inversa di una data matrice, è la matrice che moltiplicata per i risultati originali nella matrice identità. La matrice inversa è utile per risolvere sistemi di equazioni lineari, da qui l'importanza di saperla calcolare.
Le matrici sono molto utili in fisica, ingegneria e matematica, poiché sono uno strumento compatto per risolvere problemi complessi. L'utilità delle matrici è aumentata quando sono invertibili ed è noto anche il loro inverso.
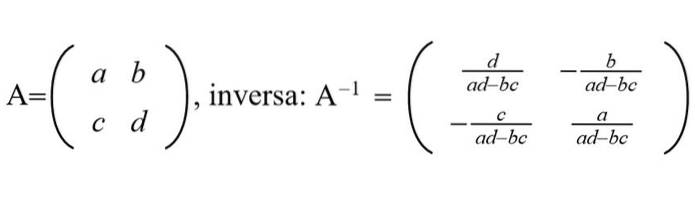
Nei campi dell'elaborazione grafica, Big Data, Data Mining, Machine Learning e altri, vengono utilizzati algoritmi efficienti e veloci per valutare la matrice inversa di matrici nxn con n molto grandi, nell'ordine di migliaia o milioni.
Per illustrare l'uso della matrice inversa nella gestione di un sistema di equazioni lineari, inizieremo con il caso più semplice di tutti: matrici 1 × 1.
Il caso più semplice: si considera un'equazione lineare di una singola variabile: 2 x = 10.
L'idea è di trovare il valore di x, ma sarà fatto "a matrice".
La matrice M = (2) che moltiplica il vettore (x) è una matrice 1 × 1 che risulta nel vettore (10):
M (x) = (10)
L'inverso della matrice M è indicato con M-1.
Il modo generale per scrivere questo "sistema lineare" è:
M X = B, dove X è il vettore (x) e B è il vettore (10).
Per definizione, la matrice inversa è quella che moltiplicata per la matrice originale risulta nella matrice identità I:
M-1 M = I
Nel caso considerato, la matrice M-1 è la matrice (½), cioè M-1 = (½) poiché M-1 M = (½) (2) = (1) = I
Per trovare il vettore sconosciuto X = (x), nell'equazione proposta, entrambi i membri vengono moltiplicati per la matrice inversa:
M-1 M (x) = M-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
È stata raggiunta l'uguaglianza di due vettori, che sono uguali solo quando i loro elementi corrispondenti sono uguali, cioè x = 5.
Calcolo dell'inverso di una matrice
Ciò che motiva il calcolo della matrice inversa è trovare un metodo universale per la soluzione di sistemi lineari come il seguente sistema 2 × 2:
x - 2 y = 3
-x + y = -2
Seguendo i passaggi del caso 1 × 1, studiato nella sezione precedente, scriviamo il sistema di equazioni in forma matriciale:
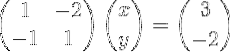
Notare che questo sistema è scritto in notazione vettoriale compatta come segue:
M X = B
dove
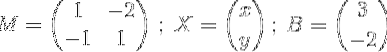
Il prossimo passo è trovare l'inverso di M.
Metodo 1: utilizzo dell'eliminazione gaussiana
Verrà applicato il metodo di eliminazione gaussiana. Che consiste nel fare operazioni elementari sulle righe della matrice, queste operazioni sono:
- Moltiplica una riga per un numero diverso da zero.
- Aggiungi o sottrai da una riga un'altra riga o il multiplo di un'altra riga.
- Scambia le righe.
L'obiettivo è, attraverso queste operazioni, convertire la matrice originaria nella matrice identità.
Fatto ciò, nella matrice M vengono applicate esattamente le stesse operazioni alla matrice identità. Quando dopo diverse operazioni sulle righe M viene trasformata nella matrice unitaria, quella che era originariamente l'unità verrà trasformata nella matrice inversa di M, ovvero M-1.
1- Iniziamo il processo scrivendo la matrice M e accanto ad essa la matrice unitaria:
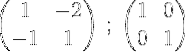
2- Aggiungiamo le due righe e mettiamo il risultato nella seconda riga, in questo modo otteniamo uno zero nel primo elemento della seconda riga:
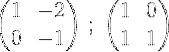
3- Moltiplichiamo la seconda riga per -1 per ottenere 0 e 1 nella seconda riga:
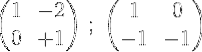
4- La prima riga viene moltiplicata per ½:
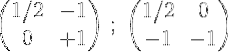
5- Vengono aggiunti il secondo e il primo e il risultato viene posizionato nella prima riga:
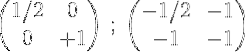
6- Per terminare il processo, moltiplicare la prima riga per 2 per ottenere la matrice identità nella prima riga e la matrice inversa della matrice originale M nella seconda:
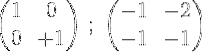
Vale a dire:
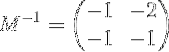
Soluzione di sistema
Una volta ottenuta la matrice inversa, si procede a risolvere il sistema di equazioni applicando la matrice inversa ad entrambi i membri dell'equazione vettoriale compatta:
M-1M X = M-1B
X = M-1B
Che assomiglia esplicitamente a questo:
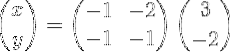
Quindi viene eseguita la moltiplicazione della matrice per ottenere il vettore X:
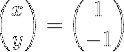
Metodo 2: utilizzo della matrice allegata
In questo secondo metodo si calcola la matrice inversa partendo dalla matrice adiacente della matrice originaria PER.
Supponiamo una matrice A data da:

doveio, j è l'elemento della riga io e la colonna j della matrice PER.
L'aggiunto della matrice PER sarà chiamato Agg. (A) ei suoi elementi sono:
anno Dominiio, j = (-1)(i + j) ¦Ai, j¦
dove Ai, j è la matrice minore complementare ottenuta eliminando la riga i e la colonna j dalla matrice originale PER. Le barre ¦ ¦ indicano che il determinante è calcolato, cioè ¦Ai, j¦ è il determinante della matrice minore complementare.
Formula di matrice inversa
La formula per trovare la matrice inversa a partire dalla matrice adiacente della matrice originale è la seguente:
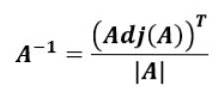
Cioè, la matrice inversa di PER, PER-1, è la trasposizione dell'aggiunto di PER diviso per il determinante di PER.
La trasposizione PERTdi una matrice PER è quella ottenuta scambiando righe per colonne, cioè la prima riga diventa la prima colonna e la seconda riga diventa la seconda colonna e così via fino a quando le n righe della matrice originale non vengono completate.
Esercizio risolto
Sia la matrice A la seguente:
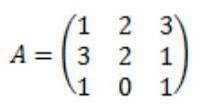
Ogni elemento della matrice aggiunta di A viene calcolato: Adj (A)
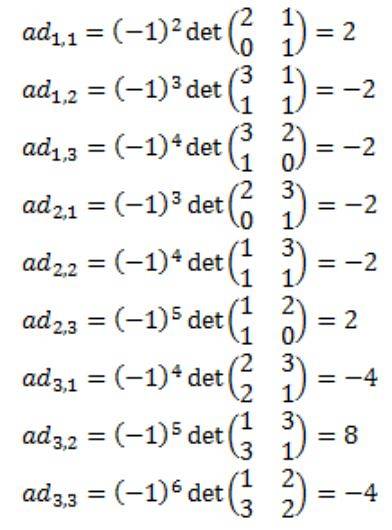
Ne risulta che la matrice aggiunta di A, Adj (A) è la seguente:
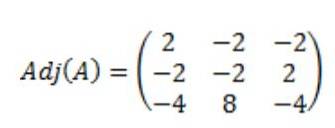
Quindi viene calcolato il determinante della matrice A, det (A):
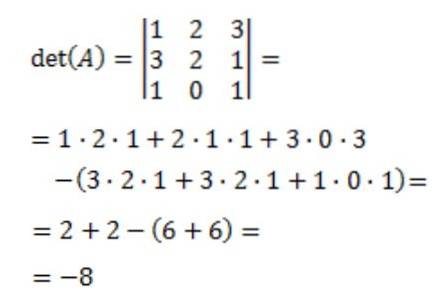
Infine si ottiene la matrice inversa di A:
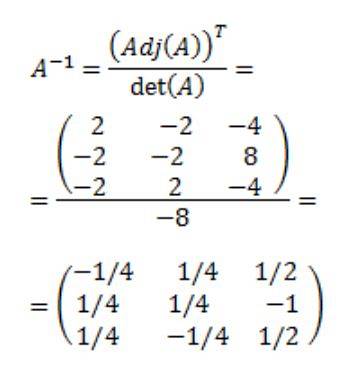
Riferimenti
- Anthony Nicolaides (1994) Determinants & Matrices. Passa la pubblicazione.
- Awol Assen (2013) A Study on the Computation of the Determinants of a 3 × 3
- Casteleiro Villalba M. (2004) Introduzione all'algebra lineare. Editoriale ESIC.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most-Expanding Theories in Mathematics. Ivy press limited.
- Matrice. Pubblicazione accademica di Lap Lambert.


Nessun utente ha ancora commentato questo articolo.