Il decomposizione additiva di un numero intero positivo significa esprimerlo come una somma di due o più numeri interi positivi. Quindi, abbiamo che il numero 5 può essere espresso come 5 = 1 + 4, 5 = 2 + 3 o 5 = 1 + 2 + 2. Ciascuno di questi modi di scrivere il numero 5 è ciò che chiameremo decomposizione additiva.
Se prestiamo attenzione possiamo vedere che le espressioni 5 = 2 + 3 e 5 = 3 + 2 rappresentano la stessa composizione; entrambi hanno lo stesso numero. Tuttavia, solo per comodità, ciascuno degli addendi è solitamente scritto seguendo il criterio dal più basso al più alto.
Indice articolo
Come altro esempio possiamo prendere il numero 27, che possiamo esprimere come:
27 = 7 + 10 + 10
27 = 9 + 9 + 9
27 = 3 + 6 + 9 + 9
27 = 9 + 18
La scomposizione additiva è uno strumento molto utile che ci permette di rafforzare la nostra conoscenza dei sistemi di numerazione.
Quando abbiamo numeri con più di due cifre, un modo particolare per scomporli è nei multipli di 10, 100, 1000, 10 000, ecc., Che lo compongono. Questo modo di scrivere qualsiasi numero è chiamato scomposizione additiva canonica. Ad esempio, il numero 1456 può essere scomposto come segue:
1456 = 1000 + 400+ 50 + 6
Se abbiamo il numero 20846295, la sua decomposizione additiva canonica sarà:
20 846 295 = 20.000.000 + 800.000 + 40.000 + 6000 + 200 + 90 +5.
Grazie a questa scomposizione, possiamo vedere che il valore di una data cifra è dato dalla posizione che occupa. Prendiamo come esempio i numeri 24 e 42:
24 = 20 + 4
42 = 40 +2
Qui possiamo vedere che in 24 il 2 ha un valore di 20 unità e il 4 un valore di 4 unità; in 42 invece il 4 ha un valore di 40 unità e il 2 di due unità. Pertanto, sebbene entrambi i numeri utilizzino le stesse cifre, i loro valori sono completamente diversi a causa della posizione che occupano.
Una delle applicazioni che possiamo dare alla scomposizione additiva è in certi tipi di dimostrazioni, in cui è molto utile vedere un intero positivo come somma di altri.
Prendiamo come esempio il seguente teorema con le sue rispettive dimostrazioni.
- Sia Z un numero intero di 4 cifre, quindi Z è divisibile per 5 se il suo numero di unità è zero o cinque.
Ricordiamo cos'è la divisibilità. Se abbiamo numeri interi "a" e "b", diciamo che "a" divide "b" se esiste un numero intero "c" tale che b = a * c.
Una delle proprietà della divisibilità ci dice che se “a” e “b” sono divisibili per “c”, allora anche la sottrazione “a-b” è divisibile..
Sia Z un numero intero di 4 cifre; quindi possiamo scrivere Z come Z = ABCD.
Usando la scomposizione additiva canonica abbiamo:
Z = A * 1000 + B * 100 + C * 10 + D
È chiaro che A * 1000 + B * 100 + C * 10 è divisibile per 5. Per questo motivo abbiamo che Z è divisibile per 5 se Z - (A * 1000 + B * 100 + C * 10) è divisibile per 5.
Ma Z - (A * 1000 + B * 100 + C * 10) = D e D è un numero a una cifra, quindi l'unico modo per essere divisibile per 5 è che sia 0 o 5.
Pertanto, Z è divisibile per 5 se D = 0 o D = 5.
Nota che se Z ha n cifre la dimostrazione è esattamente la stessa, cambia solo il fatto che ora dovremmo scrivere Z = A1PERDue… PERn e l'obiettivo sarebbe dimostrare che An è zero o cinque.
Diciamo che una partizione di un intero positivo è un modo in cui possiamo scrivere un numero come somma di interi positivi.
La differenza tra una scomposizione additiva e una partizione è che, mentre la prima cerca che almeno possa essere scomposta in due o più addendi, la partizione non ha questa restrizione.
Quindi, abbiamo quanto segue:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 2 + 2
Quelle sopra sono partizioni di 5.
Cioè, abbiamo che ogni decomposizione additiva è una partizione, ma non tutte le partizioni sono necessariamente una decomposizione additiva..
Nella teoria dei numeri, il teorema fondamentale dell'aritmetica garantisce che ogni numero intero può essere scritto in modo univoco come prodotto di numeri primi.
Quando si studiano le partizioni, l'obiettivo è determinare in quanti modi un numero intero positivo può essere scritto come somma di altri numeri interi. Pertanto definiamo la funzione di partizione come presentato di seguito.
La funzione di partizione p (n) è definita come il numero di modi in cui un intero positivo n può essere scritto come somma di interi positivi.
Tornando all'esempio di 5, abbiamo che:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1
Quindi, p (5) = 7.
Sia le partizioni che le scomposizioni additive di un numero n possono essere rappresentate geometricamente. Supponiamo di avere una decomposizione additiva di n. In questa scomposizione gli addendi possono essere disposti in modo che i membri della somma siano ordinati dal minimo al maggiore. Allora va bene:
n = a1 + perDue + per3 +... + Ar con
per1 ≤ aDue ≤ a3 ≤… ≤ ar.
Possiamo rappresentare graficamente questa scomposizione nel modo seguente: in una prima riga contrassegniamo la a1-punti, quindi nel prossimo segniamoDue-punti e così via fino a raggiungere ar.
Prendiamo ad esempio il numero 23 e la sua seguente scomposizione:
23 = 5 + 4 + 7 + 3 + 1 +3
Ordiniamo questa scomposizione e abbiamo:
23 = 1 + 3 + 3 + 4+ 5 + 7
Il suo grafico corrispondente sarebbe:
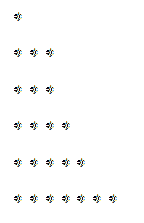
Allo stesso modo, se leggiamo detto grafico verticalmente invece che orizzontalmente, possiamo ottenere una scomposizione possibilmente diversa dalla precedente. Nell'esempio di 23 si distingue quanto segue:
Quindi abbiamo 23 possiamo anche scriverlo come:
23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.
Nessun utente ha ancora commentato questo articolo.