
Proprietà dei vettori liberi, esempi, esercizi
Il vettori liberi Sono quelli che sono pienamente specificati dalla loro grandezza, dalla loro direzione e dal loro senso, senza che sia necessario indicare un punto di applicazione o una particolare origine.
Poiché è possibile disegnare vettori infiniti in questo modo, un vettore libero non è una singola entità, ma un insieme di vettori paralleli e identici che sono indipendenti da dove si trovano..
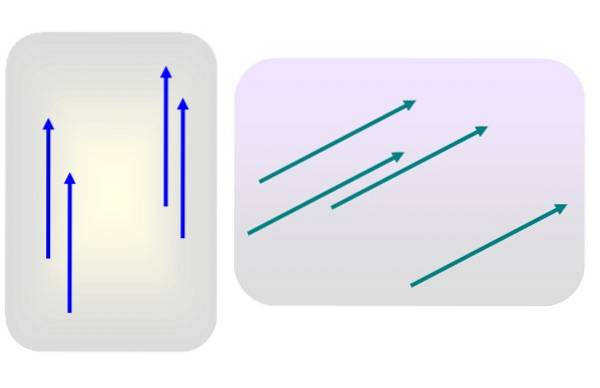
Supponiamo di avere diversi vettori di magnitudine 3 diretti verticalmente verso l'alto, oppure di magnitudine 5 e inclinati verso destra, come in figura 1.
Nessuno di questi vettori viene applicato in modo specifico in qualsiasi punto. Quindi uno qualsiasi dei vettori blu o verdi è rappresentativo del rispettivo gruppo, poiché le loro caratteristiche -modulo, direzione e senso- non cambiano affatto quando vengono trasferiti in un altro punto del piano..
Un vettore libero è solitamente indicato nel testo stampato da una lettera minuscola in grassetto, ad esempio v. O con lettere minuscole e una freccia in alto se si tratta di testo scritto a mano.
Indice articolo
- 1 Esempi
- 1.1 Proprietà e caratteristiche
- 2 Esercizi risolti
- 2.1 -Esercizio 1
- 2.2 Esercizio 2
- 3 Riferimenti
Esempi
Il vantaggio dei vettori liberi è che possono essere spostati attraverso il piano o attraverso lo spazio e mantenere le loro proprietà, poiché qualsiasi rappresentante dell'insieme è ugualmente valido.
Ecco perché in fisica e meccanica sono usati frequentemente. Ad esempio, per indicare la velocità lineare di un solido in movimento, non è necessario scegliere un punto particolare sull'oggetto. Quindi il vettore velocità si comporta come un vettore libero.
Un altro esempio di vettore libero è la coppia di forze. UN paio Consiste di due forze di uguale grandezza e direzione, ma di direzioni opposte, applicate in punti diversi su un solido. L'effetto di una coppia non è quello di traslare l'oggetto, ma di provocare una rotazione grazie al momento prodotto.
La figura 2 mostra una coppia di forze applicate a un volante. Attraverso le forze F1 Y FDue, viene creata una coppia che fa ruotare il volano attorno al suo centro e in senso orario.
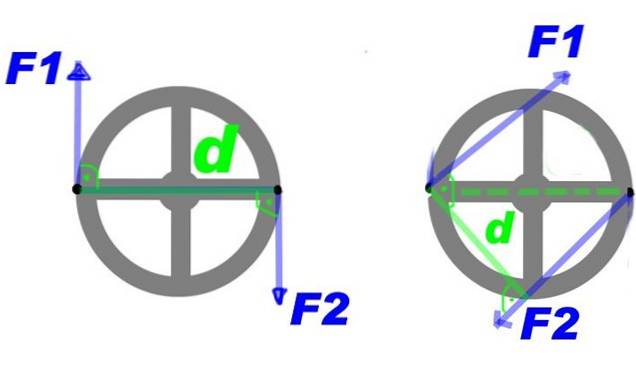
È possibile apportare alcune modifiche alla coppia e ottenere comunque lo stesso effetto di rotazione, ad esempio aumentando la forza, ma diminuendo la distanza tra loro. Oppure mantieni la forza e la distanza, ma applica la coppia su un'altra coppia di punti sul volante, ovvero ruota la coppia attorno al centro.
Il momento della coppia di forze o semplicemente paio, è un vettore il cui modulo è Fd ed è diretto perpendicolare al piano del volano. Nell'esempio mostrato per convenzione la rotazione in senso orario ha senso negativo.
Proprietà e caratteristiche
A differenza del vettore libero v, i vettori AB Y CD sono fissi (vedi figura 3), poiché hanno un punto di partenza e un punto di arrivo specificati. Ma dal momento che sono indulgenti tra loro e, a loro volta, con il vettore v, sono rappresentativi del vettore libero v.

Le proprietà principali dei vettori liberi sono le seguenti:
-Qualsiasi vettore AB (vedi figura 2) è, come detto, rappresentativo del vettore libero v.
-Il modulo, la direzione e il senso sono gli stessi in qualsiasi rappresentante del vettore libero. Nella Figura 2, i vettori AB Y CD rappresentano il vettore libero v e sono orientati al team.
-Dato un punto P nello spazio, è sempre possibile trovare un rappresentante del vettore libero v la cui origine è in P e detto rappresentante è unico. Questa è la proprietà più importante dei vettori liberi e quella che li rende così versatili.
-Un vettore libero nullo è indicato come 0 y è l'insieme di tutti i vettori che mancano di grandezza, direzione e senso.
-Se il vettore AB rappresenta il vettore libero v, poi il vettore BA rappresenta il vettore libero -v.
-Verrà utilizzata la notazione V3 per designare l'insieme di tutti i vettori liberi di spazio e VDue per designare tutti i vettori liberi dell'aereo.
Esercizi risolti
Con i vettori liberi è possibile eseguire le seguenti operazioni:
-Somma
-Sottrazione
-Moltiplicazione di scalare per un vettore
-Prodotto scalare tra due vettori.
-Prodotto incrociato tra due vettori
-Combinazione lineare di vettori
E altro ancora.
-Esercizio 1
Uno studente cerca di nuotare da un punto sulla riva di un fiume a un altro direttamente opposto. Per ottenere ciò, niente direttamente ad una velocità di 6 km / h, in direzione perpendicolare, tuttavia la corrente ha una velocità di 4 km / h che la devia.
Calcola la velocità risultante del nuotatore e quanto viene deviato dalla corrente.
Soluzione
La velocità risultante del nuotatore è la somma vettoriale della sua velocità (rispetto al fiume, tracciata verticalmente verso l'alto) e della velocità del fiume (tracciata da sinistra a destra), che viene effettuata come indicato nella figura sottostante:
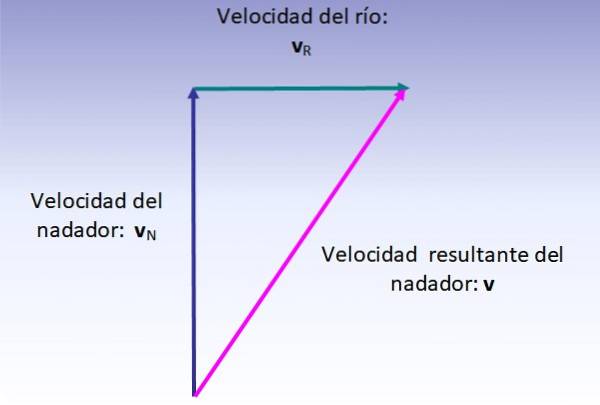
L'entità della velocità risultante corrisponde all'ipotenusa del triangolo rettangolo mostrato, quindi:
v = (6Due + 4Due) ½ km / h = 7,2 km / h
La direzione può essere calcolata utilizzando l'angolo rispetto alla perpendicolare alla riva:
α = arctg (4/6) = 33,7º o 56,3º rispetto alla riva.
Esercizio 2
Trova il momento della coppia mostrato in figura:
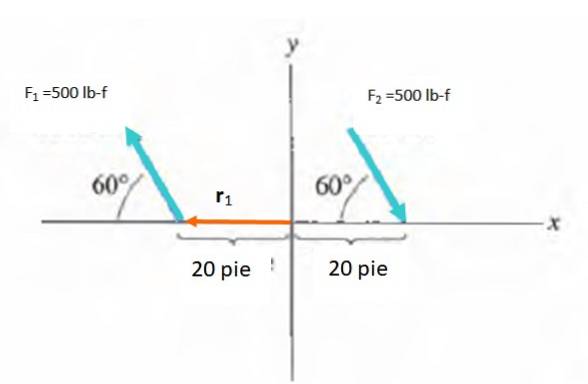
Soluzione
Il momento è calcolato da:
M = r X F
Le unità del momento sono lb-f.ft. Poiché la coppia è nel piano dello schermo, il momento è diretto perpendicolarmente ad esso, verso l'esterno o verso l'interno..
Poiché la coppia nell'esempio tende a ruotare in senso orario l'oggetto su cui è applicato (che non è mostrato in figura), questo momento è considerato puntato verso l'interno dello schermo con segno negativo.
L'intensità del momento è M = F.d. in a, dove a è l'angolo tra la forza e il vettore r. Devi scegliere un punto rispetto al quale calcolare il momento, che è un vettore libero. Viene quindi scelta l'origine del sistema di riferimento r va da O al punto di applicazione di ciascuna forza.
M1 = MDue = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 libbre-f. piede
Il momento netto è la somma di M1 e MDue: -17329,5 libbre-f. piede.
Riferimenti
- Beardon, T. 2011. Un'introduzione ai vettori. Estratto da: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Volume 1. Cinematica. 31-68.
- Fisico. Modulo 8: vettori. Estratto da: frtl.utn.edu.ar
- Hibbeler, R. 2006. Meccanica per ingegneri. Statico. 6a edizione. Continental Publishing Company. 15-53.
- Calcolatrice di addizione vettoriale. Estratto da: 1728.org
- Vettori. Recupero da: en.wikibooks.org



Nessun utente ha ancora commentato questo articolo.