
Calcolo vettoriale di bilanciamento, esempi, esercizi
Il vettore di bilanciamento È quello che si oppone al vettore risultante e quindi è in grado di bilanciare un sistema, poiché ha la stessa grandezza e la stessa direzione, ma la direzione opposta a questa.
In molte occasioni il vettore di bilanciamento si riferisce a un vettore di forza. Per calcolare la forza di bilanciamento, trovare prima la forza risultante, come mostrato nella figura seguente:
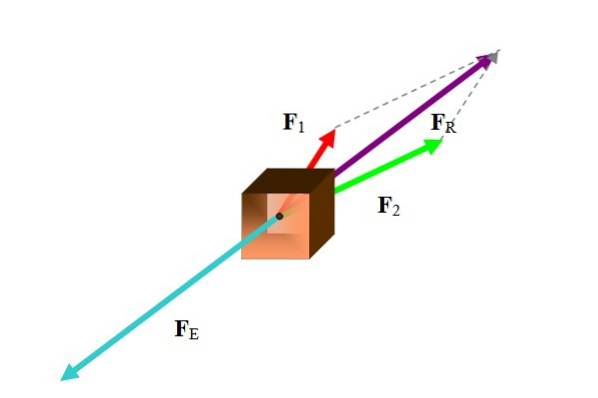
Esistono vari metodi per eseguire questa operazione, a seconda dei dati a portata di mano. Poiché le forze sono vettori, la risultante è la somma vettoriale delle forze partecipanti:
FR = F1 + FDue + F3 + ... .
Tra i metodi da utilizzare ci sono metodi grafici come poligonale, parallelogramma e metodi analitici come la scomposizione delle forze nelle loro componenti cartesiane. Nell'esempio la figura utilizza il metodo del parallelogramma.
Una volta trovata la forza risultante, la forza di bilanciamento è proprio il vettore opposto.
sì FE è la forza di bilanciamento, quindi è soddisfatto che FE applicato in un certo punto, garantisce l'equilibrio traslazionale del sistema. Se è una singola particella, non si muoverà (o forse lo fa con velocità costante), ma se è un oggetto esteso, avrà comunque la capacità di ruotare:
FR + FE = 0
Indice articolo
- 1 Esempi
- 1.1 Tabella delle forze
- 2 Esercizi risolti
- 2.1 -Esercizio 1
- 2.2 -Esercizio 2
- 3 Riferimenti
Esempi
Le forze di bilanciamento sono presenti ovunque. Noi stessi siamo bilanciati dalla forza che la sedia esercita per compensare il peso. Gli oggetti a riposo: libri, mobili, plafoniere e un gran numero di meccanismi, sono continuamente bilanciati dalle forze.
Ad esempio, un libro a riposo su un tavolo è bilanciato dalla normale forza che esercita sul libro, impedendogli di cadere. Lo stesso accade con la catena o il cavo che tiene la lampada appesa al soffitto in una stanza. I cavi che trattengono un carico distribuiscono il loro peso attraverso la tensione al loro interno.
In un fluido alcuni oggetti sono in grado di galleggiare e rimanere a riposo, poiché il loro peso è bilanciato da una forza ascendente esercitata dal liquido, chiamata Spingere.
Vari meccanismi devono essere bilanciati conoscendo il vettore della forza di bilanciamento come barre, travi e colonne.
Quando si utilizza una bilancia, è necessario bilanciare in qualche modo il peso dell'oggetto con una forza equivalente, aggiungendo pesi o mediante molle..
Tabella delle forze
La tabella delle forze viene utilizzata in laboratorio per determinare la forza di bilanciamento. Consiste in una piattaforma circolare, di cui si ha la vista dall'alto in figura, e che ha un goniometro per misurare gli angoli.
Ai bordi del tavolo sono presenti delle carrucole attraverso le quali passano le corde che trattengono i pesi e che convergono in un anello che si trova al centro.
Ad esempio, vengono appesi due pesi. Le tensioni generate nelle corde da questi pesi sono disegnate in rosso e blu in figura 2. Un terzo peso in verde può bilanciare la forza risultante degli altri due e mantenere il sistema in equilibrio..
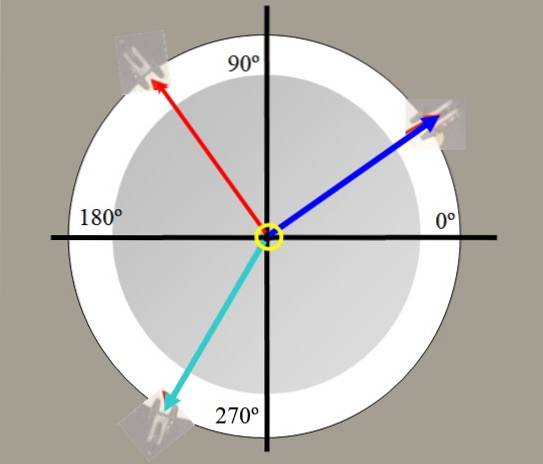
Con la tabella delle forze è possibile verificare il carattere vettoriale delle forze, scomporre le forze, trovare la forza di bilanciamento e verificare il teorema di Lamy:
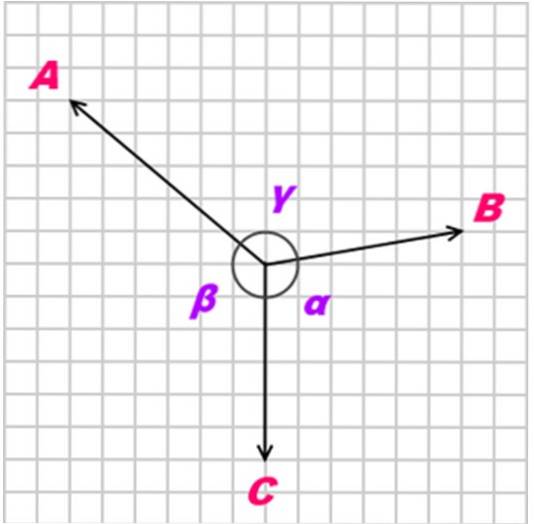
Se un corpo è in equilibrio grazie a tre forze complanari, concorrenti e non collineari (non parallele), chiamate PER, B Y C, la relazione tra queste forze è la seguente:
A / sin α = B / sin β = C / sin γ
Esercizi risolti
-Esercizio 1
I pesi da 225 g (tensione blu) e 150 g (tensione rossa) sono appesi alla tabella delle forze della Figura 2, con gli angoli mostrati. Trova il valore della forza di bilanciamento e l'angolo che fa con l'asse verticale.
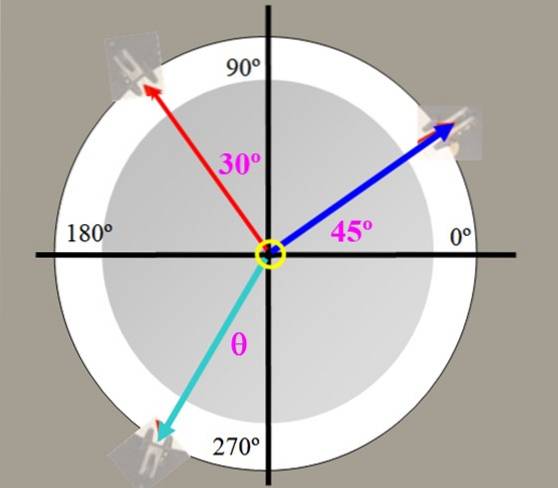
Soluzione
Il problema può essere risolto con i pesi espressi in grammi (forze). Sia P1 = 150 grammi e PDue = 225 grammi, i rispettivi componenti di ciascuno sono:
P1x = 225. cos 45 ° g = 159,10 g; P1y = 225. cos 45º g = 159,10 g
P2x = -150. peccato 30 g = -75,00 g; P2 e = 150. cos 30º g = 129,90 g
Il peso risultante PR si trova aggiungendo algebricamente i componenti:
PRx = 159,10 - 75,00 g = 84,10 g
PRy = 159,10 + 129,90 g = 289,00 g
Il peso di bilanciamento PE è il vettore opposto PR:
PEx = -84,10 g
PHey = -289,00 g
L'entità del peso di equilibratura è calcolata da:
PE = (PExDue + PHeyDue)1/2 = ((-84,10)Due + (-289,00)Due)1/2 g = 301 g
L'angolo θ nella figura è:
θ = arctg (-84,10 / -289,00) = 16,2º rispetto all'asse Y negativo.
-Esercizio 2
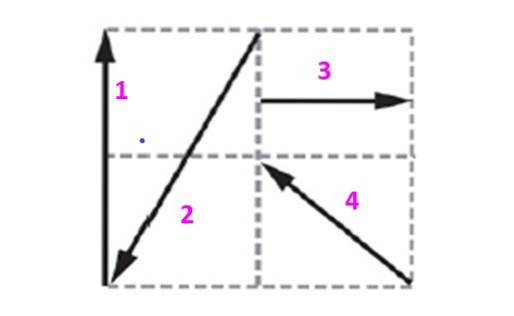
Trova il vettore di bilanciamento del sistema mostrato in figura, sapendo che ogni quadrato misura 10 m di lato.
Soluzione
I vettori contenuti in questa griglia saranno espressi in termini di unità e vettori ortogonali io Y j che determinano l'aereo. Il vettore 1, che sarà indicato come v1 ha magnitudo 20 m ed è diretto verticalmente verso l'alto. Può essere espresso come:
v1 = 0 io +venti j m
Dal disegno si può vedere che il vettore 2 è:
vDue = -10 io - venti j m
Il vettore 3 è orizzontale e punta nella direzione positiva:
v3 = 10 io + 0 j m
Infine il vettore 4 è inclinato di 45º, poiché è la diagonale del quadrato, quindi le sue componenti misurano lo stesso:
v4 = -10 io + 10 j m
Si noti che i segni indicano verso quale lato dell'asse si trovano i componenti: in alto ea destra hanno un segno +, mentre in basso ea sinistra hanno un segno -.
Il vettore risultante si ottiene aggiungendo un componente al componente:
vR = -10 io + 10 j m
Quindi il vettore di bilanciamento del sistema è:
vE = 10 io - 10 j m
Riferimenti
- Beardon, T. 2011. Un'introduzione ai vettori. Estratto da: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Volume 1. Cinematica. 31-68.
- Fisico. Modulo 8: vettori. Estratto da: frtl.utn.edu.ar
- Hibbeler, R. 2006. Meccanica per ingegneri. Statico. 6a edizione. Continental Publishing Company. 15-53.
- Calcolatrice di addizione vettoriale. Estratto da: 1728.org
- Vettori. Recupero da: wikibooks.org

Nessun utente ha ancora commentato questo articolo.