Il cella unitaria È uno spazio o una regione immaginaria che rappresenta l'espressione minima di un tutto; che nel caso della chimica il tutto sarebbe un cristallo composto da atomi, ioni o molecole, che si dispongono secondo uno schema strutturale.
Nella vita di tutti i giorni si possono trovare esempi che incarnano questo concetto. Per questo, è necessario prestare attenzione a oggetti o superfici che esibiscono un certo ordine ripetitivo dei loro elementi. Alcuni mosaici, bassorilievi, soffitti a cassettoni, fogli e carte da parati, possono racchiudere in termini generali quanto si intende per cella unitaria.
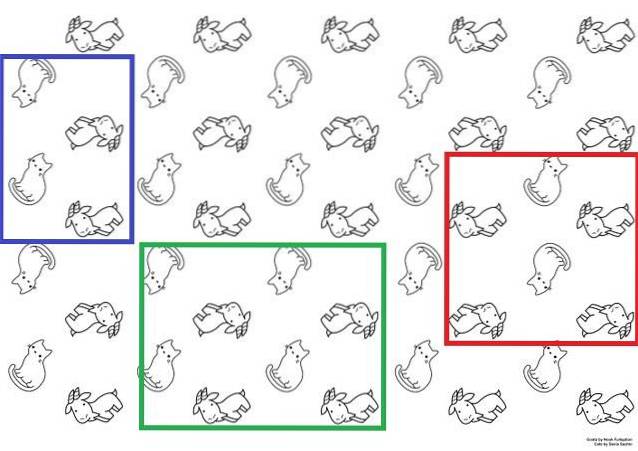
Per illustrarlo più chiaramente, c'è l'immagine sopra che potrebbe essere usata come sfondo. In esso compaiono gatti e capre con due sensi alternativi; i gatti sono in posizione verticale o capovolta e le capre sono sdraiate rivolte verso l'alto o verso il basso.
Questi gatti e capre stabiliscono una sequenza strutturale ripetitiva. Per costruire l'intera carta basterebbe riprodurre la cellula unitaria sulla superficie un numero sufficiente di volte, utilizzando movimenti di traslazione..
Le possibili celle unitarie sono rappresentate dai riquadri blu, verde e rosso. Ognuno di questi tre potrebbe essere utilizzato per ottenere il ruolo; ma è necessario spostarli con fantasia lungo la superficie per scoprire se riproducono la stessa sequenza osservata nell'immagine.
Partendo dal riquadro rosso, si apprezzerebbe che se tre colonne (di gatti e capre) venissero spostate a sinistra, due capre non apparirebbero più in basso ma solo una. Pertanto, porterebbe a un'altra sequenza e non può essere considerata come una cella unitaria.
Se invece spostassero con fantasia le due caselle, blu e verde, si otterrebbe la stessa sequenza del foglio. Entrambi sono celle unitarie; tuttavia, il riquadro blu obbedisce maggiormente alla definizione, poiché è più piccolo del riquadro verde.
Indice articolo
La sua stessa definizione, oltre all'esempio appena spiegato, chiarisce molte delle sue proprietà:
-Se ti muovi nello spazio, indipendentemente dalla direzione, otterrai il solido o il cristallo completo. Questo perché, come accennato con gatti e capre, ne riproducono la sequenza strutturale; che è uguale alla distribuzione spaziale delle unità ripetitive.
-Devono essere il più piccolo possibile (o occupare poco volume) rispetto ad altre possibili opzioni di cella.
-Di solito sono simmetrici. Inoltre, la sua simmetria si riflette letteralmente nei cristalli del composto; se la cella unitaria di un sale è cubica, i suoi cristalli saranno cubici. Tuttavia, ci sono strutture cristalline che sono descritte con celle unitarie con geometrie distorte..
-Contengono unità ripetitive, che possono essere sostituite da punti, che a loro volta compongono ciò che è noto come reticolo in tre dimensioni. Nell'esempio precedente i gatti e le capre rappresentano i punti reticolari, visti da un piano più alto; cioè due dimensioni.
Le unità ripetitive o punti reticolari delle celle unitarie mantengono la stessa proporzione delle particelle solide.
Se conti il numero di gatti e capre nella casella blu, avrai due gatti e due capre. Lo stesso accade con il riquadro verde, e anche con il riquadro rosso (anche se è già noto che non è una cella unitaria).
Supponiamo, ad esempio, che gatti e capre siano rispettivamente atomi di G e C (una strana saldatura animale). Poiché il rapporto tra G e C è 2: 2 o 1: 1 nella casella blu, ci si può tranquillamente aspettare che il solido abbia la formula GC (o CG).
Quando il solido presenta strutture più o meno compatte, come accade con sali, metalli, ossidi, solfuri e leghe, nelle celle unitarie non sono presenti intere unità ripetitive; cioè, ci sono porzioni o parti di esse, che sommano fino a una o due unità.
Questo non è il caso di GC. In tal caso, la casella blu "dividerebbe" i gatti e le capre in due (1 / 2G e 1 / 2C) o quattro (1 / 4G e 1 / 4C). Nelle prossime sezioni si vedrà che in queste celle unitarie i punti reticolari sono opportunamente suddivisi in questo e in altri modi..
Le celle unitarie nell'esempio GC sono bidimensionali; tuttavia, questo non si applica ai modelli reali che considerano tutte e tre le dimensioni. Così, i quadrati o parallelogrammi, si trasformano in parallelepipedi. Ora, il termine "cellula" ha più senso.
Le dimensioni di queste celle o parallelepipedi dipendono dalla lunghezza dei rispettivi lati e angoli..
Nell'immagine inferiore hai l'angolo inferiore posteriore del parallelepipedo, composto dai lati per, b Y c, e gli angoli α, β e γ.
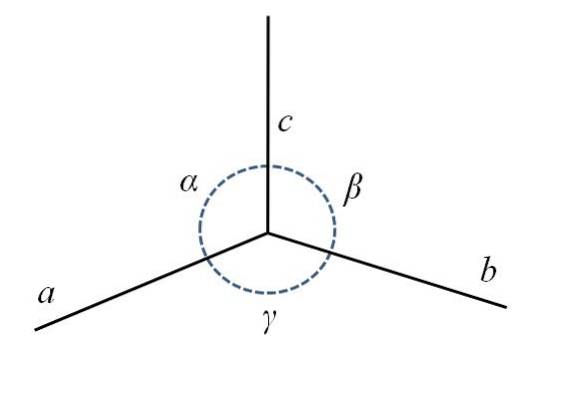
Come potete vedere, per è un po 'più lungo di b Y c. Al centro c'è un cerchio tratteggiato per indicare gli angoli α, β e γ, tra AC, cb Y ba, rispettivamente. Per ogni cella unitaria questi parametri hanno valori costanti e definiscono la sua simmetria e quella del resto del cristallo..
Applicando di nuovo un po 'di immaginazione, i parametri dell'immagine definirebbero una cella simile a un cubo allungata sul bordo. per. Pertanto, le celle unitarie si presentano con lunghezze e angoli diversi dei loro bordi, che possono anche essere classificati in vari tipi.
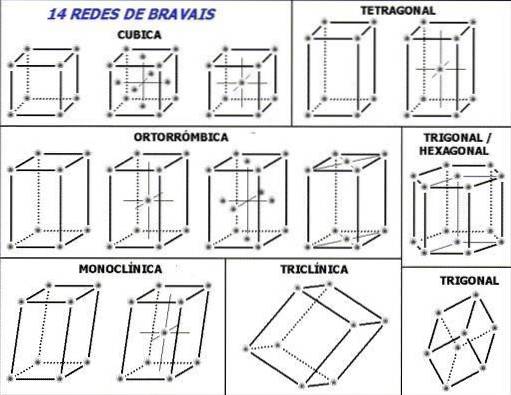
Nota per iniziare nell'immagine in alto le linee tratteggiate all'interno delle celle unitarie: indicano l'angolo posteriore inferiore, come appena spiegato. La seguente domanda può essere posta, dove sono i punti reticolo o le unità ripetitive? Sebbene diano l'impressione sbagliata che le celle siano vuote, la risposta si trova ai vertici.
Queste celle vengono generate o scelte in modo tale che le unità ripetitive (punti grigiastri dell'immagine) si trovino ai loro vertici. A seconda dei valori dei parametri stabiliti nella sezione precedente, costanti per ogni cella unitaria, si ricavano sette sistemi cristallini.
Ogni sistema cristallino ha la sua cella unitaria; il secondo definisce il primo. Nell'immagine in alto ci sono sette quadrati, corrispondenti ai sette sistemi cristallini; o in un modo leggermente più sintetico, reti cristalline. Così, ad esempio, una cella unitaria cubica corrisponde a uno dei sistemi cristallini che definisce un reticolo cristallino cubico.
Secondo l'immagine, i sistemi o le reti cristalline sono:
-Cubo
-Tetragonale
-Ortorombica
-Esagonale
-Monoclinic
-Triclinic
-Trigonale
E all'interno di questi sistemi cristallini ne sorgono altri che compongono le quattordici reti di Bravais; che tra tutte le reti cristalline, sono le più elementari.
In un cubo tutti i suoi lati e angoli sono uguali. Pertanto, in questa cella unitaria è vero quanto segue:
per = b = c
α = β = γ = 90º
Esistono tre celle unitarie cubiche: semplice o primitiva, centrata sul corpo (bcc) e centrata sulla faccia (fcc). Le differenze risiedono nel modo in cui i punti sono distribuiti (atomi, ioni o molecole) e nel numero di essi.
Quale di queste celle è la più compatta? Quello il cui volume è più occupato dai punti: quello cubico centrato sulle facce. Nota che se sostituissimo i punti per i gatti e le capre dall'inizio, non sarebbero confinati in una singola cella; apparterrebbero e sarebbero condivisi da molti. Di nuovo, sarebbero porzioni di G o C.
Se i gatti o le capre fossero ai vertici, sarebbero condivisi da 8 celle unitarie; cioè, ogni cella avrebbe 1/8 di G o C. Unisci o immagina 8 cubi, in due colonne di due righe ciascuna, per visualizzarlo.
Se i gatti o le capre fossero sui volti, sarebbero condivisi solo da 2 celle unitarie. Per vederlo, metti insieme due cubi.
D'altra parte, se il gatto o la capra fossero al centro del cubo, apparterrebbero solo a una singola cella unitaria; Lo stesso accade con le scatole nell'immagine principale, quando il concetto è stato affrontato.
Detto quindi quanto sopra, all'interno di una semplice cella cubica abbiamo un unità o punto reticolare, poiché ha 8 vertici (1/8 x 8 = 1). Per la cella cubica centrata nel corpo ci sono: 8 vertici, che è uguale a un atomo, e un punto o unità al centro; quindi c'è Due unità.
E per la cella cubica centrata sulla faccia ci sono: 8 vertici (1) e sei facce, dove metà di ogni punto o unità è condivisa (1/2 x 6 = 3); quindi, possiede quattro unità.
Commenti simili possono essere fatti riguardo alla cella unitaria per il sistema tetragonale. I suoi parametri strutturali sono i seguenti:
per = b ≠ c
α = β = γ = 90º
I parametri per la cellula ortorombica sono:
per ≠ b ≠ c
α = β = γ = 90º
I parametri per la cellula monoclina sono:
per ≠ b ≠ c
α = γ = 90 °; β ≠ 90º
I parametri per la cella triclina sono:
per ≠ b ≠ c
α ≠ β ≠ γ ≠ 90º
I parametri per la cella esagonale sono:
per = b ≠ c
α = β = 90 °; γ ≠ 120º
In realtà la cella costituisce un terzo di un prisma esagonale.
E infine, i parametri per la cellula trigonale sono:
per = b = c
α = β = γ ≠ 90º
Nessun utente ha ancora commentato questo articolo.