Il triangoli acuti sono quelli i cui tre angoli interni sono angoli acuti; ovvero, la misura di ciascuno di questi angoli è inferiore a 90 ° gradi. Non avendo alcun angolo retto, abbiamo che il teorema di Pitagora non vale per questa figura geometrica.
Pertanto, se vogliamo avere qualche tipo di informazione su uno qualsiasi dei suoi lati o angoli, è necessario fare uso di altri teoremi che ci consentono di avere accesso a tali dati. Quelli che possiamo usare sono il teorema del seno e il teorema del coseno.
Indice articolo
Tra le caratteristiche che possiede questa figura geometrica, possiamo evidenziare quelle che sono date dal semplice fatto di essere un triangolo. Tra questi abbiamo:
- Un triangolo è un poligono che ha tre lati e tre angoli.
- La somma dei suoi tre angoli interni è pari a 180 °.
- La somma di due dei suoi lati è sempre maggiore del terzo.
Ad esempio, diamo un'occhiata al seguente triangolo ABC. In generale, ne identifichiamo i lati con una lettera minuscola e gli angoli con una maiuscola, in modo tale che un lato e il suo angolo opposto abbiano la stessa lettera.
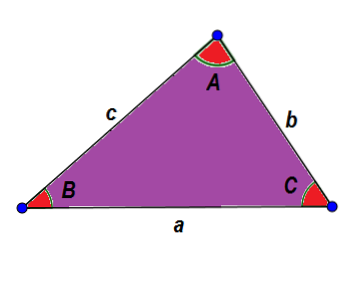
Dalle caratteristiche già riportate sappiamo che:
A + B + C = 180 °
a + b> c, a + c> be b + c> a
La caratteristica principale che distingue questo tipo di triangolo dal resto è che, come abbiamo già accennato, i suoi angoli interni sono acuti; cioè, la misura di ciascuno dei suoi angoli è inferiore a 90 °.
I triangoli acuti, insieme ai triangoli ottusi (quelli in cui uno dei loro angoli ha una misura maggiore di 90 °), fanno parte dell'insieme dei triangoli obliqui. Questo set è composto dai triangoli che non sono angoli retti.
Poiché i triangoli obliqui sono parte, dobbiamo essere in grado di risolvere problemi che coinvolgono triangoli acuti, dobbiamo usare il teorema del seno e il teorema del coseno.
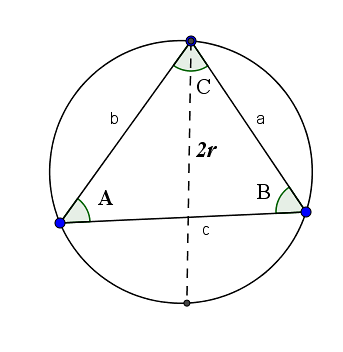
Il teorema del seno ci dice che il rapporto tra un lato e il seno del suo angolo opposto è uguale al doppio del raggio del cerchio formato dai tre vertici di detto triangolo. Vale a dire:
2r = a / sin (A) = b / sin (B) = c / sin (C)
D'altra parte, il teorema del coseno ci fornisce queste tre uguaglianze per ogni triangolo ABC:
perDue= bDue + cDue -2bc * cos (A)
bDue= aDue + cDue -2ac * cos (B)
cDue= aDue + bDue -2ab * cos (C)
Questi teoremi sono noti anche come legge del seno e legge del coseno, rispettivamente..
Un'altra caratteristica che possiamo dare dei triangoli acuti è che due di questi sono uguali se soddisfano uno dei seguenti criteri:
- Se hanno tutti e tre i lati uguali.
- Se hanno un lato e due angoli uguali tra loro.
- Se hanno due lati uguali e un angolo.
Possiamo classificare i triangoli acuti in base ai loro lati. Questi potrebbero essere:
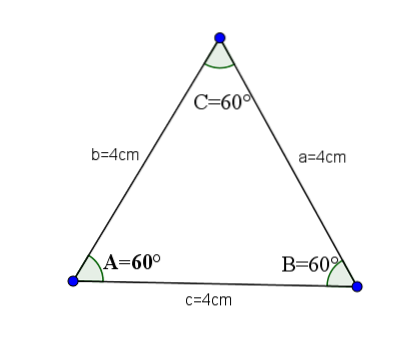
Sono i triangoli acuti che hanno tutti i lati uguali e, quindi, tutti i loro angoli interni hanno lo stesso valore, che è A = B = C = 60 ° gradi.
Ad esempio, prendiamo il triangolo seguente, i cui lati a, bec hanno valore 4.
Questi triangoli, oltre ad avere angoli interni acuti, hanno la caratteristica di avere due dei loro lati uguali e il terzo, che generalmente viene preso come base, diverso.
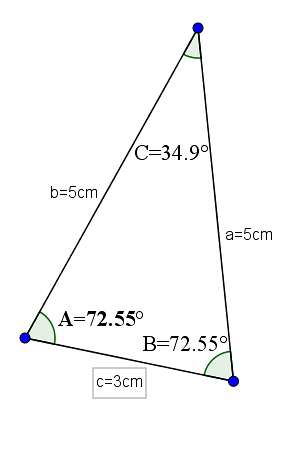
Un esempio di questo tipo di triangolo può essere uno la cui base è 3 e gli altri due lati hanno valore 5. Con queste misurazioni, avrebbe gli angoli opposti ai lati uguali con il valore di 72,55 ° e l'angolo opposto di la base sarebbe 34,9 °.
Questi sono i triangoli che hanno tutti lati diversi a due a due. Pertanto, tutti i suoi angoli, oltre ad essere inferiori a 90 °, sono diversi da due a due.
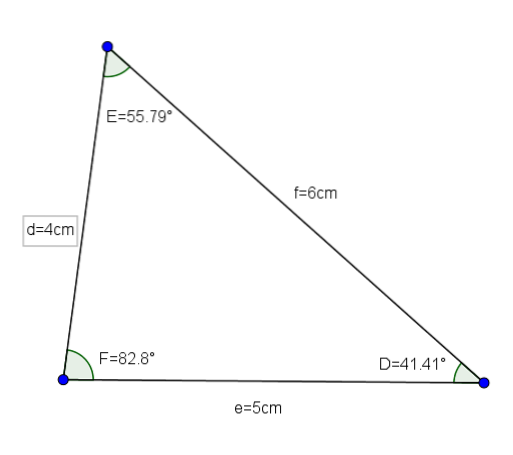
Il triangolo DEF (le cui misure sono d = 4, e = 5 ef = 6 e i suoi angoli sono D = 41,41 °, E = 55,79 ° e F = 82,8 °) è un buon esempio di triangolo acuto scaleno.
Come abbiamo detto prima, per risolvere problemi che coinvolgono i triangoli acuti è necessario utilizzare i teoremi seno e coseno.
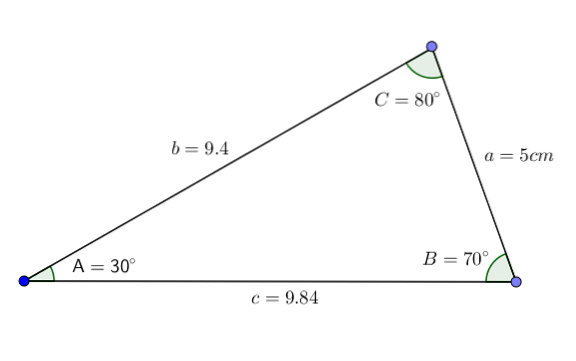
Dato un triangolo ABC con angoli A = 30 °, B = 70 ° e lato a = 5cm, vogliamo conoscere il valore dell'angolo C e dei lati bec.
La prima cosa che facciamo è utilizzare il fatto che la somma degli angoli interni di un triangolo è di 180 °, in modo da ottenere il valore dell'angolo C.
180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C
Cancelliamo C e ci ritroviamo con:
C = 180 ° - 100 ° = 80 °
Poiché conosciamo già i tre angoli e un lato, possiamo usare il teorema del seno per determinare il valore dei lati rimanenti. Per il teorema abbiamo:
a / sin (A) = b / sin (B) e a / sin (A) = c / (sin (C)
Isoliamo b dall'equazione e ci rimane:
b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4
Ora dobbiamo solo calcolare il valore di c. Procediamo come nel caso precedente:
c = (a * sin (C)) / sin (A) ≈ (5 * 0.984) / (0.5) ≈ 9.84
Otteniamo così tutti i dati del triangolo. Come possiamo vedere, questo triangolo rientra nella categoria del triangolo acuto scaleno.
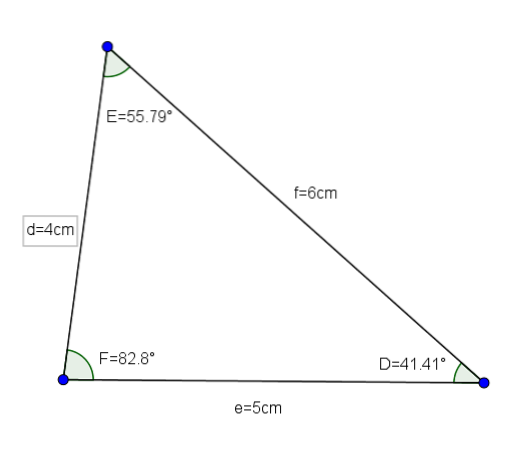
Dato un triangolo DEF con lati d = 4cm, e = 5cm ef = 6cm, vogliamo conoscere il valore degli angoli di detto triangolo.
In questo caso useremo la legge del coseno, che ci dice che:
dDue= eDue + FDue - 2efcos (D)
Da questa equazione possiamo risolvere per cos (D), che ci dà come risultato:
Cos (D) = ((4)Due - (5)Due -(6)Due) / (- 2 * 5 * 6) = 0,75
Quindi abbiamo D≈ 41,41 °
Ora usando il teorema di senom abbiamo la seguente equazione:
d / (sin (D) = e / (sin (E)
Risolvendo per il peccato (E), abbiamo:
sin (E) = e * sin (D) / d = (5 * 0,66) / 4 ≈ 0,827
Quindi abbiamo E≈55,79 °
Infine, usando che la somma degli angoli interni di un triangolo è 180 °, abbiamo quel F≈82,8 °.
Nessun utente ha ancora commentato questo articolo.