Il traiettoria in fisica È la curva che un mobile descrive mentre attraversa punti successivi durante il suo movimento. Poiché può adottare un numero infinito di varianti, lo saranno anche le traiettorie che il mobile potrà seguire.
Per spostarsi da un luogo all'altro, una persona può intraprendere percorsi e modi diversi: a piedi attraverso i marciapiedi di strade e viali, oppure arrivando in macchina o in moto su un'autostrada. Durante una passeggiata nel bosco, il camminatore può seguire un percorso complicato che include curve, salite o discese di livello e anche attraversando più volte lo stesso punto.
Se i punti attraverso i quali il mobile sta viaggiando seguono una linea retta, la traiettoria sarà rettilinea. Questo è il percorso più semplice, perché è unidimensionale. La specifica della posizione richiede una singola coordinata.
Ma il cellulare può seguire un percorso curvilineo, potendo essere chiuso o aperto. In questi casi, il tracciamento della posizione richiede due o tre coordinate. Questi sono rispettivamente movimenti nell'aereo e nello spazio. Questo ha a che fare con collegamenti: condizioni materiali che limitano il movimento. Alcuni esempi sono:
- Le orbite che descrivono i pianeti attorno al sole sono percorsi chiusi a forma di ellisse. Sebbene, in alcuni casi, possano essere approssimati a una circolare, come nel caso della Terra.
- La palla che il portiere calcia in un rinvio segue una traiettoria parabolica.
- Un uccello in volo descrive traiettorie curvilinee nello spazio, perché oltre a muoversi su un aereo può salire o scendere di livello a piacimento.
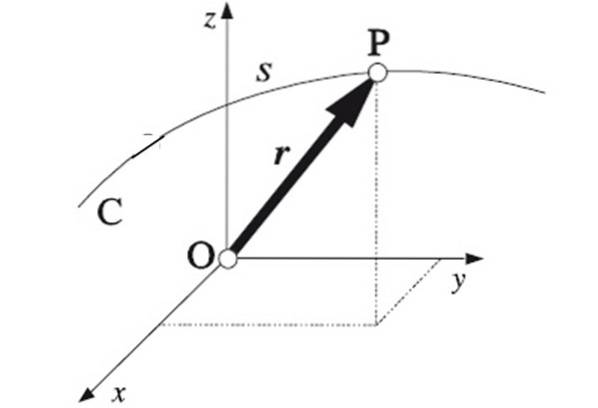
La traiettoria in fisica può essere espressa matematicamente quando la posizione del cellulare è nota in qualsiasi istante di tempo. Essere r il vettore di posizione, che a sua volta ha coordinate X, Y Y z nel caso più generale di un movimento in tre dimensioni. Conoscere la funzione r (t) la traiettoria sarà completamente determinata.
Indice articolo
In termini generali, la traiettoria può essere una curva piuttosto complicata, soprattutto se vuoi esprimerla matematicamente. Per questo inizia con i modelli più semplici, dove i cellulari viaggiano in linea retta o su un piano, che può essere il pavimento o qualsiasi altro adatto:
Le traiettorie più studiate sono:
- Rettilineo, quando si viaggia su una linea retta orizzontale, verticale o inclinata. Una palla lanciata verticalmente verso l'alto segue questo percorso, o segue un oggetto che scivola giù per un pendio. Sono movimenti unidimensionali, una singola coordinata è sufficiente per determinare completamente la loro posizione..
- Parabolico, in cui il mobile descrive un arco di parabola. È frequente, poiché qualsiasi oggetto lanciato obliquamente sotto l'azione della gravità (un proiettile) segue questa traiettoria. Per specificare la posizione del cellulare devi fornire due coordinate: X Y Y.
- Circolare, si verifica quando la particella in movimento segue un cerchio. È anche comune in natura e nella pratica quotidiana. Molti oggetti di uso quotidiano seguono un percorso circolare come pneumatici, parti di macchinari e satelliti in orbita, solo per citarne alcuni..
- Ellittica, l'oggetto si sposta seguendo un'ellisse. Come detto all'inizio, è il percorso seguito dai pianeti in orbita attorno al sole.
- Iperbolico, Gli oggetti astronomici sotto l'azione di una forza centrale (gravità), possono seguire traiettorie ellittiche (chiuse) o iperboliche (aperte), essendo queste meno frequenti delle prime.
- Elicoidale, o movimento a spirale, come quello di un uccello che ascende in una corrente termica.
- Altalena o pendolo, il cellulare descrive un arco nei movimenti avanti e indietro.
Le traiettorie descritte nella sezione precedente sono molto utili per avere un'idea veloce di come si muove un oggetto. In ogni caso, è necessario chiarire che la traiettoria di un cellulare dipende dalla posizione dell'osservatore. Ciò significa che lo stesso evento può essere visto in modi diversi, a seconda di dove si trova ogni persona..
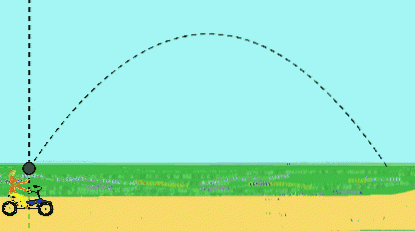
Ad esempio, una ragazza pedala a velocità costante e lancia una palla verso l'alto. Osserva che la palla descrive un percorso rettilineo.
Tuttavia, per un osservatore in piedi sulla strada che lo vede passare, la palla avrà un movimento parabolico. Per lui, la palla è stata inizialmente lanciata con una velocità inclinata, risultato della velocità verso l'alto dalla mano della ragazza più la velocità della bicicletta..
- Esplicito, specificando direttamente la curva o il luogo dato dall'equazione y (x)
- Implicito, in cui una curva è espressa come f (x, y, z) = 0
-Parametrico, in questa forma le coordinate x, yez sono date in funzione di un parametro generalmente scelto come tempo t. In questo caso, la traiettoria è composta dalle funzioni: x (t), e T) Y z (t).
Successivamente, vengono descritte due traiettorie ampiamente studiate in cinematica: la traiettoria parabolica e la traiettoria circolare..
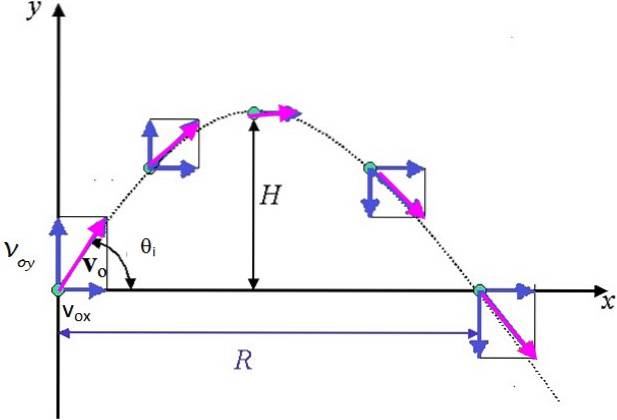
Un oggetto (il proiettile) viene lanciato con un angolo a con l'orizzontale e con la velocità iniziale vo come mostra l'immagine. La resistenza dell'aria non viene presa in considerazione. Il movimento può essere trattato come due movimenti indipendenti e simultanei: uno orizzontale a velocità costante e l'altro verticale sotto l'azione della gravità..
x (t) = xo +vbue.t
y (t) = yo +vHey.t -½g.tDue
Queste equazioni sono equazioni parametriche lancio di proiettili. Come spiegato sopra, hanno il parametro t, che ora è.
Quanto segue può essere visto nel triangolo rettangolo nella figura:
vbue = vo cos θio
vHey = vo sen θio
Sostituendo queste equazioni contenenti l'angolo di lancio nei risultati delle equazioni parametriche:
x (t) = xo +vo cos θio.t
y (t) = yo +vo. sen θio.t -½g.tDue
L'equazione esplicita del cammino si trova risolvendo t dall'equazione per x (t) e sostituendo nell'equazione y (t). Per facilitare il lavoro algebrico, si può presumere che l'origine (0,0) si trovi nel punto di lancio e quindi xo = eo = 0.
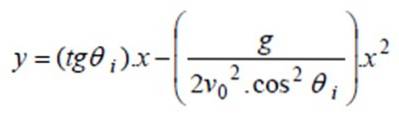
Questa è l'equazione del percorso in modo esplicito.
Un percorso circolare è dato da:
(x - xo)Due + (e eo)Due = RDue
Qui xo e eo rappresentano il centro del cerchio descritto dal mobile e R è il suo raggio. P (x, y) è un punto sul percorso. Dal triangolo rettangolo ombreggiato (figura 3) si può vedere che:
x = R. cos θ
y = R. sin θ
Il parametro, in questo caso, è l'angolo di sweep θ, chiamato spostamento angolare. Nel caso particolare che la velocità angolare ω (angolo spazzato per unità di tempo) sia costante, si può affermare che:
θ = θo + ωt
Dove θo è la posizione angolare iniziale della particella, che se presa come 0, si riduce a:
θ = ωt
In tal caso, il tempo ritorna alle equazioni parametriche come:
x = R.cos ωt
y = R. sin ωt
I vettori unitari io Y j sono molto convenienti per scrivere la funzione di posizione di un oggetto r (t). Indicano le direzioni sull'asse X e sull'asse Y rispettivamente. Nei suoi termini, la posizione di una particella che descrive un moto circolare uniforme è:
r (t) = R.cos ωt io + R. sen ωt j
Un cannone può sparare un proiettile con una velocità di 200 m / se un angolo di 40 ° rispetto all'orizzontale. Se il lancio è su terreno pianeggiante e la resistenza dell'aria è trascurata, trova:
a) L'equazione del percorso y (x) ...
b) Equazioni parametriche x (t) Y e T).
c) La distanza orizzontale e il tempo di permanenza del proiettile nell'aria.
d) L'altezza alla quale si trova il proiettile quando x = 12.000 m
a) Per trovare la traiettoria si sostituiscono i valori dati nell'equazione y (x) della sezione precedente:
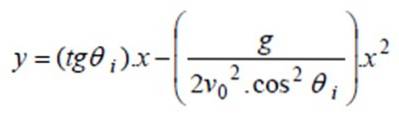
y (x) = tg 40º. X - 9.8 / (2 '400Due. cosDue40 °) XDue ⇒ y (x) = 0,8391 x - 0,0000522xDue
b) Il punto di lancio è scelto all'origine del sistema di coordinate (0,0):
x (t) = xo +vbue.t = 400'cos 40º.t = 306,42. t.
y (t) = yo +vHey.t -½g.tDue= 400 'sin 40º.t - 0,5 «9.8'tDue= 257,12 t - 4,9 tDue
c) Per trovare il tempo che il proiettile dura in aria, fallo y (t) = 0, essendo il varo effettuato su terreno pianeggiante:
0 = 257,12 t - 4,9 tDue
t = 257,12 / 4,9 s = 52,473 s
La portata orizzontale massima si trova sostituendo questo valore in x (t):
Xmax = 306,42'52 0,47 m = 16077,7 m
Un altro modo per trovare xmax direttamente è rendendo y = 0 nell'equazione del percorso:
0 = 0,8391 xmax - 0.0000522 xDuemax
x = 0,8391 / 0,0000522 m = 16078,5 m
C'è una piccola differenza dovuta all'arrotondamento dei decimali.
d) Per trovare l'altezza quando x = 12000 m, questo valore viene sostituito direttamente nell'equazione del percorso:
e (12000) = 0,8391«12000 - 0,0000522«12000Due m = 2552,4 m
La funzione di posizione di un oggetto è data da:
r (t) = 3t io + (4-5tDue) j m
Trova:
a) L'equazione per il percorso. Cos'è la curva?
b) La posizione iniziale e la posizione quando t = 2 s.
c) Lo spostamento effettuato dopo t = 2 s.
a) La funzione di posizione è stata data in termini di vettori unitari io Y j, che determinano rispettivamente la direzione sugli assi X Y Y, Quindi:
x (t) = 3t
e T) = 4 -5tDue
L'equazione del percorso y (x) si sta schiarendo t a partire dal x (t) e sostituendo y (t):
t = x / 3
y (x) = 4-5. (x / 3)Due = 4 - 5xDue/ 9 (Parabola)
b) La posizione di partenza è: r (2) = 4 j m ; la posizione in t = 2 s è r (2) = 6 io -16 j m
c) Spostamento Dr è la sottrazione dei due vettori di posizione:
Δr = r (Due) - r (2) = 6 io -16 j- 4 j = 6 io - venti j m
La Terra ha un raggio R = 6300 km ed è noto che il periodo di rotazione del suo movimento attorno al proprio asse è di un giorno. Trova:
a) L'equazione della traiettoria di un punto sulla superficie terrestre e la sua funzione di posizione.
b) La velocità e l'accelerazione di quel punto.
a) La funzione di posizione per qualsiasi punto in orbita circolare è:
r (t) = R.cos ωt io + R.sen ωt j
Abbiamo il raggio della Terra R, ma non la velocità angolare ω, tuttavia si può calcolare dal periodo, sapendo che per moto circolare vale dire che:
ω = 2π × frequenza = 2π / periodo
Il periodo del movimento è: 1 giorno = 24 ore = 1440 minuti = 86.400 secondi, quindi:
ω = 2π / 86400 s = 0,000023148 s-1
Sostituendo nella funzione di posizione:
r (t) = R.cos ωt io + R. sen ωt j = 6300 (cos 0.000023148t io + sen 0.000023148t j) Km
Il percorso in forma parametrica è:
x (t) = 6300. cos 0.000023148t
y (t) = 6300. sin 0,000023148t
b) Per il movimento circolare, l'ampiezza della velocità lineare v di un punto è correlato alla velocità angolare w attraverso:
v = ωR = 0,000023148 s-1'6300 Km = 0,1458 Km / s = 145,8 m / s
Pur essendo un movimento con velocità costante di 145,8 m / s, c'è un'accelerazione che punta verso il centro dell'orbita circolare, incaricata di mantenere il punto in rotazione. È l'accelerazione centripeta perc, dato da:
perc = vDue / R = (145,8 m / s)Due / 6300 × 103 m = 0,00337 m / sDue.
Nessun utente ha ancora commentato questo articolo.