Teorema fondamentale della dimostrazione aritmetica, applicazioni, esercizi

Il Il teorema fondamentale dell'aritmetica afferma che qualsiasi numero naturale maggiore di 1 può essere scomposto come prodotto di numeri primi - alcuni possono essere ripetuti - e questa forma è unica per quel numero, sebbene l'ordine dei fattori possa essere diverso.

Ricordalo un numero primo p È quello che ammette come divisori positivi solo se stesso e 1. I seguenti numeri sono primi: 2, 3, 5, 7, 11, 13 e così via, poiché ci sono infiniti. Il numero 1 non è considerato un primo, perché ha un unico divisore.

Da parte loro, vengono chiamati i numeri che non rispettano quanto sopra numeri composti, come 4, 6, 8, 9, 10, 12, 14 ... Prendiamo ad esempio il numero 10 e vediamo subito che può essere scomposto come prodotto di 2 e 5:

10 = 2 × 5

Sia 2 che 5 sono, effettivamente, numeri primi. Il teorema afferma che questo è possibile per qualsiasi numero n:

Dove p₁, p_Due, p₃... p_r sono numeri primi e k₁, K_Due, K₃,... K_r sono numeri naturali. Quindi i numeri primi agiscono come i mattoni da cui, attraverso la moltiplicazione, vengono costruiti i numeri naturali.

Indice articolo

• 1 Dimostrazione del teorema fondamentale dell'aritmetica
  • 1.1 Unicità della scomposizione in fattori primi
• 2 Applicazioni
  • 2.1 Numeri primi in natura
  • 2.2 Numeri primi e acquisti online
• 3 esercizi risolti
  • 3.1 - Esercizio 1
  • 3.2 - Esercizio 2
• 4 Riferimenti

Dimostrazione del teorema fondamentale dell'aritmetica

Iniziamo mostrando che ogni numero può essere scomposto in fattori primi. Sia un numero naturale n> 1, primo o composto.

Ad esempio, se n = 2, può essere espresso come: 2 = 1 × 2, che è primo. Allo stesso modo, procedi con i seguenti numeri:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Continuiamo così, scomponendo tutti i numeri naturali fino a raggiungere il numero n -1. Vediamo se riusciamo a farlo con il seguente numero: n.

Se n è primo, possiamo scomporlo come n = 1 × n, ma supponiamo che n sia composto e abbia un divisore d, logicamente minore di n:

1< d < n.

Se n / d = p₁, con P₁ un numero primo, quindi n viene scritto come:

n = p₁.d

Se d è primo non c'è più niente da fare, ma se non lo è c'è un numero n_Due che è un divisore di de minore di questo: n_Due < d, por lo que d podrá escribirse como el producto de n_Due da un altro numero primo p_Due:

d = p_Due n_Due

Che quando si sostituisce nel numero originale n darebbe:

n = p₁ .p_Due .n_Due

Supponiamo ora che n_Due o è un numero primo e lo scriviamo come il prodotto di un numero primo p₃, da un vostro divisore n₃, tale che n₃ < n_Due < n₁ < n:

n_Due = p₃.n₃ → n = p₁ p_Due p₃.n₃

 Ripetiamo questa procedura un numero finito di volte fino ad ottenere:

n = p₁.p_Due.p₃ ... p_r

Ciò significa che è possibile decomporsi tutti numeri interi da 2 a n, come prodotto di numeri primi.

Unicità della scomposizione in fattori primi

Verifichiamo ora che, ad eccezione dell'ordine dei fattori, questa scomposizione è unica. Supponiamo che n possa essere scritto in due modi:

n = p₁.p_Due.p₃ ... p_r = q_1.che cosa_Due.che cosa₃... che cosa_S  (con r ≤ s)

Ovviamente quello₁, che cosa_Due, che cosa₃... sono anche numeri primi. Come p₁ dividere a (q_1.che cosa_Due.che cosa₃... che cosa_S) Allora p₁ è uguale a una qualsiasi delle "q", non importa a cui, quindi possiamo dire che p₁ = q₁. Dividiamo n per p₁ e otteniamo:

p_Due.p₃ ... p_r =_.che cosa_Due.che cosa₃... che cosa_S

Ripetiamo la procedura finché non dividiamo tutto per p_r, quindi otteniamo:

1 = q_{r + 1}... che cosa_S

Ma non è possibile arrivare a cosa_{r + 1}... che cosa_S = 1 quando r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Applicazioni

Come abbiamo detto prima, i numeri primi rappresentano, se vuoi, gli atomi dei numeri, le loro componenti di base. Quindi il teorema fondamentale dell'aritmetica ha numerose applicazioni, la più ovvia: possiamo lavorare più facilmente con numeri grandi se li esprimiamo come il prodotto di numeri più piccoli..

Allo stesso modo, possiamo trovare il massimo comune multiplo (LCM) e il massimo comune divisore (GCF), una procedura che ci aiuta a fare più facilmente somme di frazioni, trovare radici di grandi numeri, o operare con radicali, razionalizzare e risolvere problemi applicativi di natura molto varia.

Inoltre, i numeri primi sono estremamente enigmatici. Uno schema non è ancora riconosciuto in loro e non è possibile sapere quale sarà il prossimo. Il più grande finora è stato trovato dai computer e ha 24.862.048 cifre, sebbene i nuovi numeri primi appaiano ogni volta meno frequentemente.

Numeri primi in natura

Le cicale, cicale o cicale che vivono nel nord-est degli Stati Uniti emergono in cicli di 13 o 17 anni. Sono entrambi numeri primi.

In questo modo le cicale evitano di coincidere con predatori o concorrenti che hanno altri periodi di nascita, né le diverse varietà di cicale competono tra loro, poiché non coincidono durante lo stesso anno..

Numeri primi e acquisti online

I numeri primi vengono utilizzati in crittografia per mantenere segreti i dettagli della carta di credito quando si effettuano acquisti su Internet. In questo modo i dati che l'acquirente arrivano proprio in negozio senza perdersi o cadere nelle mani di persone senza scrupoli..

Come? I dati sulle carte sono codificati in un numero N che può essere espresso come prodotto di numeri primi. Questi numeri primi sono la chiave che i dati rivelano, ma sono sconosciuti al pubblico, possono essere decodificati solo sul web a cui sono diretti.

Decomporre un numero in fattori è un compito facile se i numeri sono piccoli (vedi gli esercizi risolti), ma in questo caso si usano come chiave i numeri primi di 100 cifre, che moltiplicandoli danno numeri molto più grandi, la cui scomposizione dettagliata implica un compito enorme.

Esercizi risolti

- Esercizio 1

Scomponi 1029 in fattori primi.

Soluzione

1029 è divisibile per 3. È noto perché sommando le sue cifre la somma è un multiplo di 3: 1 + 0 + 2 + 9 = 12. Poiché l'ordine dei fattori non altera il prodotto, possiamo iniziare da lì:

1029 3

343

1029 = 3 × 343

D'altra parte 343 = 7³, poi:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

E poiché sia ​​3 che 7 sono numeri primi, questa è la scomposizione di 1029.

- Esercizio 2

Fattorizzare il trinomio x^Due + 42x + 432.

Soluzione

Il trinomio viene riscritto nella forma (x + a). (x + b) e dobbiamo trovare i valori di aeb, tali che:

a + b = 42; a.b = 432

Il numero 432 viene scomposto in fattori primi e da lì viene scelta la combinazione appropriata per tentativi ed errori in modo che i fattori aggiunti diano 42.

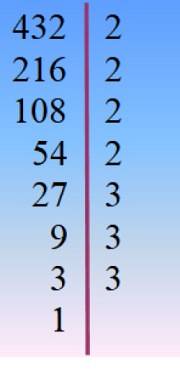
432 = 2⁴ × 3³ = 2 × 3³× 2³ = 2⁴× 3^Due × 3 = ...

Da qui ci sono diverse possibilità per scrivere 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72 ... .

E tutti possono essere trovati combinando prodotti tra i fattori primi, ma per risolvere l'esercizio proposto, l'unica combinazione adatta è: 432 = 24 × 18 poiché 24 + 18 = 42, quindi:

X^Due + 42x + 432 = (x + 24). (x +18)

Riferimenti

1. Baldor, A. 1986. Aritmetica pratica teorica. Compañía Cultural Editora de Textos Americanos S.A.
2. BBC World. Il codice della natura nascosto. Estratto da: bbc.com.
3. De Leon, Manuel Prime numbers: i guardiani di Internet. Estratto da: blogs.20minutos.es.
4. UNAM. Teoria dei numeri I: Teorema fondamentale dell'aritmetica. Estratto da: teoriadenumeros.wikidot.com.
5. Wikipedia. Il teorema fondamentale dell'aritmetica. Estratto da: es.wikipedia.org.