
Teorema del fattore di spiegazione, esempi, esercizi
Il teorema dei fattori afferma che un polinomio P (x) è divisibile per un binomio della forma (x - a) se x = a è una radice di P (x), cioè P (a) = 0. Si dice che un polinomio è divisibile tra un altro quando il suo residuo o resto è zero.
Un polinomio è un'espressione della forma:
P (x) = an Xn + pern-1 Xn-1 +... + A1 x + a0

Dove:
-n è il grado del polinomio, dove n è il numero intero più grande a cui viene elevata la variabile indipendente x,
-I valori an, pern-1 ,... + A1 , per0 sono i coefficienti del polinomio, che sono generalmente numeri reali, ma potrebbero anche essere numeri complessi.
Un polinomio di grado n può essere scomposto come prodotto di n binomi della forma:
(x - rio)
Dove rio è l'i-esima radice di P (x):
P (x) = an (x - r1) (x - rDue) ... (X - rn)
Poiché il numero di radici di un polinomio è uguale al suo grado.
Indice articolo
- 1 Esempi
- 1.1 - Esempio 1
- 1.2 - Esempio 2
- 2 esercizi
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Esempi
- Esempio 1
Consideriamo per caso il polinomio:
P (x) = 3⋅xDue - 7⋅x + 2
Vuoi sapere se questo polinomio è divisibile per il binomio (x - 2). Se viene utilizzato il teorema dei fattori, dobbiamo valutare P (x = 2) per sapere se il valore 2 è una radice o non lo è. Si procede quindi a valutare l'espressione:
P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12-14 + 2 = 12-12 = 0.
Risulta che x = 2 è la radice di P (x), quindi secondo il teorema dei fattori, il binomio (x - 2) è effettivamente un fattore di P (x).
Passiamo alla verifica diretta dividendo. Il dettaglio di come viene eseguita la divisione è mostrato nella figura seguente:
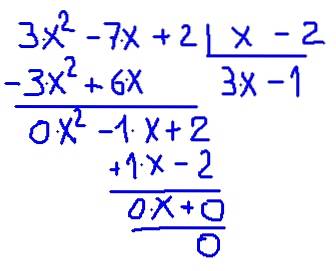
Si verifica che il quoziente tra P (x) e (x-2) dà un polinomio di grado inferiore detto quoziente C (x) = 3⋅x - 1 con resto 0.
Possiamo riassumere il risultato come segue:
(3⋅xDue - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0
L'espressione precedente può essere scritta in un altro modo, ricordando semplicemente che il dividendo P (x) è uguale al prodotto del divisore (x -2) per il quoziente (3⋅x - 1) più il resto (zero in questo caso ):
(3⋅xDue - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0
In questo modo è stato possibile fattorizzare il polinomio P (x), ovvero scrivere come prodotto di polinomi, il polinomio originale:
(3⋅xDue - 7⋅x + 2) = (x -2) (3⋅x - 1)
- Esempio 2
Sia il polinomio Q (x) = x3 - x + 2. Vogliamo sapere se è divisibile per il binomio (x + 1).
Il modo più diretto è semplicemente applicare il teorema dei fattori. In questo caso dobbiamo semplicemente verificare se x = -1 annulla o meno il polinomio Q (x).
Si procede sostituendo:
Q (-1) = (-1)3 - (-1) + 2 = -1 + 1 + 2 = 2
Il risultato è diverso da zero, quindi il teorema dei fattori ci assicura che il polinomio Q (x) non è divisibile per (x + 1), poiché Q (-1) ≠ 0.
Ora procederemo ad effettuare la divisione di Q (x) per il binomio (x + 1) come metodo di verifica della nostra conclusione.
In questa occasione, la divisione verrà effettuata utilizzando il metodo della divisione sintetica, che consiste nel porre in prima riga ordinati dal grado più alto a zero gradi tutti i coefficienti del polinomio, compresi quelli mancanti, poiché hanno coefficiente zero.
Quindi nella prima colonna viene posto il termine indipendente del divisore ma con il segno cambiato, nel nostro caso il divisore è (x + 1). Il suo termine indipendente è 1, ma come nella prima colonna è posto cambiato segno, cioè -1.
La figura seguente mostra come viene eseguita la divisione sintetica:

Con questo risultato si verifica che (x + 1) non è un fattore del polinomio Q (x) = x3 - x + 2 poiché il resto è diverso da zero.
Questa conclusione non è sorprendente, perché era già stata prevista con il teorema dei fattori. Si noti inoltre che quando si sostituisce x = -1 in Q (x) ciò che si ottiene è precisamente il resto o il resto della divisione dei polinomi, poiché Q (-1) = resto = 2.
Naturalmente, la divisione fornisce le informazioni aggiuntive del quoziente C (x) = xDue - X.
Ricordando che il dividendo Q (x) è uguale al divisore (x + 1) per il quoziente C (x) più il resto r = 2, abbiamo l'espansione del polinomio Q (x) come segue:
Q (x) = (x + 1) (xDue - x) + 2 = x (x + 1) (x - 1) + 2
Va notato che questa espressione non è la fattorizzazione di detto polinomio, poiché c'è un termine diverso da zero che si somma, che è precisamente il resto del valore 2.
Formazione
- Esercizio 1
Trova i fattori del polinomio
P (x) = x3 - 5 xDue + 2 x + 8
E scrivi anche la tua fattorizzazione.
Soluzione
Il teorema dei fattori ci dice che dobbiamo cercare le radici per per poi trovare i fattori (x - per), in questo caso trattandosi di un polinomio di grado tre, devono esserci tre radici.
Trattandosi di un polinomio a coefficienti interi, le radici devono trovarsi tra i divisori del termine indipendente, che in questo caso è 8. Questi divisori sono:
± 1, ± 2, ± 4, ± 8.
Iniziamo esplorando +1: P (+1) = 13 - 5⋅ 1Due + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6 che è diverso da 0, quindi +1 non è una radice.
Esploriamo -1:
P (-1) = (-1)3 - 5⋅ (-1)Due + 2⋅ (-1) + 8 = -1-5-2 + 8 = 0
Dal risultato si conclude che -1 è la radice di P (x) e (x - (-1)) = (x + 1) è un fattore del polinomio.
Restano da trovare altri due fattori:
Dimostriamo quanto segue che è +2:
P (+2) = (+2)3 - 5⋅ (+2)Due + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0
Ancora una volta otteniamo zero. Quindi l'altro fattore è (x - 2).
Poiché è un polinomio di grado tre, dobbiamo solo trovare un fattore. Ora testiamo il valore +4 per scoprire se annulla il polinomio:
P (+4) = (+4)3 - 5⋅ (+4)Due + 2⋅ (+4) + 8 = 64-80 + 8 + 8 = 0.
Cioè, +4 è la radice di P (x) e quindi il binomio (x - 4) è un altro dei suoi fattori.
Niente più ricerche, perché è un polinomio di grado 3 che ha al massimo tre radici. In questo esercizio tutte le radici si sono rivelate reali e intere.
Pertanto il polinomio P (x) viene scomposto in questo modo:
P (x) = x3 - 5 xDue + 2 x + 8 = (x + 1) (x - 2) (x - 4).
- Esercizio 2
Sia p⋅x il polinomio3 - x + 2p. Determina il valore di p in modo che il polinomio sia divisibile per (x + 2).
Soluzione
Usiamo il teorema del fattore, che afferma che se x = -2 annulla il polinomio allora (x - (-2)) è un fattore di detto polinomio.
Quindi sostituiamo x per (-2) nel polinomio originale, lo semplifichiamo e lo poniamo uguale a zero:
p⋅ (-2)3 - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0
Ora il valore di p viene cancellato in modo che l'uguaglianza a zero sia soddisfatta:
p = -2 / 10 = -⅕
Ciò significa che il polinomio:
-⅕⋅x3 - x - ⅖
È divisibile per (x + 2) o per ciò che è equivalente: (x + 2) è uno dei suoi fattori.
Riferimenti
- Baldor Aurelio. Algebra. Grupo Editorial Patria.
- Demana, W. Precalculus: Grafico, Numerico, Algebrico 7 ° Ed. Pearson Education.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5 °. Edizione. Cengage Learning.
- Zill, D. 1984. Algebra e trigonometria. Mcgraw hill.


Nessun utente ha ancora commentato questo articolo.