
Spiegazione, applicazioni, esercizi del teorema di Bayes
Il Teorema di Bayes è una procedura che ci permette di esprimere la probabilità condizionata di un evento casuale A dato B, in termini di distribuzione di probabilità dell'evento B dato A e distribuzione di probabilità solo A.
Questo teorema è molto utile, poiché grazie ad esso possiamo mettere in relazione la probabilità che si verifichi un evento A sapendo che si è verificato B, con la probabilità che si verifichi il contrario, cioè che B si verifichi dato A.
Il teorema di Bayes era una proposizione d'argento del reverendo Thomas Bayes, un teologo inglese del XVIII secolo che era anche un matematico. Fu autore di numerose opere di teologia, ma attualmente è noto per un paio di trattati di matematica, tra i quali spicca come principale risultato il già citato Teorema di Bayes.
Bayes ha affrontato questo teorema in un lavoro intitolato "An Essay Verso la risoluzione di un problema nella Dottrina delle Possibilità", pubblicato nel 1763, e sul quale sono stati sviluppati molti studi con applicazioni in varie aree della conoscenza.
Indice articolo
- 1 Spiegazione
- 2 Applicazioni del teorema di Bayes
- 2.1 Esercizi risolti
- 3 Riferimenti
Spiegazione
Innanzitutto, per una migliore comprensione di questo teorema, sono necessarie alcune nozioni di base della teoria della probabilità, in particolare il teorema della moltiplicazione per la probabilità condizionata, che afferma che
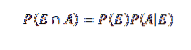
Per E e A eventi arbitrari di uno spazio campionario S.
E la definizione di partizioni, che ci dice che se abbiamo A1 ,PERDue,… , PERn eventi di uno spazio campionario S, questi formeranno una partizione di S, se Aio si escludono a vicenda e la loro unione è S.
Detto questo, sia B un altro evento. Quindi possiamo vedere B come
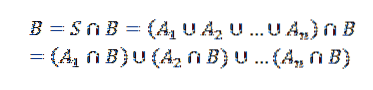
Dove l'Aio intersecati con B sono eventi che si escludono a vicenda.
E di conseguenza,
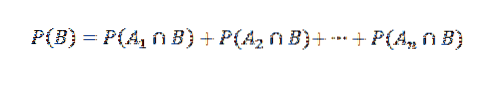
Quindi, applicando il teorema della moltiplicazione
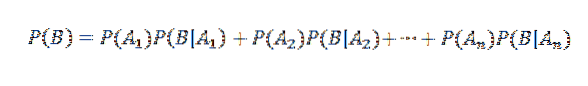
D'altra parte, la probabilità condizionata di Ai dato B è definita da
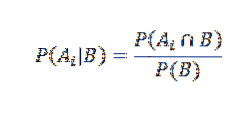
Sostituendo in modo appropriato abbiamo quello per qualsiasi i
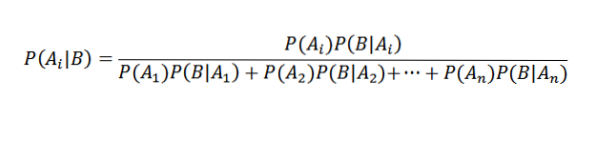
Applicazioni del teorema di Bayes
Grazie a questo risultato, gruppi di ricerca e varie società sono riusciti a migliorare i sistemi che si basano sulla conoscenza..
Ad esempio, nello studio delle malattie, il teorema di Bayes può aiutare a discernere la probabilità che una malattia si trovi in un gruppo di persone con una data caratteristica, prendendo come dati i tassi globali della malattia e la predominanza di dette caratteristiche in entrambi persone sane e malate.
D'altra parte, nel mondo delle alte tecnologie, ha influenzato grandi aziende che hanno sviluppato, grazie a questo risultato, software "Knowledge-Based".
Come esempio quotidiano abbiamo l'assistente di Microsoft Office. Il teorema di Bayes aiuta il software a valutare i problemi che l'utente presenta e determinare quale consiglio fornire e quindi essere in grado di offrire un servizio migliore in base alle abitudini dell'utente.
Va notato che questa formula è stata ignorata fino a tempi recenti, principalmente perché quando questo risultato è stato sviluppato 200 anni fa, c'era poco uso pratico per loro. Tuttavia, ai nostri giorni, grazie a grandi progressi tecnologici, gli scienziati hanno trovato il modo per mettere in pratica questo risultato.
Esercizi risolti
Esercizio 1
Una compagnia di telefoni cellulari ha due macchine A e B. Il 54% dei telefoni cellulari prodotti sono realizzati dalla macchina A e il resto dalla macchina B. Non tutti i telefoni cellulari prodotti sono in buone condizioni.
La proporzione di telefoni cellulari difettosi prodotti da A è 0,2 e da B è 0,5. Qual è la probabilità che un telefono cellulare di quella fabbrica sia difettoso? Qual è la probabilità che, sapendo che un telefono cellulare è difettoso, provenga dalla macchina A?
Soluzione
Qui hai un esperimento che viene eseguito in due parti; nella prima parte si verificano gli eventi:
A: cella realizzata dalla macchina A.
B: cella realizzata dalla macchina B.
Poiché la macchina A produce il 54% dei telefoni cellulari e il resto è prodotto dalla macchina B, ne consegue che la macchina B produce il 46% dei telefoni cellulari. Vengono fornite le probabilità di questi eventi, ovvero:
P (A) = 0,54.
P (B) = 0,46.
Gli eventi della seconda parte dell'esperimento sono:
D: cellulare difettoso.
E: cellulare non difettoso.
Come affermato nella dichiarazione, le probabilità di questi eventi dipendono dal risultato ottenuto nella prima parte:
P (D | A) = 0,2.
P (D | B) = 0,5.
Utilizzando questi valori si possono determinare anche le probabilità dei complementi di questi eventi, ovvero:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Y
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Ora l'evento D può essere scritto come segue:
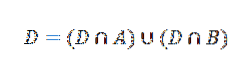
Utilizzo del teorema di moltiplicazione per i risultati di probabilità condizionata:
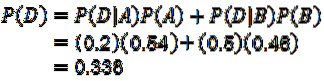
Con cui si risponde alla prima domanda.
Ora dobbiamo solo calcolare P (A | D), per il quale viene applicato il teorema di Bayes:
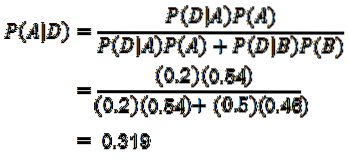
Grazie al Teorema di Bayes, si può affermare che la probabilità che un cellulare sia stato fabbricato dalla macchina A, sapendo che il cellulare è difettoso, è 0,319.
Esercizio 2
Tre scatole contengono palline bianche e nere. La composizione di ciascuno di essi è la seguente: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
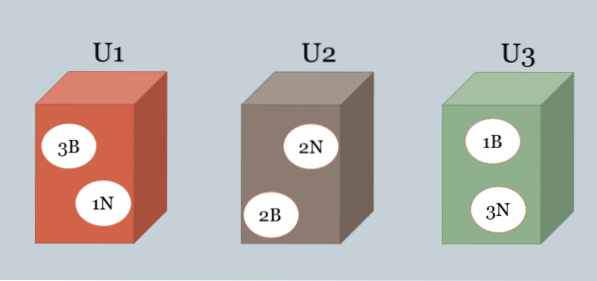
Una delle caselle viene scelta a caso e viene estratta una pallina che risulta essere bianca. Qual è la scatola che più probabilmente è stata scelta?
Soluzione
Utilizzando U1, U2 e U3, rappresenteremo anche la casella scelta.
Questi eventi costituiscono una partizione di S e si verifica che P (U1) = P (U2) = P (U3) = 1/3 poiché la scelta della scatola è casuale.
Se B = la palla estratta è bianca, avremo P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Quello che vogliamo ottenere è la probabilità che la pallina sia stata tolta dalla scatola Ui sapendo che la pallina era bianca, ovvero P (Ui | B), e vedere quale dei tre valori era il più alto da conoscere di cui scatola è stata molto probabilmente l'estrazione della pallina bianca.
Applicando il teorema di Bayes al primo dei riquadri:
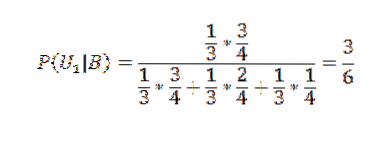
E per gli altri due:
P (U2 | B) = 2/6 e P (U3 | B) = 1/6.
Quindi, la prima delle caselle è quella con la più alta probabilità di essere stata scelta per l'estrazione della pallina bianca..
Riferimenti
- Kai Lai Chung. Teoria elementare della proabilità con processi stocastici. Springer-Verlag New York Inc
- Kenneth.H. Rosen Matematica discreta e sue applicazioni. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Probabilità e applicazioni statistiche. S.A. MESSICANO ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Problemi risolti di matematica discreta. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teoria e problemi di probabilità. McGRAW-HILL.

Nessun utente ha ancora commentato questo articolo.