
Somma telescopica come si risolve e si risolvono gli esercizi

Il somma telescopico è un ramo delle operazioni con serie di numeri. Affronta la somma di elementi da un valore iniziale a "n" di espressioni il cui argomento obbedisce a uno dei seguenti modelli:
(FX - Fx + 1); (Fx + 1 - FX)
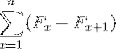
Come pure:
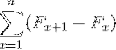

Rappresentano una sommatoria di elementi che, una volta sviluppati, è soggetta ad annullamenti di termini opposti. Consentendo di definire la seguente uguaglianza per le sommatorie telescopiche:
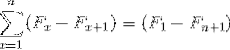
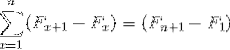
Il suo nome deriva dal rapporto con l'aspetto di un telescopio classico, che poteva essere piegato e aperto, cambiando notevolmente la sua dimensione. Allo stesso modo, le sommatorie telescopiche, di natura infinita, possono essere riassunte nell'espressione semplificata:
F1 - Fn + 1
Indice articolo
- 1 demo
- 2 Come risolvere?
- 2.1 Decomposizione in frazioni semplici
- 3 Storia
- 4 esercizi
- 4.1 Esercizio 1
- 4.2 Esercizio 2
- 5 Riferimenti
Dimostrazione
Quando si sviluppa la somma dei termini, l'eliminazione dei fattori è abbastanza ovvia. Dove per ciascuno dei casi, nella successiva iterazione appariranno elementi opposti.
Il primo caso, (FX - Fx + 1), poiché il processo funziona in modo omologato per (Fx + 1-FX).
Sviluppando i primi 3 valori 1, 2, 3 si osserva la tendenza alla semplificazione
X1 (F1 - F1 + 1) = F1 - FDue
XDue (FDue - F2 + 1) = FDue - F3
X3 (F3 - F3 + 1) = F3 - F4
Dove quando si esprime la somma degli elementi descritti:
X1 + XDue + X3 = F1 - FDue + FDue - F3 + F3 - F4
Si osserva che i termini FDue e F3 sono descritti insieme ai loro opposti, il che rende inevitabile la loro semplificazione. Allo stesso modo, si osserva che i termini F1 e F4 rimanere.
Se la somma è stata fatta da x = 1 ax = 3, significa che l'elemento F4 corrisponde al termine generico Fn + 1.
Dimostrando così l'uguaglianza:
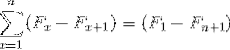
Come si risolve?
Lo scopo delle sommatorie telescopiche è di facilitare il lavoro, in modo che non sia necessario sviluppare un numero infinito di termini, o di semplificare qualche catena di addendi troppo lunga.
Per la sua risoluzione sarà solo necessario valutare i termini F.1 e Fn + 1. Queste semplici sostituzioni costituiscono il risultato finale della somma.
La totalità dei termini non verrà espressa, rendendosi necessaria solo per la dimostrazione del risultato, ma non per il normale processo di calcolo.
L'importante è notare la convergenza delle serie numeriche. A volte l'argomento della sommatoria non verrà espresso in modo telescopico. In questi casi, l'implementazione di metodi di factoring alternativi è molto comune..
Il metodo di fattorizzazione caratteristico nelle addizioni telescopiche è quello delle frazioni semplici. Ciò si verifica quando una frazione originale viene scomposta in una somma di più frazioni, dove il modello telescopico (FX - Fx + 1) o (Fx + 1 - FX).
Decomposizione in frazioni semplici
Per verificare la convergenza delle serie numeriche, è molto comune trasformare espressioni razionali con il metodo delle frazioni semplici. L'obiettivo è modellare la trama nella forma di una sommatoria telescopica..
Ad esempio, la seguente uguaglianza rappresenta una scomposizione in semplici frazioni:
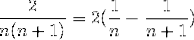
Quando si sviluppa la serie numerica e si applicano le proprietà corrispondenti, l'espressione assume la forma seguente:
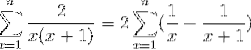
Dove la forma telescopica (FX - Fx + 1).
La procedura è abbastanza intuitiva e consiste nel trovare i valori del numeratore che, senza rompere l'uguaglianza, permettono di separare i prodotti che si trovano al denominatore. Le equazioni che sorgono nella determinazione di questi valori, vengono sollevate in base a confronti tra entrambi i lati dell'uguaglianza.
Questa procedura viene osservata passo dopo passo nello sviluppo dell'esercizio 2.
Storia
È abbastanza incerto poter definire il momento storico in cui sono state presentate le somme telescopiche. Tuttavia, la sua attuazione inizia a essere vista nel XVII secolo, negli studi di serie numeriche condotti da Leibniz e Huygens..
Entrambi i matematici, esplorando le somme di numeri triangolari, iniziano a notare tendenze nella convergenza di alcune serie di elementi successivi. Ma ancora più interessante è l'inizio della modellazione di queste espressioni, in elementi che non necessariamente si susseguono.
Infatti, l'espressione usata in precedenza per riferirsi a frazioni semplici:
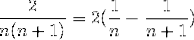
Fu introdotto da Huygens e catturò immediatamente l'attenzione di Leibniz. Chi nel tempo ha potuto osservare la convergenza al valore 2. Senza saperlo, ha implementato il formato della sommatoria telescopica.
Formazione
Esercizio 1
Definisci a quale termine converge la seguente somma:
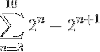
Quando si sviluppa manualmente la somma, si osserva il seguente schema:
(Due3 - Due4) + (24 - Due5) + (25 - Due6)… (Due10 - Dueundici)
Dove i fattori da 24 fino a 210 Presentano parti positive e negative, rendendo evidente la loro cancellazione. Quindi gli unici fattori che non verranno semplificati saranno i primi "23"E l'ultimo" 2undici".
In questo modo, implementando il criterio della sommatoria telescopica, si ottiene:
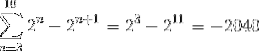
Esercizio 2
Trasforma l'argomento in una somma di tipo telescopico e definisci la convergenza delle serie:
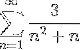
Come indicato nell'affermazione, la prima cosa da fare sarà scomporre in semplici frazioni, in modo da riaffermare l'argomento ed esprimerlo in modo telescopico..
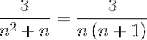
Devi trovare 2 frazioni i cui denominatori siano rispettivamente "n" e "n + 1", dove il metodo utilizzato di seguito deve ottenere i valori del numeratore che soddisfano l'uguaglianza.
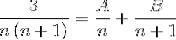
Procediamo per definire i valori di A e B. Innanzitutto, sommiamo le frazioni.
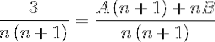
Quindi, i denominatori vengono semplificati e viene stabilita un'equazione lineare.
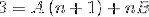
Nella fase successiva, viene utilizzata l'espressione a destra, fino a ottenere un modello paragonabile al "3" a sinistra..
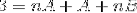
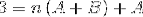
Per definire le equazioni da utilizzare, è necessario confrontare i risultati di entrambi i lati dell'uguaglianza. Ovvero non si osservano valori della variabile n sul lato sinistro, in questo modo A + B dovrà essere uguale a zero.
A + B = 0; A = -B
D'altra parte, il valore della costante A dovrà essere uguale al valore della costante 3.
A = 3
Perciò.
A = 3 e B = -3
Una volta definiti i valori del numeratore per le frazioni semplici, la somma viene riformulata.
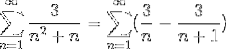
Dove la forma generica di sommatoria telescopica è già stata raggiunta. Viene sviluppata la serie telescopica.
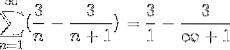
Dove dividendo per un numero molto grande il risultato si avvicinerà sempre di più a zero, osservando la convergenza della serie al valore 3.
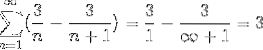
Questo tipo di serie non potrebbe essere risolto in altro modo, a causa del numero infinito di iterazioni che definiscono il problema. Tuttavia, questo metodo, insieme a molti altri, inquadra il ramo di studio delle serie numeriche, il cui obiettivo è determinare i valori di convergenza o definire la divergenza di dette serie..
Riferimenti
- Infinitesimali lezioni di calcolo. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. EDITUM, 1994.
- Calcolo integrale: successioni e serie di funzioni. Antonio Rivera Figueroa. Grupo Editorial Patria, 21 ottobre. 2014.
- Un corso di calcolo e analisi reale. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 giugno. 2006.
- Serie infinita. Tomlinson Fort. The Clarendon Press, 1930.
- Elementi della teoria dei processi infiniti. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorporated, 1923.


Nessun utente ha ancora commentato questo articolo.