
Riemann riassume la storia, le formule e le proprietà, gli esercizi
Il Somma di Riemann è il nome dato al calcolo approssimativo di un integrale definito, mediante una sommatoria discreta con un numero finito di termini. Un'applicazione comune è l'approssimazione dell'area delle funzioni su un grafico.
Fu il matematico tedesco Georg Friedrich Bernhard Riemann (1826-1866) a offrire per primo una definizione rigorosa dell'integrale di una funzione in un dato intervallo. Lo ha reso noto in un articolo pubblicato nel 1854.
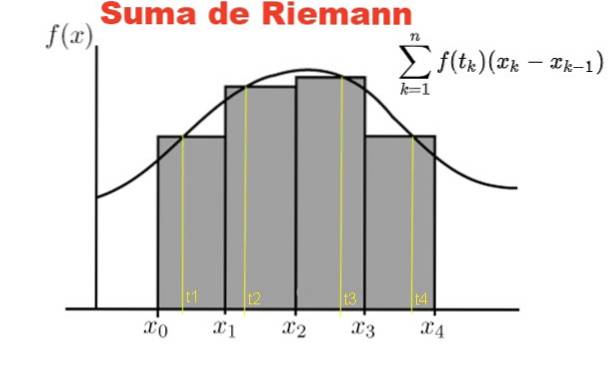
La somma di Riemann è definita su una funzione y = f (x), con x appartenente all'intervallo chiuso [a, b]. In questo intervallo viene realizzata una partizione P di n elementi:
P = x0= a, x1, XDue,..., Xn= b
Ciò significa che l'intervallo è suddiviso come segue:

Xk-1 ≤ tK ≤ xK
La Figura 1 mostra graficamente la somma di Riemann della funzione f sull'intervallo [x0, X4] su una partizione di quattro sottointervalli, i rettangoli grigi.
La somma rappresenta l'area totale dei rettangoli e il risultato di questa somma approssima numericamente l'area sotto la curva f, tra le ascisse x = x0 y x = x4.
Ovviamente, l'approssimazione all'area sotto la curva migliora notevolmente con il numero n partizioni è più grande. In questo modo la somma converge all'area sotto la curva, quando il numero n delle partizioni tende all'infinito.
Indice articolo
- 1 Formule e proprietà
- 1.1 L'area sotto la curva
- 2 Esercizi risolti
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Formule e proprietà
La somma di Riemann della funzione f (x) sulla partizione:
P = x0= a, x1, XDue,..., Xn= b
Definito sull'intervallo [a, b], è dato da:
S (P, f) = ∑k = 1n f (tK) (XK - Xk-1)
DoveK è un valore nell'intervallo [xK, Xk-1]. Nella somma di Riemann si usano solitamente intervalli regolari di larghezza Δx = (b - a) / n, dove aeb sono i valori minimo e massimo dell'ascissa, mentre n è il numero di suddivisioni.
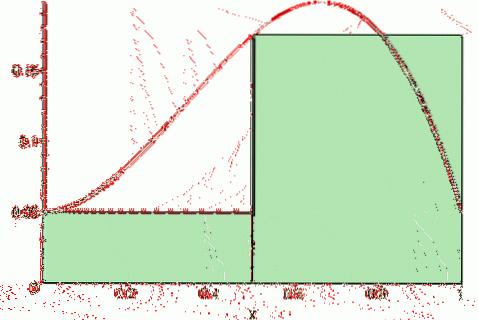
In tal caso, il file Riemann giusta somma è:
Sd (f, n) = [f (a + Δx) + f (a + 2Δx) +… + f (a + (n-1) Δx) + f (b)] * Δx
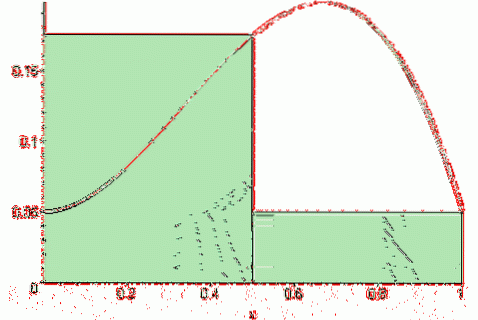
Mentre il Riemann ha lasciato la somma è espresso come:
Se (f, n) = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx
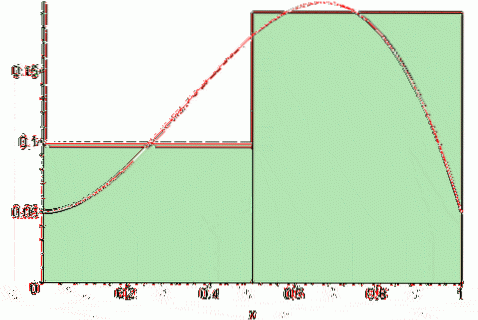
Infine il somma di Riemann centrale è:
Sc (f, n) = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx
A seconda di dove si trova il punto tK sull'intervallo [xK, Xk-1] la somma di Riemann può sovrastimare o sottostimare il valore esatto dell'area sotto la curva della funzione y = f (x). In altre parole, i rettangoli possono sporgere dalla curva o essere leggermente al di sotto di essa..
L'area sotto la curva
La proprietà principale della somma di Riemann e da cui deriva la sua importanza è che se il numero delle suddivisioni tende all'infinito, il risultato della somma converge all'integrale definito della funzione:

Esercizi risolti
- Esercizio 1
Calcola il valore dell'integrale definito tra a = -2 e b = +2 della funzione:
f (x) = xDue
Usa una somma di Riemann. Per fare ciò, trova prima la somma di n partizioni regolari dell'intervallo [a, b] e poi prendi il limite matematico per il caso in cui il numero di partizioni tende all'infinito.
Soluzione
Questi sono i passaggi da seguire:
-Per prima cosa, definisci l'intervallo delle partizioni come:
Δx = (b - a) / n.
-Quindi la somma di Riemann da destra corrispondente alla funzione f (x) ha questo aspetto:


[-2 + (4i / n)]Due = 4 - (16 i / n) + (4 / n)Due ioDue
-E poi viene accuratamente sostituito nella sommatoria:

-Il passaggio successivo consiste nel separare le somme e prendere le quantità costanti come fattore comune di ciascuna somma. Occorre tener conto che l'indice è i, quindi i numeri e i termini con n sono considerati costanti:

-Ogni sommatoria viene valutata, poiché per ciascuna di esse esistono espressioni appropriate. Ad esempio, la prima delle somme dà n:



S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6nDue
-Infine, abbiamo che l'integrale che vogliamo calcolare è:

= 16 - (64/2) + (64/3) = 16/3 = 5.333
Il lettore può verificare che questo è il risultato esatto, ottenibile risolvendo l'integrale indefinito e valutando i limiti di integrazione secondo la regola di Barrow.
- Esercizio 2
Determinare approssimativamente l'area sotto la funzione:
f (x) = (1 / √ (2π)) e(-XDue/Due)
Immettere x = -1 ex = + 1, utilizzando una somma di Riemann centrale con 10 partizioni. Confronta con il risultato esatto e stima la differenza percentuale.
Soluzione
Il passo o incremento tra due valori discreti successivi è:
Δx = (1 - (-1) / 10 = 0,2
Quindi la partizione P su cui sono definiti i rettangoli si presenta così:
P = -1,0; -0,8; -0.6; -0.4; -0,2; 0,0; 0.2; 0.4; 0.6; 0,8; 1.0
Ma poiché ciò che si vuole è la somma centrale, la funzione f (x) sarà valutata nei punti medi dei sottointervalli, cioè nell'insieme:
T = -0,9; -0,7; -0,5; -0.3; -0,1; 0,1; 0,3; 0,5; 0,7; 0.9.
La somma (centrale) di Riemann si presenta così:
S = f (-0,9) * 0,2 + f (-0,7) * 0,2 + f (-0,5) * 0,2 +… + f (0,7) * 0,2 + f (0,9) * 0,2
Poiché la funzione f è simmetrica, è possibile ridurre la somma a soli 5 termini e il risultato viene moltiplicato per due:
S = 2 * 0,2 * f (0,1) + f (0,3) + f (0,5) + f (0,7) + f (0,9)
S = 2 * 0,2 * 0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683
La funzione data in questo esempio non è altro che la ben nota campana gaussiana (normalizzata, con media uguale a zero e deviazione standard uno). L'area sotto la curva nell'intervallo [-1,1] per questa funzione è nota come 0.6827.

Ciò significa che la soluzione approssimativa con soli 10 termini corrisponde alla soluzione esatta con tre cifre decimali. L'errore percentuale tra l'integrale approssimativo e quello esatto è 0,07%.
Riferimenti
- Casteleiro, J. M. e Gómez-Álvarez, R. P. (2002). Calcolo integrale (Illustrato ed.). Madrid: editoriale ESIC.
- Unican. Storia del concetto di integrale. Estratto da: repositorio.unican.es
- UIS. Riemann riassume. Estratto da: matematicas.uis.edu.co
- Wikipedia. Somma di Riemann. Estratto da: es.wikipedia.com
- Wikipedia. Integrazione di Riemann. Estratto da: es.wikipedia.com



Nessun utente ha ancora commentato questo articolo.