
Proprietà, esempi ed esercizi di simmetria assiale
Il simmetria assiale Si verifica quando i punti di una figura coincidono con i punti di un'altra figura per mezzo di una bisettrice retta chiamata asse di simmetria. È anche chiamata simmetria radiale, rotazionale o cilindrica..
Di solito è applicato in figure geometriche, ma è facilmente osservabile in natura, poiché ci sono animali come farfalle, scorpioni, coccinelle o umani che presentano simmetria assiale..

Indice articolo
- 1 Come trovare la simmetria assiale
- 2 Proprietà della simmetria assiale
- 3 Esempi di simmetria assiale
- 4 esercizi di simmetria assiale
- 4.1 Esercizio 1
- 4.2 Esercizio 2
- 4.3 Esercizio 3
- 4.4 Esercizio 4
- 5 Riferimenti
Come trovare la simmetria assiale
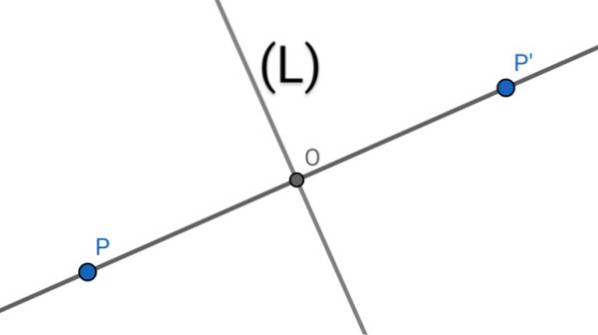
Per trovare la simmetria assiale P 'di un punto P rispetto ad una retta (L) si effettuano le seguenti operazioni geometriche:
1.- Si traccia la perpendicolare alla retta (L) che passa per il punto P..
2.- L'intercettazione delle due linee determina un punto O.
3.- Viene misurata la lunghezza del segmento PO, quindi questa lunghezza viene copiata sulla linea (PO) partendo da O nella direzione da P a O determinando il punto P '.
4.- Il punto P 'è la simmetria assiale del punto P rispetto all'asse (L), poiché la linea (L) è la mediatrice del segmento PP', dove O è il punto medio di detto segmento.
Proprietà della simmetria assiale
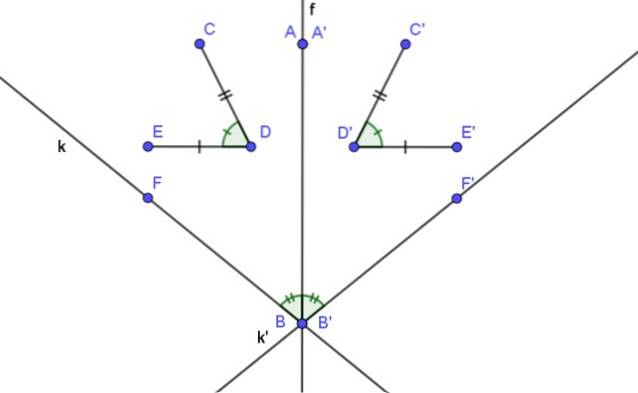
- La simmetria assiale è isometrica, ovvero le distanze di una figura geometrica e la sua simmetria corrispondente vengono preservate.
- La misura di un angolo e quella del suo simmetrico sono uguali.
- La simmetria assiale di un punto sull'asse di simmetria è il punto stesso.
- La linea simmetrica di una linea parallela all'asse di simmetria è anche una linea parallela a detto asse.
- Una linea secante rispetto all'asse di simmetria ha come linea simmetrica un'altra linea secante che, a sua volta, interseca l'asse di simmetria nello stesso punto della linea originale.
- L'immagine simmetrica di una linea è un'altra linea che forma un angolo con l'asse di simmetria della stessa misura di quella della linea originale.
- L'immagine simmetrica di una linea perpendicolare all'asse di simmetria è un'altra linea che si sovrappone alla prima.
- Una linea e la sua linea simmetrica assiale formano un angolo la cui bisettrice è l'asse di simmetria.
Esempi di simmetria assiale
La natura mostra abbondanti esempi di simmetria assiale. Ad esempio, puoi vedere la simmetria di volti, insetti come le farfalle, il riflesso su superfici di acque calme e specchi o le foglie delle piante, tra molti altri..


Esercizi di simmetria assiale
Esercizio 1
Abbiamo il triangolo dei vertici A, B e C le cui coordinate cartesiane sono rispettivamente A = (2, 5), B = (1, 1) e C = (3,3). Trova le coordinate cartesiane del triangolo simmetrico rispetto all'asse Y (asse delle ordinate).
Soluzione: Se un punto P ha coordinate (x, y), la sua simmetria rispetto all'asse delle ordinate (asse Y) è P '= (- x, y). Cioè, il valore della sua ascissa cambia segno, mentre il valore dell'ordinata rimane lo stesso.
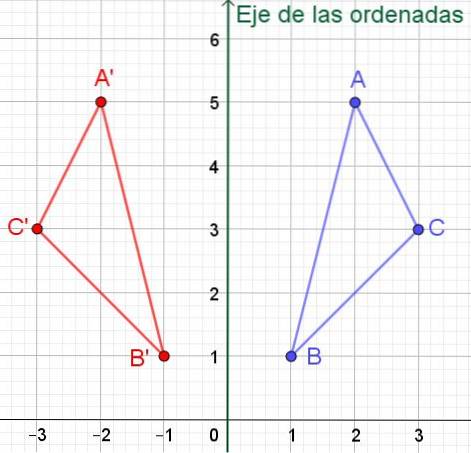
In questo caso, il triangolo simmetrico con vertici A ', B' e C 'avrà coordinate:
A '= (- 2, 5); B '= (- 1, 1) e C' = (- 3, 3) come si può vedere in figura 6.
Esercizio 2
Con riferimento al triangolo ABC e al suo simmetrico A'B'C 'dell'esercizio 1, verificare che i lati corrispondenti del triangolo originale e il suo simmetrico abbiano la stessa lunghezza.
Soluzione: Per trovare la distanza o la lunghezza dei lati usiamo la formula della distanza euclidea:
d (A, B) = √ ((Bx - Ax) ^ 2 + (By - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
La lunghezza del lato simmetrico corrispondente A'B 'è calcolata di seguito:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
In questo modo si verifica che la simmetria assiale preserva la distanza tra due punti. La procedura può essere ripetuta per gli altri due lati del triangolo e il suo simmetrico per verificare l'invarianza in lunghezza. Ad esempio | AC | = | A'C '| = √5 = 2.236.
Esercizio 3
In relazione al triangolo ABC e al suo simmetrico A'B'C 'dell'esercizio 1, verifica che gli angoli corrispondenti del triangolo originale e del suo simmetrico abbiano la stessa misura angolare.
Soluzione: Per determinare le misure degli angoli BAC e B'A'C ', verrà calcolato prima il prodotto scalare dei vettori AB con AC e poi il prodotto scalare di A'B ' con AC '.
Ricordando che:
A = (2, 5), B = (1, 1) e C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) e C' = (- 3, 3).
Esso ha:
AB = <1-2, 1-5> Y AC = <3-2, 3-5>
allo stesso modo
A'B ' = <-1+2, 1-5> Y AC = <-3+2, 3-5>
Quindi vengono trovati i seguenti prodotti scalari:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
Allo stesso modo
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
La misura dell'angolo BAC è:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅ |AC |)) =
ArcCos (7 / (4.123⋅2.236)) = 40,6º
Allo stesso modo, la misura dell'angolo B'A'C 'è:
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (|A'B '|⋅ |A'C '|)) =
ArcCos (7 / (4.123⋅2.236)) = 40,6º
Concludendo, la simmetria assiale preserva la misura dell'angolo.
Esercizio 4
Sia un punto P di coordinate (a, b). Trova le coordinate della sua simmetria assiale P 'rispetto alla linea y = x.
Soluzione: Chiameremo (a ', b') le coordinate del punto simmetrico P 'rispetto alla retta y = x. Il punto medio M del segmento PP 'ha coordinate ((a + a') / 2, (b + b ') / 2) ed è anche sulla linea y = x, quindi è vera la seguente uguaglianza:
a + a '= b + b'
D'altra parte, il segmento PP 'ha pendenza -1 perché è perpendicolare alla retta y = x con pendenza 1, quindi vale la seguente uguaglianza:
b - b '= a' -a
Risolvendo per le due precedenti uguaglianze a 'eb' si conclude che:
a '= be che b' = a.
Cioè, dato un punto P (a, b), la sua simmetria assiale rispetto alla retta y = x è P '(b, a).
Riferimenti
- Arce M., Blázquez S e altri. Trasformazioni dell'aereo. Estratto da: educutmxli.files.wordpress.com
- Calcolo cc. Simmetria assiale. Estratto da: calculo.cc
- Superprof. Simmetria assiale. Recupero da: superprof.es
- wikipedia. Simmetria assiale. Estratto da: es.wikipedia.com
- wikipedia. Simmetria circolare. Estratto da: en.wikipedia.com


Nessun utente ha ancora commentato questo articolo.