
Semicerchio come calcolare il perimetro, area, centroide, esercizi
Il semicerchio è una figura piana delimitata da un diametro della circonferenza e da uno dei due archi circolari piatti determinati da detto diametro.
In questo modo, un semicerchio è delimitato da a semicirconferenza, che consiste in un arco circolare piatto e un segmento rettilineo che unisce le estremità dell'arco circolare piatto. Il semicerchio racchiude il semicerchio e tutti i punti al suo interno..
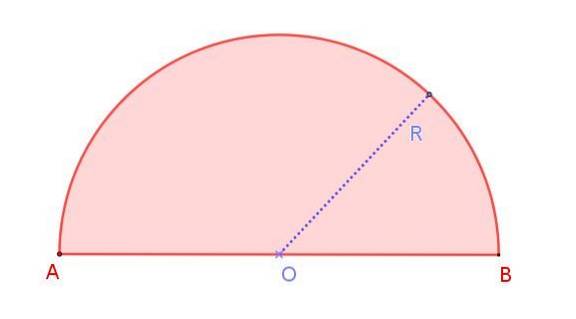
Possiamo vederlo nella figura 1, che mostra un semicerchio di raggio R, la cui misura è la metà di quella del diametro AB. Si noti che a differenza di un cerchio, in cui ci sono infiniti diametri, nella semicirconferenza c'è un solo diametro.
Il semicerchio è una figura geometrica con molti usi in architettura e design, come vediamo nell'immagine seguente:

Indice articolo
- 1 Elementi e misure di un semicerchio
- 1.1 Perimetro di un semicerchio
- 1.2 Area di un semicerchio
- 1.3 Centroide di un semicerchio
- 1.4 Momento d'inerzia di un semicerchio
- 1.5 Angolo inscritto
- 2 Esercizi risolti
- 2.1 Esercizio 1
- 2.2 Esercizio 2
- 2.3 Esercizio 3
- 2.4 Esercizio 4
- 2.5 Esercizio 5
- 3 Riferimenti
Elementi e misure di un semicerchio
Gli elementi di un semicerchio sono:
1.- L'arco circolare piano A⌒B
2.- Il segmento [AB]
3.- I punti all'interno del semicerchio composto dall'arco A⌒B e dal segmento [AB].
Perimetro di un semicerchio
Il perimetro è la somma del contorno dell'arco più quello del segmento retto, quindi:
Perimetro = lunghezza dell'arco A⌒B + lunghezza del segmento [AB]
Nel caso di un semicerchio di raggio R, il suo perimetro P sarà dato dalla formula:
P = π⋅R + 2⋅R = (π + 2) ⋅R
Il primo termine è la metà del perimetro di un cerchio di raggio R, mentre il secondo è la lunghezza del diametro, che è il doppio del raggio..
Area di un semicerchio
Poiché un semicerchio è uno dei settori angolari piani che rimangono quando si traccia un diametro attraverso la circonferenza, la sua area A sarà la metà dell'area del cerchio che contiene il semicerchio di raggio R:
A = (π⋅RDue) / 2 = ½ π⋅RDue
Centroide di un semicerchio
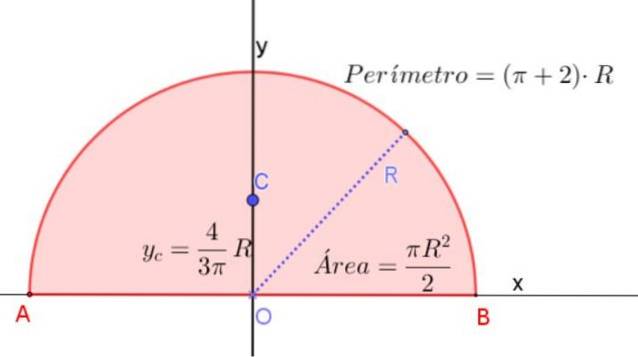
Il baricentro di un semicerchio è sul suo asse di simmetria ad un'altezza misurata dal suo diametro di 4 / (3π) volte il raggio R.
Ciò corrisponde a circa 0,424⋅R, misurato dal centro del semicerchio e sul suo asse di simmetria, come mostrato in figura 3.
Momento d'inerzia di un semicerchio
Il momento di inerzia di una figura piana rispetto ad un asse, ad esempio asse x, è definito come:
L'integrale del quadrato della distanza dei punti appartenenti alla figura rispetto all'asse, essendo il differenziale di integrazione un elemento di area infinitesimale, preso nella posizione di ogni punto.
La figura 4 mostra la definizione del momento d'inerzia IX del semicerchio di raggio R, rispetto all'asse X che passa per la sua diagonale:
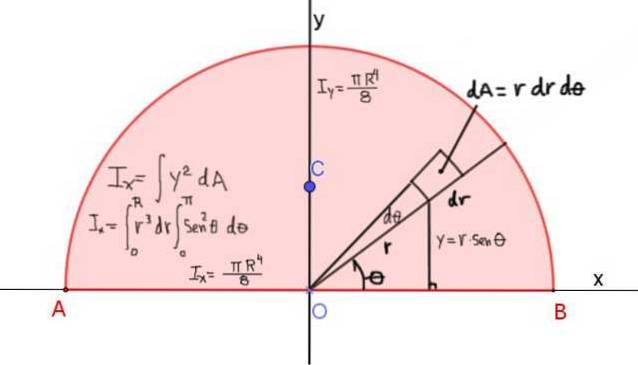
Il momento d'inerzia attorno all'asse x è dato da:
ioX = (π⋅R4) / 8
E il momento di inerzia rispetto all'asse di simmetria y è:
Iy = (π⋅R4) / 8
Si noti che entrambi i momenti di inerzia coincidono nella loro formula, ma è importante notare che si riferiscono ad assi diversi.
Angolo inscritto
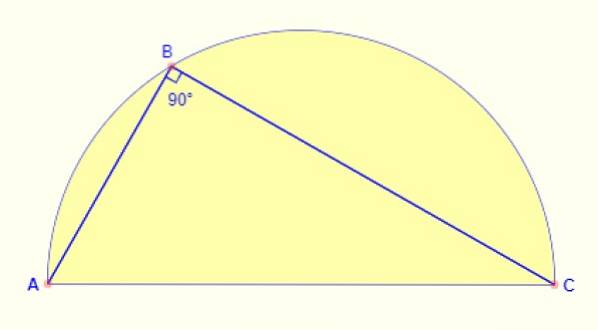
L'angolo inscritto nel semicerchio è sempre di 90º. Indipendentemente da dove viene preso il punto sull'arco, l'angolo formato tra i lati AB e BC della figura è sempre corretto..
Esercizi risolti
Esercizio 1
Determina il perimetro di un semicerchio di raggio 10 cm.
Soluzione
Ricorda che il perimetro in funzione del raggio è dato dalla formula che abbiamo visto in precedenza:
P = (2 + π) ⋅R
P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Esercizio 2
Trova l'area di un semicerchio con raggio di 10 cm.
Soluzione
La formula per l'area di un semicerchio è:
A = ½ π⋅RDue = ½ π⋅ (10 cm)Due = 50π cmDue = 50 x 3,14 cmDue = 157 cmDue.
Esercizio 3
Determinare l'altezza h del baricentro di un semicerchio di raggio R = 10 cm misurato dalla sua base, a parità di diametro del semicerchio.
Soluzione
Il baricentro è il punto di equilibrio del semicerchio e la sua posizione è sull'asse di simmetria ad un'altezza h dalla base (diametro del semicerchio):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm
Esercizio 4
Trova il momento d'inerzia di un semicerchio rispetto all'asse che coincide con il suo diametro, sapendo che il semicerchio è costituito da una lamina sottile. Il suo raggio è di 10 cm e la sua massa è di 100 grammi.
Soluzione
La formula che dà il momento d'inerzia del semicerchio è:
ioX = (π⋅R4) / 8
Ma poiché il problema ci dice che si tratta di un semicerchio materiale, allora la relazione precedente deve essere moltiplicata per la densità superficiale di massa del semicerchio, che sarà indicata con σ.
ioX = σ (π⋅R4) / 8
Procediamo quindi a determinare σ, che altro non è che la massa del semicerchio divisa per la sua area.
L'area è stata determinata nell'esercizio 2 e il risultato è stato di 157 cmDue. Quindi la densità superficiale di questo semicerchio sarà:
σ = 100 grammi / 157 cmDue = 0,637 g / cmDue
Quindi il momento d'inerzia rispetto al diametro verrà calcolato in questo modo:
ioX = (0,637 g / cmDue) [3,1416 ⋅ (10 cm)4] / 8
Risultante:
ioX = 2502 g⋅cmDue
Esercizio 5
Determinare il momento di inerzia di un semicerchio di raggio 10 cm costituito da un foglio di materiale con una densità superficiale di 0,637 g / cmDue lungo un asse che passa per il suo baricentro ed è parallelo al suo diametro.
Soluzione
Per risolvere questo esercizio è necessario ricordare il teorema di Steiner sui momenti di inerzia degli assi paralleli, che dice:
Il momento d'inerzia I rispetto ad un asse che si trova a distanza h dal baricentro è uguale alla somma del momento d'inerzia Ic rispetto ad un asse che passa per il baricentro ed è parallelo al primo più il prodotto della massa per il quadrato della separazione dei due assi.
Io = ioc + M hDue
Nel nostro caso è noto I quale è il momento d'inerzia rispetto al diametro, già calcolato nell'esercizio 4. È nota anche la distanza h tra il diametro e il baricentro, che è stata calcolata nell'esercizio 3.
Dobbiamo solo cancellare Ic:
ioc = I - M hDue
ioc = 2502 g⋅cmDue - 100 g ⋅ (4,246 cm)Due dando come risultato che il momento d'inerzia per un asse parallelo al diametro e passante per il baricentro è:
ioc = 699,15 g⋅cmDue
Riferimenti
- Alexander, D. 2013. Geometria. 5 °. Edizione. Cengage Learning.
- Math Open Reference. Semicerchio. Estratto da: mathopenref.com.
- Semicerchio delle formule dell'universo. Estratto da: universoformulas.com.
- Formule dell'universo. Area di un semicerchio. Estratto da: universoformulas.com.
- Wikipedia. Semicerchio. Estratto da: en.wikipedia.com.



Nessun utente ha ancora commentato questo articolo.