Quali tipi di integrali esistono?

Il tipi di integrali che troviamo nel calcolo sono gli integrali indefiniti e gli integrali definiti. Sebbene gli integrali definiti abbiano molte più applicazioni degli integrali indefiniti, è necessario prima imparare come risolvere gli integrali indefiniti..

Una delle applicazioni più interessanti degli integrali definiti è il calcolo del volume di un solido di rivoluzione. Entrambi i tipi di integrali hanno le stesse proprietà di linearità e anche le tecniche di integrazione non dipendono dal tipo di integrale.

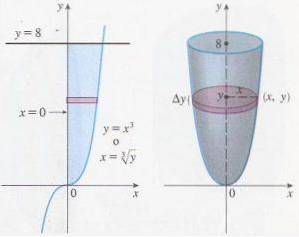
Ma nonostante siano molto simili, c'è una differenza principale; nel primo tipo di integrale il risultato è una funzione (che non è specifica) mentre nel secondo tipo il risultato è un numero.

Tipi fondamentali di integrali

Il mondo degli integrali è molto ampio, ma al suo interno possiamo distinguere due tipi fondamentali di integrali, che hanno grande applicabilità nella vita di tutti i giorni..

1- Integrali indefiniti

Se F '(x) = f (x) per ogni x nel dominio di f, diciamo che F (x) è un antiderivativo, una primitiva o un integrale di f (x).

D'altra parte, osserviamo che (F (x) + C) '= F' (x) = f (x), il che implica che l'integrale di una funzione non è unico, dato che dà valori diversi al costante C otterremo diversi antiderivativi.

Per questo motivo F (x) + C si chiama Integrale Indefinito di f (x) e C si chiama costante di integrazione e lo scriviamo come segue

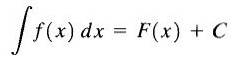
Come possiamo vedere, l'integrale indefinito della funzione f (x) è una famiglia di funzioni.

Ad esempio, se vuoi calcolare l'integrale indefinito della funzione f (x) = 3x², devi prima trovare una antiderivativa di f (x).

È facile vedere che F (x) = x³ è un antiderivativo, poiché F '(x) = 3x². Pertanto, si può concludere che

∫f (x) dx = ∫3x²dx = x³ + C.

2- Integrali definiti

Sia y = f (x) una funzione reale, continua su un intervallo chiuso [a, b] e sia F (x) un antiderivativo di f (x). L'integrale definito di f (x) tra i limiti aeb è chiamato numero F (b) -F (a), ed è indicato come segue

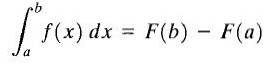
La formula mostrata sopra è meglio conosciuta come "Il teorema fondamentale del calcolo". Qui "a" è chiamato limite inferiore e "b" è chiamato limite superiore. Come puoi vedere, l'integrale definito di una funzione è un numero.

In questo caso, se calcoliamo l'integrale definito di f (x) = 3x² nell'intervallo [0,3], otterremo un numero.

Per determinare questo numero scegliamo F (x) = x³ come antiderivativo di f (x) = 3x². Quindi, calcoliamo F (3) -F (0) che ci dà il risultato 27-0 = 27. In conclusione, l'integrale definito di f (x) sull'intervallo [0,3] è 27.

Si può notare che se si sceglie G (x) = x³ + 3, allora G (x) è un antiderivativo di f (x) diverso da F (x), ma questo non influisce sul risultato poiché G (3) - G (0) = (27 + 3) - (3) = 27. Per questo negli integrali definiti non compare la costante di integrazione.

Una delle applicazioni più utili di questo tipo di integrale è che permette di calcolare l'area (volume) di una figura piana (di un solido di rivoluzione), stabilendo opportune funzioni e limiti di integrazione (e un asse di rotazione).

All'interno degli integrali definiti possiamo trovare varie estensioni di esso, come integrali di linea, integrali di superficie, integrali impropri, integrali multipli, tra gli altri, tutti con applicazioni molto utili nella scienza e nell'ingegneria..

Riferimenti

1. Casteleiro, J. M. (2012). È facile da integrare? Manuale di autoapprendimento. Madrid: ESIC.
2. Casteleiro, J. M. e Gómez-Álvarez, R. P. (2002). Calcolo integrale (Illustrato ed.). Madrid: editoriale ESIC.
3. Fleming, W., & Varberg, D.E. (1989). Precalculus Mathematics. Prentice Hall PTR.
4. Fleming, W., & Varberg, D.E. (1989). Matematica precalcolo: un approccio alla risoluzione dei problemi (2, illustrato ed.). Michigan: Prentice Hall.
5. Kishan, H. (2005). Calcolo integrale. Editori e distributori Atlantic.
6. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Calcolo (Nono ed.). Prentice Hall.