
Cosa sono i numeri triangolari? Proprietà e dimostrazioni

È noto come numeri triangolari alla sequenza di numeri che si ottengono facendo una disposizione o una figura di punti sotto forma di un triangolo equilatero. I primi della sequenza sono: 1, 3, 6, 10, 15, 21, ...
Il primo numero triangolare è 1, il secondo è 3, perché si ottiene sommando una riga di due punti a quella precedente, a formare un triangolo equilatero di tre elementi.
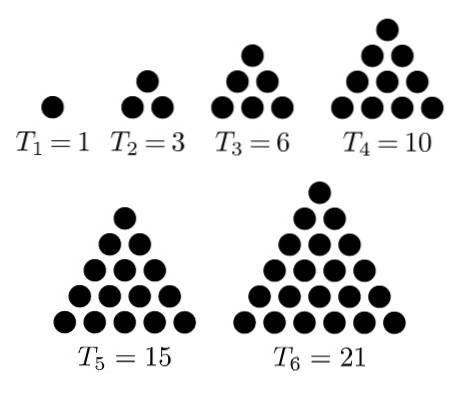
Il terzo è il 6, che appare quando si aggiunge una fila di tre punti alla disposizione precedente, in modo tale da formare un triangolo di tre punti per lato. Il 10 della sequenza si ottiene aggiungendo un'altra riga alla disposizione precedente in modo da formare un triangolo di quattro punti per lato.
La formula che permette di trovare l'elemento n della sequenza triangolare, noto il numero triangolare precedente è:
Tn = Tn-1 + n
L'elenco dei primi sei numeri triangolari si ottiene così:
-Primo: 1
-Secondo: 1 + 2 = 3
-Terzo: (1 +2) + 3 = 3 + 3 = 6
-Camera da letto: (1 + 2 + 3) + 4 = 6 + 4 = 10
-Quinto: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15
-Sesto: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21
Indice articolo
- 1 Proprietà dei numeri triangolari
- 2 Dimostrazioni
- 2.1 - Demo 1
- 2.2 - Demo 2
- 2.3 - Demo 3
- 2.4 - Dimostrazione 5
- 3 Riferimenti
Proprietà dei numeri triangolari
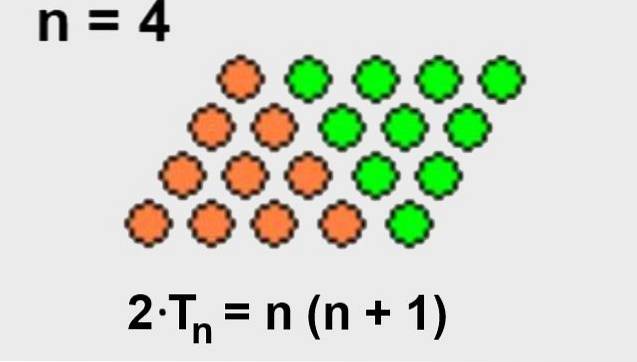
1.- L'n-esimo numero triangolare Tn della sequenza di numeri triangolari è la metà di n moltiplicato per n + 1:
Tn = ½ n (n + 1)
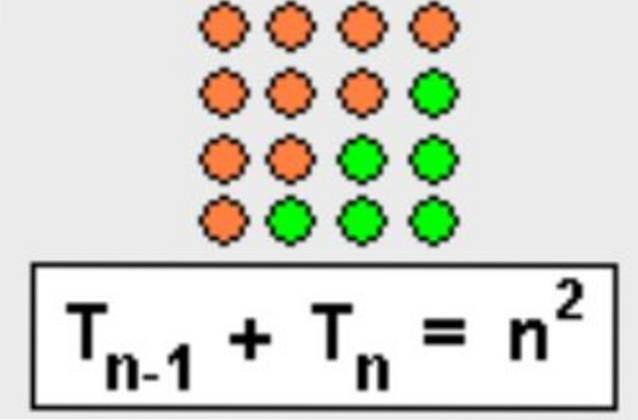
2.- La somma dell'n-esimo numero triangolare con il precedente numero triangolare, ovvero il (n-1) -esimo, è n al quadrato:
Tn + Tn-1= nDue
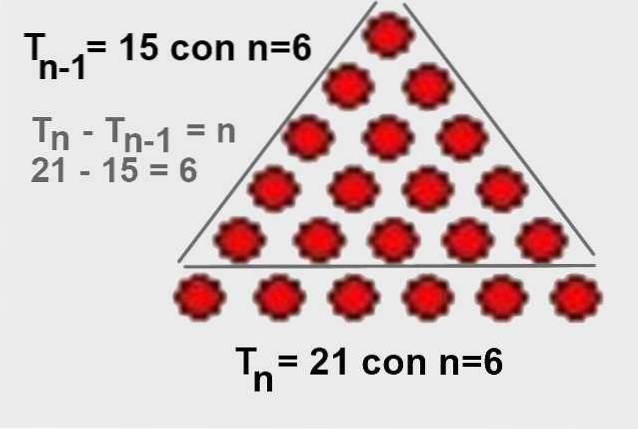
3.- La differenza tra l'n-esimo numero triangolare meno l'n-esimo numero triangolare meno uno è n:
Tn - Tn-1 = n
4.- La somma dei primi n numeri triangolari è chiamata numero tetraedrico Sn ed è uguale alla sesta parte del prodotto di n moltiplicato per (n + 1) e moltiplicato per (n + 2):
Sn= ⅙ n (n + 1) (n + 2)
5.- Ogni numero naturale N è il risultato della somma di tre numeri triangolari:
N = Δ1 + Δ1 + Δ3
Quest'ultima proprietà o teorema, fu scoperta dal grande matematico Carl Friedrich Gauss nel 1796, che annotò nel suo diario ponendo l'ammirazione greca Eureka! cosa significa "L'ho fatto".
Era la stessa parola usata molto tempo prima dal greco Archimede quando determinava il peso apparente di un corpo sommerso..
In questa relazione, il numero zero è considerato triangolare e può esserci ripetizione.
Dimostrazioni
- Demo 1
Dimostra che il numero triangolare n-Questo:
Tn = ½ n (n + 1)
È facile dedurre la formula sopra, se ci rendiamo conto che possiamo aggiungere un numero uguale di punti alla disposizione triangolare in modo che formi un quadrilatero di punti.
Poiché il numero totale di punti nella disposizione quadrilatera è il numero di righe n moltiplicato per il numero di colonne (n + 1), allora la disposizione triangolare avrà solo la metà dei punti della disposizione quadrilatera.
Qui è illustrato in figura 2.
- Demo 2
Mostra che la somma di n-numero del triangolo con il n-th meno uno il numero triangolare è n quadrato:
Tn + Tn-1= nDue
È già stato dimostrato che il numero triangolare n-è dato da:
Tn= ½ n (n + 1)
Pertanto, il numero triangolare sopra è:
Tn-1 = ½ (n-1) ((n-1) + 1) = ½ n (n - 1)
La somma di entrambi è:
Tn + Tn-1 = ½ n (n + 1) + ½ n (n - 1)
Si prende il fattore comune ½ n per ottenere:
Tn + Tn-1 = ½ n [(n + 1) + (n - 1)] = ½ n [n + 1 + n - 1]
E immediatamente l'espressione all'interno della parentesi è semplificata:
Tn + Tn-1 = ½ n [2 n] = ½ 2 n ⋅ n
Ora, ricordando che ½ per 2 è 1 e che n volte n è n quadrato, abbiamo:
Tn + Tn-1 = nDue
Questa proprietà può anche essere dimostrata in forma geometrica, basta completare il triangolo per formare un quadrato, come mostrato in figura 3.
- Demo 3
La differenza del numero d'ordine triangolare n meno il numero d'ordine triangolare n-1 è n:
Tn - Tn-1 = n
Ciò può essere dimostrato semplicemente ricordando che il seguente numero triangolare è ottenuto dal precedente utilizzando la formula:
Tn = Tn-1 + n
E da lì è evidente che Tn - Tn-1 = n. È anche facile visualizzarlo graficamente, come mostrato in figura 4.
- Demo 5
La somma dei primi n numeri triangolari Sn è uguale a un sesto del prodotto di n moltiplicato per (n + 1) e moltiplicato per (n + 2):
Sn = ⅙ n (n + 1) (n + 2)
Usiamo il numero triangolare di ordine n: Tn= ½ n (n + 1). La somma del primo n numeri triangolari lo indicano con Sn
Per esempio, S1 indica la somma del primo numero triangolare, che sarà senza dubbio 1.
Successivamente, vediamo se la formula che stiamo cercando di testare è vera per n = 1:
S1 = ⅙ 1⋅2⋅3 = 1
Infatti, la formula per n = 1 è verificata. È facile visualizzare che la somma dei primi n + 1 numeri triangolari sarà la somma del primo n più il successivo numero triangolare:
Sn + 1 = Sn + Tn + 1
Supponiamo ora che la formula per Sn è vero per n, quindi lo sostituiamo nell'espressione precedente e aggiungiamo il numero triangolare di ordine n + 1:
Sn + 1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]
Vediamo passo passo cosa ottieni:
-Eseguiamo la somma delle due espressioni frazionarie:
Sn + 1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] / 12
-È preso dal fattore comune del numeratore a 2 (n + 1) (n + 2) e semplifica:
Sn + 1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6
Il risultato di cui sopra concorda con la formula per Sn se n è sostituito da n + 1, che è stata mostrata per induzione la formula per la somma dei primi n termini triangolari.
Numero tetraedrico
Viene chiamato il risultato così ottenuto numero tetraedrico dell'ordine n, perché è come accumulare strati triangolari che formano un tetraedro, come mostrato nell'animazione seguente.

Riferimenti
- Camacho J. Un'apparizione inaspettata di numeri triangolari. Estratto da: masscience.com
- Claudio. Numeri triangolari. Recupero da: semplicemente numeri. blogspot. com
- Wikipedia. Numero triangolare. Estratto da: es.wikipedia.com
- Wikipedia. Numero triangolare. Estratto da: en.wikipedia.com
- Wikipedia. Numero tretraedrico. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.