
Definizione poligono convesso, elementi, proprietà, esempi

UN poligono convesso è una figura geometrica contenuta in un piano che si caratterizza perché ha tutte le sue diagonali al suo interno e i suoi angoli misurano meno di 180º. Tra le sue proprietà ci sono le seguenti:
1) Consiste di n segmenti consecutivi dove l'ultimo dei segmenti si unisce al primo. 2) Nessuno dei segmenti si interseca in modo tale da delimitare il piano in una regione interna e in una regione esterna. 3) Ogni angolo nella regione interna è strettamente minore di un angolo piano.

Un modo semplice per determinare se un poligono è convesso o meno è considerare la linea che passa per uno dei suoi lati, che determina due semipiani. Se in ogni linea che passa per un lato, gli altri lati del poligono si trovano sullo stesso semipiano, allora è un poligono convesso.
Indice articolo
- 1 Elementi di un poligono
- 1.1 Poligoni convessi e non convessi
- 2 Proprietà del poligono convesso
- 2.1 Diagonali e angoli in poligoni convessi
- 3 esempi
- 3.1 Esempio 1
- 3.2 Esempio 2
Elementi di un poligono
Ogni poligono è costituito dai seguenti elementi:
- Lati
- Vertici
I lati sono ciascuno dei segmenti consecutivi che compongono il poligono. In un poligono nessuno dei segmenti che lo compongono può avere un'estremità aperta, in quel caso ci sarebbe una linea poligonale ma non un poligono.
I vertici sono i punti di giunzione di due segmenti consecutivi. In un poligono, il numero di vertici è sempre uguale al numero di lati.
Se due lati o segmenti di un poligono si intersecano, si ha un poligono incrociato. Il punto di incrocio non è considerato un vertice. Un poligono trasversale è un poligono non convesso. I poligoni a stella sono poligoni incrociati e quindi non sono convessi.
Quando un poligono ha tutti i lati della stessa lunghezza, allora abbiamo un poligono regolare. Tutti i poligoni regolari sono convessi.
Poligoni convessi e non convessi
La figura 1 mostra diversi poligoni, alcuni di essi sono convessi e altri no. Analizziamoli:
Il numero 1 è un poligono a tre lati (triangolo) e tutti gli angoli interni sono inferiori a 180º, quindi è un poligono convesso. Tutti i triangoli sono poligoni convessi.
Il numero 2 è un poligono a quattro lati (quadrilatero) in cui nessuno dei lati si interseca e ogni angolo interno è inferiore a 180º. È quindi un poligono convesso con quattro lati (quadrilatero convesso).
D'altra parte, il numero 3 è un poligono con quattro lati ma uno dei suoi angoli interni è maggiore di 180º, quindi non soddisfa la condizione di convessità. Cioè, è un poligono a quattro lati non convesso chiamato quadrilatero concavo..
Il numero 4 è un poligono con quattro segmenti (lati), due dei quali si intersecano. I quattro angoli interni sono inferiori a 180º, ma poiché due lati si intersecano, si tratta di un poligono incrociato non convesso (quadrilatero incrociato).
Un altro caso è il numero 5. Questo è un poligono a cinque lati, ma poiché uno dei suoi angoli interni è maggiore di 180º, abbiamo un poligono concavo.
Infine, il numero 6, che ha anche cinque lati, ha tutti i suoi angoli interni inferiori a 180º, quindi è un poligono convesso con cinque lati (pentagono convesso).
Proprietà del poligono convesso
1- Un poligono non incrociato o un poligono semplice divide il piano che lo contiene in due regioni. La regione interna e la regione esterna, essendo il poligono il confine tra le due regioni.
Ma se in aggiunta il poligono è convesso, allora abbiamo una regione interna che è semplicemente connessa, il che significa che prendendo due punti qualsiasi dalla regione interna, può sempre essere unita da un segmento che appartiene interamente alla regione interna..
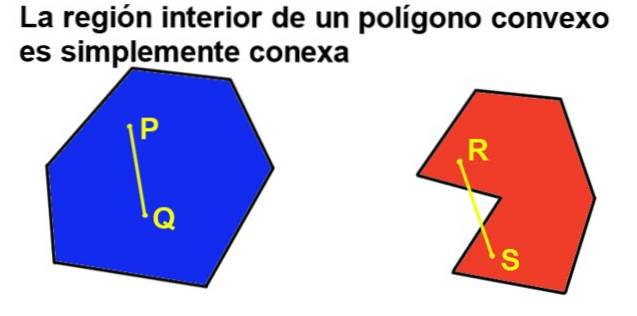
2- Ogni angolo interno di un poligono convesso è inferiore a un angolo piano (180º).
3- Tutti i punti interni di un poligono convesso appartengono sempre ad uno dei semipiani definiti dalla linea che passa per due vertici consecutivi.
4- In un poligono convesso tutte le diagonali sono totalmente contenute nella regione poligonale interna.
5- I punti interni di un poligono convesso appartengono interamente al settore angolare convesso definito da ciascun angolo interno.
6- Ogni poligono in cui tutti i suoi vertici sono su una circonferenza è un poligono convesso che è chiamato poligono ciclico.
7- Ogni poligono ciclico è convesso, ma non tutti i poligoni convessi sono ciclici.
8- Qualsiasi poligono non incrociato (poligono semplice) che ha tutti i lati di uguale lunghezza è convesso ed è noto come poligono regolare.
Diagonali e angoli in poligoni convessi
9- Il numero totale N di diagonali di un poligono convesso con n lati è dato dalla seguente formula:
N = ½ n (n - 3)
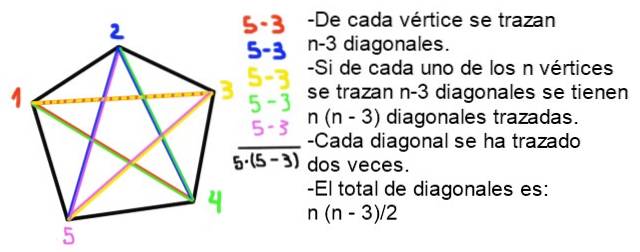
Dimostrazione: In un poligono convesso con n lati di ciascun vertice, vengono disegnate n - 3 diagonali, poiché il vertice stesso e i due adiacenti sono esclusi. Poiché ci sono n vertici, vengono disegnate n (n - 2) diagonali in totale, ma ciascuna diagonale è stata disegnata due volte, quindi il numero di diagonali (senza ripetizione) è n (n-2) / 2.
10- La somma S degli angoli interni di un poligono convesso di n lati è data dalla seguente relazione:
S = (n - 2) 180º
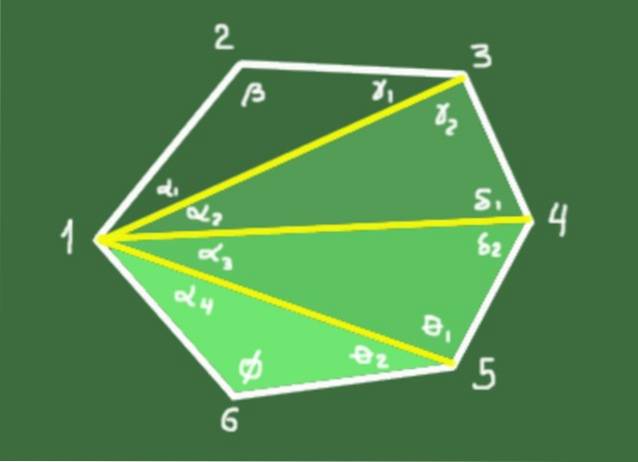
Dimostrazione: da un vertice vengono disegnate n-3 diagonali che definiscono n-2 triangoli. La somma degli angoli interni di ogni triangolo è 180º. La somma totale degli angoli degli n-2 triangoli è (n-2) * 180º, che coincide con la somma degli angoli interni del poligono.
Esempi
Esempio 1
L'esagono ciclico, è un poligono con sei lati e sei vertici, ma tutti i vertici sono sulla stessa circonferenza. Ogni poligono ciclico è convesso.
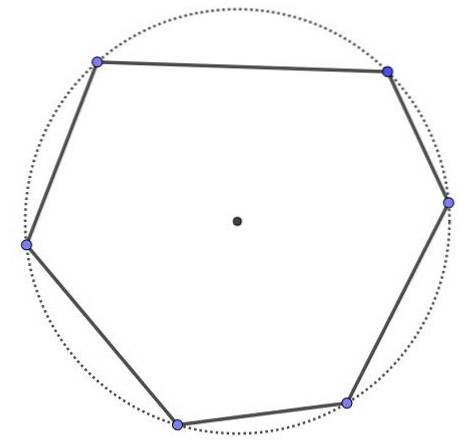
Esempio 2
Determina il valore degli angoli interni di un enegon regolare.
Soluzione: L'enegon è un poligono a 9 lati, ma se è anche regolare, tutti i suoi lati e angoli sono uguali.
La somma di tutti gli angoli interni di un poligono a 9 lati è:
S = (9 - 2) 180º = 7 * 180º = 1260º
Ma ci sono 9 angoli interni di uguale misura α, quindi la seguente uguaglianza deve essere soddisfatta:
S = 9 α = 1260º
Da cui segue che la misura α di ogni angolo interno dell'enegone regolare è:
α = 1260º / 9 = 140º

Nessun utente ha ancora commentato questo articolo.