
Numeri perfetti come identificarli ed esempi

UN numero perfetto è un numero naturale tale che la somma dei suoi divisori è uguale al numero. Ovviamente il numero stesso non può essere compreso tra i divisori.
Uno degli esempi più semplici di un numero perfetto è 6, poiché i suoi divisori sono: 1, 2 e 3. Se sommiamo i divisori, otteniamo: 1 + 2 + 3 = 6.
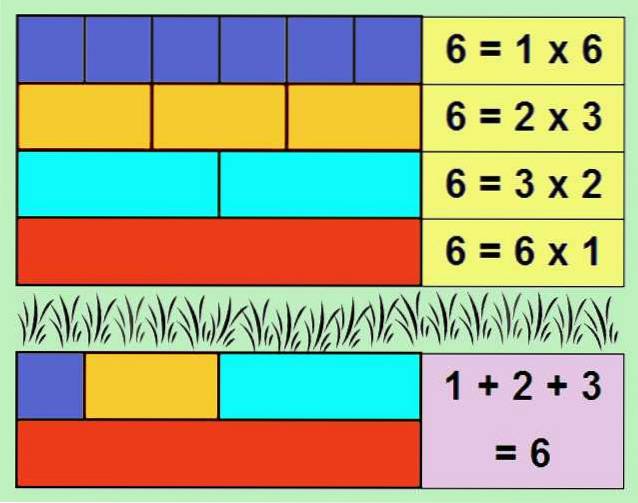
Viene chiamata la somma dei divisori di un intero, escluso il numero stesso aliquota. Quindi un numero perfetto è uguale alla sua aliquota.
Ma se il numero stesso è incluso nella somma dei divisori di un numero, allora un numero perfetto sarà quello in cui la somma di tutti i suoi divisori divisa per 2 è uguale al numero stesso..
Indice articolo
- 1 Storia
- 2 Proprietà dei numeri perfetti
- 2.1 Formula e criterio di Euclide
- 2.2 Il più grande numero perfetto conosciuto
- 2.3 Un numero perfetto è amico di se stesso
- 3 Esempi di numeri perfetti
- 4 esercizi
- 4.1 - Esercizio 1
- 4.2 - Esercizio 2
- 4.3 - Esercizio 3
- 4.4 - Esercizio 4
- 5 Riferimenti
Storia
I matematici dell'antichità, in particolare i greci, attribuivano grande importanza ai numeri perfetti e attribuivano loro qualità divine..
Ad esempio, Filone d'Alessandria, verso il I secolo, affermò che 6 e 28 sono numeri perfetti che coincidono con i sei giorni della creazione del mondo e con i ventotto giorni che la Luna impiega per fare il giro della Terra..
I numeri perfetti sono presenti anche in natura, ad esempio al polo nord di Saturno compare anche il numero perfetto 6, un vortice di forma esagonale trovato dalla sonda Cassini e che ha incuriosito gli scienziati..
I favi delle api hanno celle a forma esagonale, cioè con 6 lati. È stato dimostrato che il poligono con il numero perfetto 6 è quello che permette di massimizzare il numero di cellule dell'alveare, con il minimo di cera per la sua elaborazione..

Proprietà dei numeri perfetti
La somma di tutti i divisori di un numero naturale n è indicata con σ (n). In un numero perfetto si verifica che: σ (n) = 2n.
Formula e criteri di Euclide
Euclide ha scoperto una formula e un criterio che permette di trovare i numeri perfetti. Questa formula è:
Due(n-1) (Duen -1)
Tuttavia, il numero generato dalla formula sarà perfetto solo quando il fattore (2n -1) essere un cugino.
Vediamo come vengono generati i primi numeri perfetti:
Se n = 2, ci rimane 21 (DueDue - 1) = 2 x 3 = 6 che abbiamo già visto è perfetto.
Quando n = 3 abbiamo 2Due (Due3 - 1) = 4 x 7 = 28 che è anche perfetto come verificato in dettaglio nell'esempio 1.
Vediamo cosa succede con n = 4. Quando si sostituisce nella formula di Euclide abbiamo:
Due3 (Due4 - 1) = 8 x 15 = 120
Si può verificare che questo numero non è perfetto, come mostrato in dettaglio nell'Esempio 3. Ciò non contraddice il criterio di Euclide, poiché 15 non è primo, requisito necessario affinché il risultato sia un numero perfetto.
Vediamo ora cosa succede quando n = 5. Applicando la formula abbiamo:
Due4 (Due5 - 1) = 16 x 31 = 496
Poiché 31 è un numero primo, il numero 496 deve essere perfetto, secondo i criteri di Euclide. Nell'esempio 4 è mostrato in dettaglio che lo è davvero.
Numeri primi che hanno la forma 2p - 1 sono chiamati cugini Mersenne, dal nome del monaco Marin Mersenne, che studiò numeri primi e numeri perfetti nel XVII secolo..
Più tardi, nel XVIII secolo, Leonhard Euler dimostrò che tutti i numeri perfetti generati dalla formula di Euclide sono pari.
Ad oggi non è stato trovato alcun perfetto che sia strano.
Il numero perfetto più grande conosciuto
Ad oggi si conoscono 51 numeri perfetti, tutti generati dalla formula e dal criterio di Euclide. Questo numero è stato ottenuto una volta trovato il cugino Mersenne più grande, che è: (282589933 - 1).
Il numero perfetto # 51 è (282589933) x (282589933 - 1) e ha 49724095 cifre.
Un numero perfetto è amico di se stesso
Nella teoria dei numeri si dice che due numeri sono amici quando la somma dei divisori di uno, escluso il numero stesso, è uguale all'altro numero e viceversa.
Il lettore può verificare che la somma dei divisori di 220, escluso 220 è 284. D'altra parte, la somma dei divisori di 284, escluso 284, è uguale a 220. Pertanto la coppia di numeri 220 e 284 sono amici.
Da questo punto di vista, un numero perfetto è amico di se stesso..
Esempi di numeri perfetti
I primi otto numeri perfetti sono elencati di seguito:
6
28
496
8128
33550336
8589869056
137438691328
2305843008139952128
Formazione
Negli esercizi seguenti sarà necessario calcolare i divisori di un numero, per poi sommarli e verificare se il numero è un numero perfetto oppure no..
Pertanto, prima di affrontare gli esercizi, esamineremo il concetto e mostreremo come vengono calcolati..
Per cominciare, devi ricordare che i numeri possono essere primi (quando possono essere divisi esattamente solo con se stesso e 1) o composti (quando possono essere scomposti come un prodotto di numeri primi).
Per un numero composto N abbiamo:
N = an . bm. cp ... rK
Dove a, b, c ... r sono numeri primi e n, m, p ... k sono esponenti appartenenti ai numeri naturali, che possono essere da 1 in poi.
In termini di questi esponenti, esiste una formula per sapere quanti divisori ha il numero N, anche se non ci dice cosa siano. Sia C questa quantità, quindi:
C = (n +1) (m + 1) (p +1)… (k + 1)
Decomporre il numero N come prodotto di numeri primi e sapere quanti divisori ha, sia primi che non primi, ci aiuterà a determinare quali sono questi divisori..
Una volta che li hai tutti, tranne l'ultimo che non è richiesto nella somma, puoi verificare se è un numero perfetto o meno.
- Esercizio 1
Verifica che il numero 28 sia perfetto.
Soluzione
La prima cosa sarà scomporre il numero nei suoi fattori primi.
28 | 2
14 | 2
07 | 7
01 | 1
I suoi divisori sono: 1, 2, 4, 7, 14 e 28. Se escludiamo 28, la somma dei divisori dà:
1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28
Quindi 28 è un numero perfetto.
Inoltre, la somma di tutti i suoi divisori è 28 + 28 quindi la regola σ (28) = 2 x 28 è soddisfatta.
- Esercizio 2
Decidere se il numero 38 è perfetto o no.
Soluzione
Il numero è scomposto nei suoi fattori primi:
39 | 3
13 | 13
01 | 1
I divisori di 39 senza includere il numero stesso sono: 1, 3 e 13. La somma 1 + 3 + 13 = 4 + 13 = 17 non è uguale a 39, quindi 39 è un numero imperfetto o non perfetto.
- Esercizio 3
Scopri se il numero 120 è perfetto o imperfetto.
Soluzione
Procediamo a scomporre il numero nei suoi fattori primi:
120 | 2
060 | 2
30 | 2
15 | 3
5 | 5
1 | 1
Dai fattori primi procediamo per trovare i divisori:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 e 120
Se 120 fosse perfetto, sommando tutti i suoi divisori si otterrebbe 2 x 120 = 240.
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360
Questo risultato è chiaramente diverso da 240, quindi si conclude che il numero 120 non è un numero perfetto..
- Esercizio 4
Verifica che il numero 496, ottenuto con il criterio di Euclide, sia un numero perfetto.
Soluzione
Il numero 496 è scomposto nei suoi fattori primi:
496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1
Quindi i suoi divisori sono:
1, 2, 4, 8, 16, 31, 62, 124, 248, 496
Ora vengono aggiunti tutti, tranne 496:
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Confermando che è davvero un numero perfetto.
Riferimenti
- Baldor, A. 1986. Aritmetica. Edizioni e distribuzioni del Codex.
- Tutto sui numeri primi. Numeri amichevoli. Estratto da: numeroprimos.org.
- Wolfram MathWorld. Regola di Eulero. Estratto da: mathworld.wolfram.com.
- Wolfram MathWorld. Numero perfetto. Estratto da: mathworld.wolfram.com.
- Wikipedia. Numeri perfetti. Estratto da: en.wikipedia.org.
- Wikipedia. Numeri amichevoli. Estratto da: es.wikipedia.org.


Nessun utente ha ancora commentato questo articolo.