
Angoli opposti al vertice (con esercizio risolto)
Il Angoli opposti dal vertice sono quelli che soddisfano quanto segue: i lati di uno di essi sono le estensioni dei lati dell'altro angolo. Il teorema fondamentale degli angoli opposti al vertice dice così: due angoli opposti al vertice hanno la stessa misura.
Il linguaggio è spesso abusato dicendo che gli angoli opposti al vertice sono uguali, il che non è corretto. Solo perché due angoli hanno la stessa misura non significa che siano uguali. È come dire che due bambini della stessa altezza sono uguali.
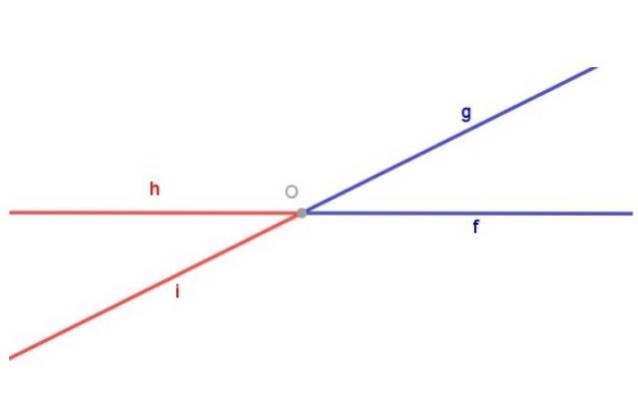
Ricordiamo che un angolo è definito come la figura geometrica composta da due raggi con la stessa origine.
La figura 1 mostra l'angolo nebbia (blu) composto dal raggio [Di) e il raggio [Og) di origine comune O. La figura 1 mostra anche l'angolo Hoi (rosso) composto dal raggio [Ho sentito) e il raggio [Oh) entrambi con origine O.
Due angoli contrapposti al vertice sono due diverse figure geometriche. Per evidenziarlo, nella figura 1 l'angolo è stato colorato nebbia blu, mentre l'angolo Hoi è stato colorato di rosso.
Gli angoli blu e rosso nella Figura 1 sono opposti al vertice perché: il raggio [Di) dell'angolo blu è il prolungamento del raggio [Oh) dell'angolo rosso e del raggio [Og) dell'angolo blu è il prolungamento del raggio [Ho sentito) dell'angolo rosso.
Indice articolo
- 1 Concetti importanti sugli angoli
- 1.1 Lati e vertici di un angolo
- 1.2 Angoli formati da due linee intersecanti
- 2 Linee perpendicolari e angolo retto
- 2.1 Raggi sulla stessa linea e angolo piano
- 2.2 Angolo nullo e angolo completo
- 3 Misurazione dell'angolo
- 3.1 Sistema sessagesimale
- 4 Teorema degli angoli di vertice
- 4.1 Demo
- 5 Esercizio risolto
- 5.1 Soluzione
- 6 Riferimenti
Concetti importanti sugli angoli
Lati e vertici di un angolo
La figura geometrica che consiste di due raggi con origine comune è un angolo. L'immagine seguente mostra l'angolo POQ formato dai due raggi [OPERAZIONE) Y [OQ) di origine comune O:
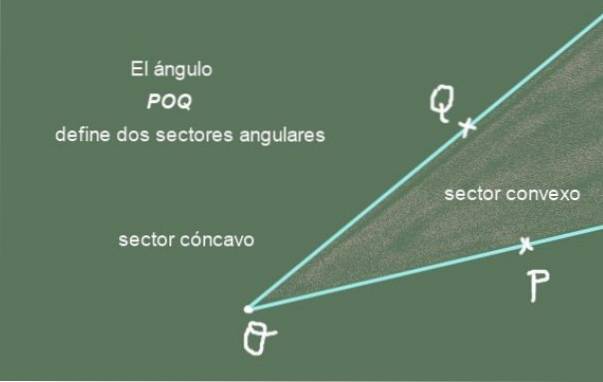
I raggi [OPERAZIONE) Y [OQ) sono i lati ad angolo POQ, mentre il punto comune O è chiamato vertice dell'angolo.
Settore angolare: Un angolo divide il piano che lo contiene in due settori angolari. Uno di questi è il settore angolare convesso e l'altro è il settore angolare concavo. L'unione dei due settori dà il piano completo.
La figura 2 mostra l'angolo POQ e i suoi due settori angolari. Il settore angolare convesso è quello di forma appuntita, mentre il concavo è il settore angolare del piano a cui manca il settore convesso.
Angoli formati da due linee che si intersecano
Due linee intersecanti di un piano formano quattro angoli e dividono il piano in quattro settori angolari.
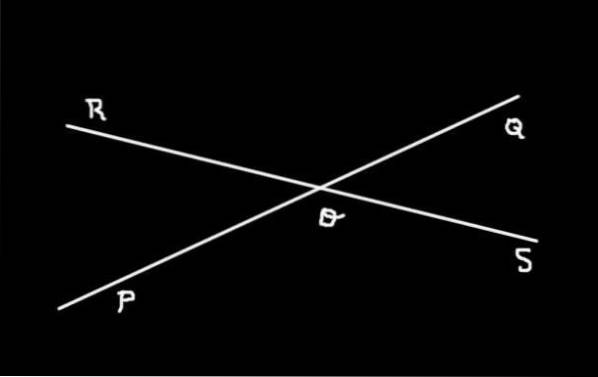
La figura 3 mostra le due linee (PQ) Y (RS) che vengono intercettati in O. Lì si può vedere che vengono determinati quattro angoli:
-SOQ, QOR, ROP Y POS
Gli angoli SOQ Y QOR, QOR Y ROP, ROP Y POS, POS Y SOQ Sono angoli adiacenti l'un l'altro, mentre SOQ Y ROP sono opposti al vertice. Sono anche Angoli opposti dal vertice Gli angoli QOR Y POS.
Linee perpendicolari e angoli retti
Due linee secanti (linee intersecanti) sono Linee rette perpendicolari se determinano quattro settori angolari di uguale misura. Se ciascuno dei quattro settori è simmetrico con il settore angolare adiacente, allora hanno la stessa misura.
Ciascuno degli angoli che determinano le due linee perpendicolari è chiamato angolo retto. Tutti gli angoli retti hanno la stessa misura.
Raggi sulla stessa linea e angolo del piano
Data una linea e un punto su di essa, vengono definiti due raggi. Quei due raggi ne definiscono due angoli piani.
Nella figura 3 puoi vedere la linea (RS) e il punto O che appartiene a (RS). L'angolo SOR è un angolo piano. Si può anche affermare che l'angolo ROS è un angolo piano. Tutti gli angoli piani hanno la stessa misura.
Angolo nullo e angolo completo
Un unico raggio definisce due angoli: uno dei quali quello del settore angolare convesso è il angolo nullo e l'altro, quello del settore angolare concavo è il angolo pieno. Nella figura 3 puoi vedere il file angolo nullo sos e il angolo pieno sos.
Misurazione dell'angolo
Esistono due sistemi numerici che vengono utilizzati frequentemente per fornire la misura di un angolo.
Uno di questi è il sistema sessagesimale, cioè basato sul numero 60. È un'eredità delle antiche culture mesopotamiche. L'altro sistema di misurazione dell'angolo è il sistema radiante, basato sul numero π (pi) ed è un'eredità degli antichi saggi greci che hanno sviluppato la geometria.
Sistema sessagesimale
Angolo nullo: nel sistema sessagesimale l'angolo nullo misura 0º (zero gradi).
Angolo completo: gli viene assegnata la misura 360º (trecentosessanta gradi).
Angolo piano: nel sistema sessagesimale l'angolo del piano misura 180º (centottanta gradi).
Angolo retto: due linee perpendicolari dividono il piano in quattro angoli di uguale misura chiamati angoli retti. La misura di un angolo retto è la quarta parte dell'angolo completo, vale a dire 90º (novanta gradi).
Goniometro o goniometro
Il goniometro è lo strumento utilizzato per misurare gli angoli. Consiste in un semicerchio (solitamente plastica trasparente) diviso in 180 sezioni angolari. Poiché un semicerchio forma un angolo piano, la misura tra due sezioni consecutive è 1º.
Il goniometro è simile al goniometro ed è costituito da un cerchio diviso in 360 sezioni angolari.
Un angolo i cui lati iniziano dal centro del goniometro intersecano due settori e la misura di quell'angolo in gradi è uguale al numero n di sezioni tra i due settori intercettati, in questo caso la misura sarà nº (si legge "Jan gradi").
Teorema degli angoli dei vertici
Formalmente, il teorema è affermato in questo modo:
Se due angoli sono verticalmente opposti, hanno la stessa misura.
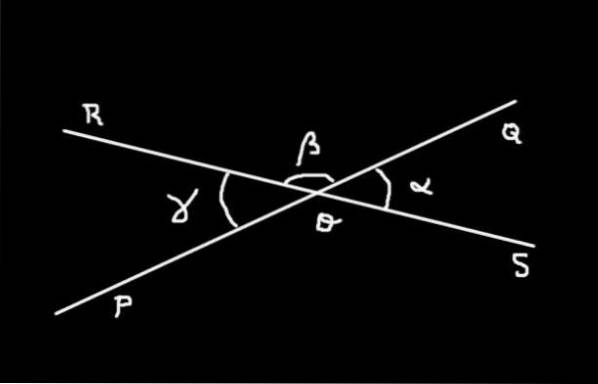
Dimostrazione
L'angolo SOQ ha misura α; l'angolo QOR ha misura β e angolo ROP ha misura γ. La somma dell'angolo SOQ più lui QOR formano l'angolo del piano SOR misura 180º.
Questo è:
α + β = 180º
D'altra parte e usando lo stesso ragionamento con gli angoli QOR Y ROP avete:
β + γ = 180º
Se osserviamo le due equazioni precedenti, l'unico modo in cui sono soddisfatte entrambe è che α è uguale a γ.
Che cosa SOQ ha misura α ed è opposta dal vertice a ROP di misura γ, e poiché α = γ, si conclude che gli angoli opposti al vertice hanno la stessa misura.
Esercizio risolto
Facendo riferimento alla Figura 4: Supponiamo che β = 2 α. Trova la misura degli angoli SOQ, QOR Y ROP in gradi sessagesimali.
Soluzione
Come la somma dell'angolo SOQ più lui QOR formano l'angolo del piano SOR avete:
α + β = 180º
Ma ci dicono che β = 2 α. Sostituendo questo valore di β abbiamo:
α + 2 α = 180º
Vale a dire:
3 α = 180º
Il che significa che α è la terza parte di 180º:
α = (180º / 3) = 60º
Quindi la misura di SOQ è α = 60º. La misura di QOR è β = 2 α = 2 * 60º = 120º. Finalmente piace ROP è opposto per vertice a SOQ quindi secondo il già provato teorema hanno la stessa misura. Cioè, la misura di ROP è γ = α = 60º.
Riferimenti
- Baldor, J. A. 1973. Plane and Space Geometry. Centro culturale americano.
- Leggi e formule matematiche. Sistemi di misura angolari. Estratto da: ingemecanica.com.
- Wikipedia. Angoli opposti dal vertice. Estratto da: es.wikipedia.com
- Wikipedia. Trasportatore. Estratto da: es.wikipedia.com
- Zapata F. Goniómetro: storia, parti, operazione. Estratto da: lifeder.com


Nessun utente ha ancora commentato questo articolo.