
Misure di posizione, tendenza centrale e dispersione
Il misure di tendenza centrale, dispersione e posizione, sono valori che vengono utilizzati per interpretare correttamente un insieme di dati statistici. Questi possono essere lavorati direttamente, in quanto ottenuti dallo studio statistico, oppure possono essere organizzati in gruppi di uguale frequenza, facilitando l'analisi..
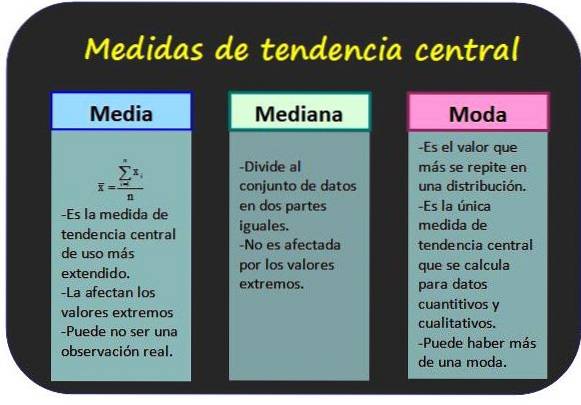
Misure di tendenza centrale
Consentono di sapere attorno a quali valori sono raggruppati i dati statistici.
Media aritmetica
È anche nota come media dei valori di una variabile e si ottiene sommando tutti i valori e dividendo il risultato per il numero totale di dati.
-
Media aritmetica per dati non raggruppati
Sia una variabile x di cui abbiamo n dati senza organizzare o raggruppare, la sua media aritmetica si calcola come segue:

E in notazione sommatoria:

Esempio
I proprietari di un agriturismo di montagna hanno intenzione di sapere quanti giorni mediamente i visitatori trascorrono nelle strutture. Per questo è stata tenuta una registrazione dei giorni di permanenza di 20 gruppi di turisti, ottenendo i seguenti dati:
1; 1; Due; Due; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; Due; Due; 3; 4; 1
Il numero medio di giorni di permanenza dei turisti è:

-
Media aritmetica per dati raggruppati
Se i dati della variabile sono organizzati in una tabella di frequenze assolute fio e i centri di classe sono x1, XDue,..., Xn, la media è calcolata da:

In notazione sommatoria:

Mediano
La mediana di un gruppo di n valori della variabile x è il valore centrale del gruppo, a condizione che i valori siano ordinati in ordine crescente. In questo modo, metà di tutti i valori è inferiore alla modalità e l'altra metà è maggiore..
-
Mediana dei dati non raggruppati
Possono verificarsi i seguenti casi:
-Numero n di valori della variabile x dispari: la mediana è il valore che si trova proprio al centro del gruppo di valori:

-Numero n di valori della variabile x paio: in questo caso la mediana è calcolata come media dei due valori centrali del gruppo di dati:

Esempio
Per trovare la mediana dei dati dell'ostello turistico, vengono prima ordinati dal più basso al più alto:
1; 1; 1; 1; 1; 1; 1; Due; Due; Due; Due; 3; 3; 3; 4; 4; 4; 4; 5; 5
Il numero di dati è pari, quindi ci sono due dati centrali: X10 e Xundici e poiché entrambi valgono 2, anche la loro media è.
Mediana = 2
-
Mediana dei dati aggregati
Viene utilizzata la seguente formula:

I simboli nella formula significano:
-c: larghezza dell'intervallo che contiene la mediana
-BM: limite inferiore dello stesso intervallo
-Fm: numero di osservazioni contenute nell'intervallo a cui appartiene la mediana.
-n: dati totali.
-FBM: numero di osservazioni prima dell'intervallo contenente la mediana.
moda
La modalità per i dati non raggruppati è il valore con la frequenza più alta, mentre per i dati raggruppati è la classe con la frequenza più alta. La moda è considerata il dato o la classe di distribuzione più rappresentativa.
Due caratteristiche importanti di questa misura è che un set di dati può avere più di una modalità e la modalità può essere determinata sia per i dati quantitativi che per quelli qualitativi..
Esempio
Continuando con i dati del parador turistico, quello che si ripete di più è 1, quindi la cosa più comune è che i turisti stiano 1 giorno nel parador.
Misure di dispersione
Le misure di dispersione descrivono il grado di raggruppamento dei dati attorno alle misure centrali.
Rango
Viene calcolato sottraendo i dati più grandi e quelli più piccoli. Se questa differenza è grande, è un segno che i dati sono dispersi, mentre valori piccoli indicano che i dati sono vicini alla media..
Esempio
La gamma per i dati del parador turistico è:
Intervallo = 5−1 = 4
Varianza
-
Varianza per dati non raggruppati
Per trovare la varianza sDue È necessario prima conoscere la media aritmetica, quindi viene calcolata la differenza al quadrato tra ciascun dato e la media, tutte sommate e divise per il numero totale di osservazioni. Queste differenze sono note come deviazioni.

La varianza, che è sempre positiva (o zero), indica quanto sono lontane le osservazioni dalla media: se la varianza è alta, i valori sono più dispersi rispetto a quando la varianza è piccola.
Esempio
La varianza per i dati dell'ostello turistico è:
1; 1; Due; Due; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; Due; Due; 3; 4; 1

-
Varianza per dati raggruppati
Per trovare la varianza di un insieme di dati raggruppati, sono necessari: i) la media, ii) la frequenza fio quali sono i dati totali in ciascuna classe e iii) xio o valore della classe:

La deviazione standard è la radice quadrata positiva della varianza, quindi ha un vantaggio rispetto alla varianza: arriva nelle stesse unità della variabile in esame e quindi hai un'idea più diretta di quanto sia vicina o lontana la variabile dalla media.
-
Deviazione standard per dati non raggruppati
Viene determinato semplicemente trovando la radice quadrata della varianza per i dati non raggruppati:

La deviazione standard per i dati dall'ostello turistico è:
s = √ (sDue) = √1,95 = 1,40
-
Deviazione standard per dati raggruppati
Viene calcolato trovando la radice quadrata della varianza per i dati raggruppati:

Misurazioni di posizione
Le misure di posizione dividono un insieme ordinato di dati in parti di uguale dimensione. La mediana, oltre ad essere una misura della tendenza centrale, è anche una misura della posizione, poiché divide il tutto in due parti uguali. Ma parti più piccole possono essere ottenute con quartili, decili e percentili.
Quartili
I quartili dividono l'insieme in quattro parti uguali, ciascuna contenente il 25% dei dati. Sono indicati come Q1, QDue e Q3 e la mediana è il quartile QDue. In questo modo, il 25% dei dati è al di sotto del quartile Q.1, 50% al di sotto del quartile QDue o mediana e il 75% al di sotto del quartile Q3.

-
Quartili per dati non raggruppati
I dati vengono ordinati e il totale viene diviso in 4 gruppi con lo stesso numero di dati ciascuno. La posizione del primo quartile si trova da:
Q1 = (n + 1) / 4
Dove n è il totale dei dati. Se il risultato è un numero intero, viene localizzato il dato corrispondente a quella posizione, ma se è decimale il dato corrispondente alla parte intera viene mediato con il successivo, oppure per maggiore precisione viene interpolato linearmente tra detti dati.
Esempio
La posizione del primo quartile Q1 per i dati del parador turistico è:
Q1 = (n + 1) / 4 = (20 + 1) / 4 = 5,25
Questa è la posizione del quartile 1 e poiché il risultato è decimale, i dati X vengono cercati5 e X6, che sono rispettivamente X5 = 1 e X6 = 1 e vengono calcolati in media, ottenendo:
Primo quartile = 1
1; 1; 1; 1; 1; 1; 1; Due; Due; Due; Due; 3; 3; 3; 4; 4; 4; 4; 5; 5.
La posizione del secondo quartile QDue è:
QDue = 2 (n + 1) / 4 = 10,5
Qual è la media tra X10 e Xundici e corrisponde alla mediana:
Secondo quartile = Mediana = 2
La posizione del terzo quartile è calcolata da:
Q3 = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75
È anche decimale, quindi X è la mediaquindici e X16:
1; 1; 1; 1; 1; 1; 1; Due; Due; Due; Due; 3; 3; 3; 4; 4; 4; 4; 5; 5.
Ma poiché entrambi valgono 4:
Terzo quartile = 4
La formula generale per la posizione dei quartili nei dati non raggruppati è:
QK = k (n + 1) / 4
Con k = 1,2,3.
-
Quartili per dati raggruppati
Sono calcolati in modo simile alla mediana:

La spiegazione dei simboli è:
-BQ: limite inferiore dell'intervallo contenente il quartile
-c: larghezza di quell'intervallo
-Fche cosa: numero di osservazioni contenute nell'intervallo quartile.
-n: dati totali.
-FBQ: numero di dati prima dell'intervallo contenente il quartile.
Decili e percentili
I decili e i percentili dividono il set di dati rispettivamente in 10 parti uguali e 100 parti uguali e il loro calcolo viene eseguito in modo simile a quello dei quartili.
-
Decili e percentili per dati non raggruppati
Le formule vengono utilizzate rispettivamente:
DK = k (n + 1) / 10
Con k = 1,2,3… 9.
Decile D5 deve essere uguale alla mediana.
PK = k (n + 1) / 100
Con k = 1,2,3… 99.
Il P percentilecinquanta deve essere uguale alla mediana.
Esempio
Nell'esempio dell'ostello turistico, la posizione del D3 è:
D3 = 3 (20 + 1) / 10 = 6,3
Poiché è un numero decimale, viene calcolata la media di X.6 e X7, entrambi uguali a 1:
1; 1; 1; 1; 1; 1; 1; Due; Due; Due; Due; 3; 3; 3; 4; 4; 4; 4; 5; 5
Significa che 3 decimi dei dati sono inferiori a X7 = 1 e i restanti sopra.
-
Decili e percentili per dati raggruppati
Le formule sono analoghe a quelle per i quartili. D è usato per denotare decili e P per percentili, e i simboli sono interpretati in modo simile:

La regola empirica
Quando i dati sono distribuiti simmetricamente e la distribuzione è unimodale, viene chiamata una regola regola empirica o regola 68-95-99, che li raggruppa nei seguenti intervalli:
- Il 68% dei dati rientra nell'intervallo:

- Il 95% dei dati rientra nell'intervallo:

- Il 99% dei dati rientra nell'intervallo:

Esempio
In quale intervallo è il 95% dei dati dal parador turistico?
Sono nell'intervallo: [2.5−1.40; 2,5 + 1,40] = [1,1; 3.9].
Riferimenti
- Berenson, M. 1985. Statistiche per la gestione e l'economia. Interamericana S.A.
- Devore, J. 2012. Probabilità e statistica per l'ingegneria e la scienza. 8 °. Edizione. Cengage.
- Levin, R. 1988. Statistics for Administrators. 2 °. Edizione. Prentice Hall.
- Spiegel, M. 2009. Statistiche. Serie Schaum. 4 ° Edizione. Mcgraw hill.
- Walpole, R. 2007. Probabilità e statistica per l'ingegneria e le scienze. Pearson.

Nessun utente ha ancora commentato questo articolo.