
Caratteristiche della linea perpendicolare, esempi, esercizi
UN linea perpendicolare È uno che forma un angolo di 90 ° rispetto a un'altra linea, curva o superficie. Notare che quando due linee sono perpendicolari e sono sullo stesso piano, quando si intersecano formano quattro angoli identici, ciascuno di 90º.
Se uno degli angoli non è di 90º, le linee si dice che siano oblique. Le linee perpendicolari sono comuni nel design, nell'architettura e nella costruzione, ad esempio la rete di tubi nell'immagine seguente.

L'orientamento delle linee perpendicolari può essere diverso, come quelli mostrati di seguito:
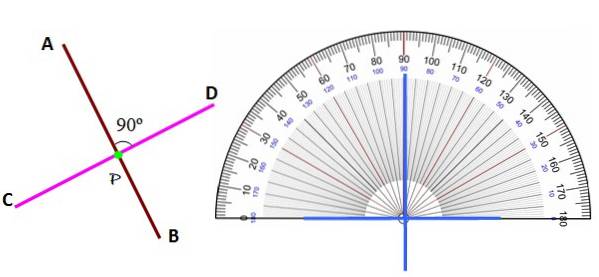
Indipendentemente dalla posizione, le linee perpendicolari tra loro vengono riconosciute identificando l'angolo tra loro di 90 °, con l'aiuto del goniometro.
Si noti che a differenza delle linee parallele nel piano, che non si intersecano mai, le linee perpendicolari lo fanno sempre in un punto P, chiamato piede di una delle righe sull'altra. Quindi sono anche due linee perpendicolari blotters.
Ogni linea ha infinite perpendicolari ad essa, poiché semplicemente spostando il segmento AB a sinistra oa destra sopra il segmento CD, avremo nuove perpendicolari con un altro piede.
Tuttavia, viene chiamata la perpendicolare che passa proprio attraverso il punto medio di un segmento bisettrice di detto segmento.
Indice articolo
- 1 Esempi di linee perpendicolari
- 1.1 Altri esempi di rette perpendicolari
- 2 esercizi
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Esempi di rette perpendicolari
Le linee perpendicolari sono comuni nel paesaggio urbano. Nell'immagine seguente (figura 3), sono state evidenziate solo alcune delle tante linee perpendicolari che possono essere viste nella semplice facciata di questo edificio e dei suoi elementi come porte, condotti, gradini e altro:

La cosa buona è che tre linee perpendicolari l'una all'altra ci aiutano a stabilire la posizione di punti e oggetti nello spazio. Sono gli assi delle coordinate identificati come Asse X., Asse y Y asse z, ben visibile nell'angolo di una stanza rettangolare come quella sottostante:
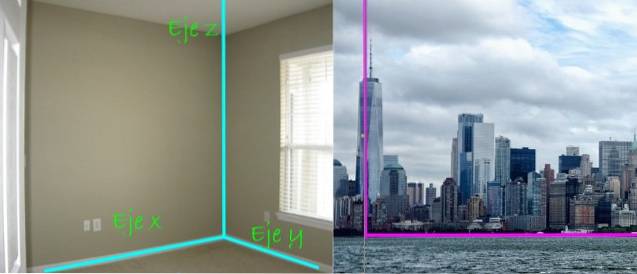
Nella vista panoramica della città, a destra, si nota anche la perpendicolarità tra il grattacielo e il terreno. Il primo, diremmo, si trova lungo il asse z, mentre il suolo è un aereo, che in questo caso è l'aereo xy.
Se il suolo costituisce l'aereo xy, il grattacielo è anche perpendicolare a qualsiasi viale o strada, il che ne garantisce la stabilità, poiché una struttura in pendenza è instabile.
E nelle strade, ovunque ci siano angoli rettangolari, ci sono linee perpendicolari. Molti viali e strade hanno una disposizione perpendicolare, purché il terreno e le caratteristiche geografiche lo consentano..
Per esprimere brevemente la perpendicolarità tra linee, segmenti o vettori, viene utilizzato il simbolo ⊥. Ad esempio, se la riga L1 è perpendicolare alla linea LDue, abbiamo scritto:
L1 ⊥ LDue
Altri esempi di linee perpendicolari
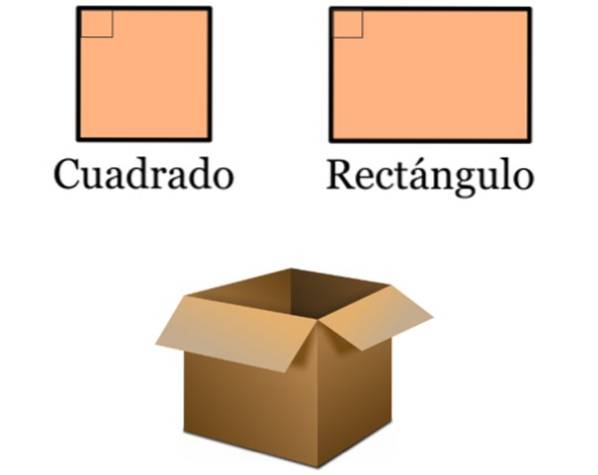
- Nel disegno le linee perpendicolari sono molto presenti, poiché molti oggetti comuni sono basati su quadrati e rettangoli. Questi quadrilateri sono caratterizzati dall'avere angoli interni di 90º, perché i loro lati sono paralleli a due a due:
- I campi in cui si praticano diversi sport sono delimitati da numerose piazze e rettangoli. Questi a loro volta contengono linee perpendicolari.
- Due dei segmenti che compongono un triangolo rettangolo sono perpendicolari tra loro. Questi sono chiamati gambe, mentre viene chiamata la riga rimanente ipotenusa.
- Le linee del vettore del campo elettrico sono perpendicolari alla superficie di un conduttore in equilibrio elettrostatico.
- Per un conduttore carico, le linee e le superfici equipotenziali sono sempre perpendicolari a quelle del campo elettrico.
- Nei sistemi di tubazioni o condotti utilizzati per trasportare diversi tipi di fluidi, come il gas mostrato nella Figura 1, i gomiti ad angolo retto sono comuni. Pertanto formano linee perpendicolari, come nel caso di un locale caldaia:

Formazione
- Esercizio 1
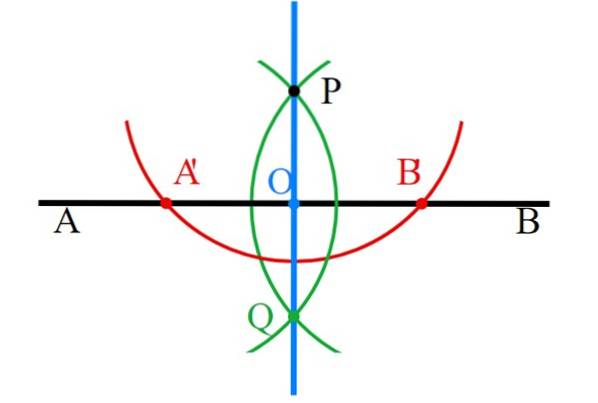
Disegna due linee perpendicolari usando un righello e un compasso.
Soluzione
È molto semplice da fare, seguendo questi passaggi:
-Viene tracciata la prima riga, chiamata AB (nera).
-Al di sopra (o al di sotto se si preferisce) AB segna il punto P, attraverso il quale passerà la perpendicolare. Se P è appena sopra (o sotto) la metà di AB, quella perpendicolare è la bisettrice del segmento AB.
-Con il compasso centrato su P, disegna un cerchio che taglia AB in due punti, chiamati A 'e B' (rosso).
-La bussola viene aperta in A'P, è centrata su A 'e viene disegnato un cerchio che passa per P (verde).
-Ripetere il passaggio precedente, ma ora aprendo la misura la lunghezza del segmento B'P (verde). Entrambi gli archi di circonferenza si intersecano nel punto Q sotto P e ovviamente in quest'ultimo.
-I punti P e Q sono uniti con il righello e la linea perpendicolare (blu) è pronta.
-Infine, tutte le costruzioni ausiliarie devono essere accuratamente cancellate, lasciando solo quelle perpendicolari..
- Esercizio 2
Due linee L1 e ioDue sono perpendicolari se le rispettive pendenze m1 e mDue incontrare questa relazione:
m1 = -1 / mDue
Data la retta y = 5x - 2, trova una retta perpendicolare ad essa e che passi per il punto (-1, 3).
Soluzione
-Per prima cosa, trova la pendenza della linea perpendicolare m⊥, come indicato nella dichiarazione. La pendenza della linea originale è m = 5, il coefficiente che accompagna “x”. Poi:
m⊥= -1/5
-Quindi viene costruita l'equazione della linea perpendicolare e⊥, sostituendo il valore precedentemente trovato:
Y⊥= -1 / 5x + b
-Successivamente, il valore di b viene determinato, con l'aiuto del punto dato dall'istruzione, (-1,3), poiché la retta perpendicolare deve attraversarlo:
y = 3
x = -1
Sostituzione:
3 = -1/5 (-1) + b
Risolvi per il valore di b:
b = 3- (1/5) = 14/5
-Infine viene costruita l'equazione definitiva:
Y⊥= -1 / 5x + 14/5
Riferimenti
- Baldor, A. 2004. Geometria del piano e dello spazio. Pubblicazioni culturali.
- Clemens, S. 2001. Geometria con applicazioni e risoluzione di problemi. Addison Wesley.
- La matematica è divertente. Linee perpendicolari. Estratto da: mathisfun.com.
- Monterey Institute. Linee perpendicolari. Estratto da: montereyinstitute.org.
- Wikipedia. Linee perpendicolari. Estratto da: es.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.