
Le leggi di Keplero spiegazione, esercizi, esperimenti
Il Le leggi di Keplero sul moto planetario furono formulate dall'astronomo tedesco Johannes Kepler (1571-1630). Keplero li ha dedotti basandosi sul lavoro del suo maestro l'astronomo danese Tycho Brahe (1546-1601).
Brahe ha accuratamente compilato i dati sui movimenti planetari per più di 20 anni, con sorprendente precisione e accuratezza, considerando che il telescopio non era ancora stato inventato all'epoca. La validità dei tuoi dati è ancora valida oggi.

Indice articolo
- 1 Le 3 leggi di Keplero
- 2 Legge di gravitazione universale e terza legge di Keplero
- 3 esercizi
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 4 esperimento
- 4.1 Materiali
- 4.2 Procedura
- 5 Riferimenti
Le 3 leggi di Keplero
Le leggi di Keplero affermano:
-Prima legge: tutti i pianeti descrivono orbite ellittiche con il Sole in uno dei fuochi.
-Seconda legge o legge delle pari aree: una linea diretta dal Sole a qualsiasi pianeta (raggio focale), percorre aree uguali in tempi uguali.
-Terza legge: il quadrato del tempo impiegato da un pianeta per orbitare attorno al Sole è proporzionale al cubo della sua distanza media dal Sole.
Essere T ha detto il tempo, ha chiamato periodo orbitale, Y r la distanza media, quindi:
TDue è proporzionale a r3
T = k r3
Ciò significa che il quoziente TDue/ r3 è lo stesso per tutti i pianeti, il che rende possibile calcolare il raggio orbitale, se il periodo orbitale è noto.
quando T è espresso in anni e r in unità astronomiche AU *, la costante di proporzionalità è k = 1:
TDue= r3
* Un'unità astronomica equivale a 150 milioni di chilometri, che è la distanza media tra la Terra e il Sole. Il periodo orbitale della Terra è di 1 anno.
Legge di gravitazione universale e terza legge di Keplero
La legge universale di gravitazione afferma che l'ampiezza della forza gravitazionale di attrazione tra due oggetti di massa M Y m rispettivamente, i cui centri sono separati da una distanza r, è dato da:
F = G mM / rDue
G è la costante universale di gravitazione e il suo valore è G = 6,674 x 10 -undici N.mDue/ kgDue .
Ora, le orbite dei pianeti sono ellittiche con un'eccentricità molto piccola.
Ciò significa che l'orbita non è molto lontana da una circonferenza, tranne in alcuni casi come il pianeta nano Plutone. Se approssimiamo le orbite alla forma circolare, l'accelerazione del moto del pianeta è:
perc = vDue/ r
dato che F = ma, avere:
G mM / rDue = m.vDue/ r
Qui v è la velocità lineare del pianeta attorno al Sole, assunta statica e di massa M, mentre quella del pianeta lo è m. Poi:

Questo spiega che i pianeti più lontani dal Sole hanno una velocità orbitale inferiore, poiché questa dipende da 1 / √r.
Poiché la distanza percorsa dal pianeta è approssimativamente la lunghezza della circonferenza: L = 2πr e impiega un tempo pari a T, periodo orbitale, otteniamo:
v = 2πr / T
L'equalizzazione di entrambe le espressioni per v fornisce un'espressione valida per TDue, il quadrato del periodo orbitale:

E questa è precisamente la terza legge di Keplero, poiché in questa espressione la parentesi 4πDue / GM è costante, quindi TDue è proporzionale alla distanza r a cubetti.
L'equazione definitiva per il periodo orbitale si ottiene prendendo la radice quadrata:

Quanto vale la massa del Sole? È possibile scoprirlo con questa equazione. Sappiamo che il periodo orbitale della Terra è di un anno e il raggio orbitale è di 1 UA, equivalente a 150 milioni di chilometri, quindi abbiamo tutti i dati necessari.
Nella nostra precedente equazione, risolviamo per M, non senza prima convertire tutti i valori nel Sistema internazionale di unità SI:
1 anno = 3,16 x 107 secondi.
1 UA = 150 milioni di km = 1,5 x10undici m.

Formazione
Sebbene Keplero avesse in mente solo i pianeti quando derivò le sue famose leggi, queste sono valide anche per il movimento dei satelliti e di altri corpi nel sistema solare, come vedremo più avanti..
- Esercizio 1
Sapendo che l'orbita di Giove è 5,19 volte quella della Terra, trova il periodo orbitale di Giove.
Soluzione
Secondo la definizione di Unità Astronomica, Giove è distante dal Sole 5,19 UA, quindi, secondo la terza legge di Keplero:
TDue= r3= (5,19)3 anni
Perciò T = (5,19)3/2 anni = 11,8 anni
- Esercizio 2
La cometa Halley visita il Sole ogni 75,3 anni. Trova:
a) Il semiasse maggiore della sua orbita.
b) La misura dell'afelio, se il perielio misura 0,568 UA.
Soluzione
La cometa Halley visita il Sole ogni 75,3 anni. Trova:
a) Il semiasse maggiore della sua orbita.
b) La misura dell'afelio, se il perielio misura 0,568 UA.
Soluzione a
Quando un pianeta o qualsiasi altra stella si trova nel punto più vicino al Sole, si dice che si trovi nel perielio, e quando è più lontano, dentro afelio. Nel caso speciale di un'orbita circolare, r nella terza legge di Keplero è il raggio dell'orbita.
Tuttavia, nell'orbita ellittica il corpo celeste è più o meno lontano dal Sole, il semiasse maggiore "a" è la media tra afelio e perielio:

Pertanto, sostituiamo r con a nella terza legge di Keplero, che risulta per Halley in:
TDue= a3→ a = (T)2/3 → a = (75,3) 2/3 UA = 17.832 UA
Soluzione b
a = ½ (Perielio + Afelio)
17,832 = ½ (0,568+ Aphelion) → Aphelion = 2 x 17,832 - 0,568 UA = 35,10 UA.
Sperimentare
L'analisi del moto dei pianeti richiede settimane, mesi e persino anni di attenta osservazione e registrazione. Ma in laboratorio può essere condotto un esperimento su scala molto semplice per dimostrare che vale la legge di Keplero delle aree uguali..
Per questo, è necessario un sistema fisico in cui la forza che governa il movimento sia centrale, condizione sufficiente perché la legge delle aree sia soddisfatta. Un tale sistema è costituito da una massa legata a una lunga fune, con l'altra estremità del filo fissata a un supporto..
La massa viene spostata di un piccolo angolo dalla sua posizione di equilibrio e le viene dato un leggero impulso, in modo che esegua un movimento ovale (quasi ellittico) sul piano orizzontale, come se fosse un pianeta attorno al Sole..
Sulla curva descritta dal pendolo, possiamo dimostrare che percorre aree uguali in tempi uguali, se:
-Consideriamo i raggi del vettore che vanno dal centro di attrazione (punto di equilibrio iniziale) alla posizione della massa.
-E spazziamo tra due istanti consecutivi di uguale durata, in due diverse aree del movimento.
Più lunga è la corda del pendolo e minore è l'angolo dalla verticale, la forza di ripristino netta sarà più orizzontale e la simulazione assomiglia al caso di movimento con forza centrale su un piano.
Quindi l'ovale descritto si avvicina a un'ellisse, come quella percorsa dai pianeti.
Materiali
-Filo inestensibile
-1 impasto o palla metallica verniciata di bianco che funge da pendolo
-Righello
-Trasportatore
-Fotocamera fotografica con disco strobo automatico
-Parentesi
-Due sorgenti luminose
-Un foglio di carta o cartone nero
Processi
L'assemblaggio della figura è necessario per scattare foto di più lampi del pendolo mentre segue il suo percorso. Per fare questo devi mettere la fotocamera appena sopra il pendolo e il disco strobo automatico davanti all'obiettivo.
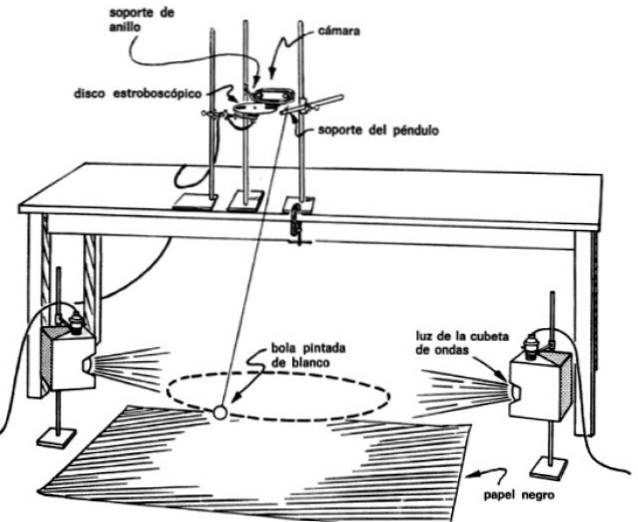
In questo modo si ottengono immagini ad intervalli di tempo regolari del pendolo, ad esempio ogni 0,1 o ogni 0,2 secondi, il che permette di conoscere il tempo impiegato per spostarsi da un punto all'altro..
Devi anche illuminare adeguatamente la massa del pendolo, mettendo le luci su entrambi i lati. La lenticchia va dipinta di bianco per migliorare il contrasto sullo sfondo, che consiste in una carta nera stesa a terra.
Ora devi controllare che il pendolo percorra aree uguali in tempi uguali. Per fare ciò si sceglie un intervallo di tempo e si segnano sulla carta i punti occupati dal pendolo in detto intervallo..
Nell'immagine viene tracciata una linea dal centro dell'ovale a questi punti e così avremo la prima delle aree spazzate dal pendolo, che è approssimativamente un settore ellittico come quello mostrato sotto:
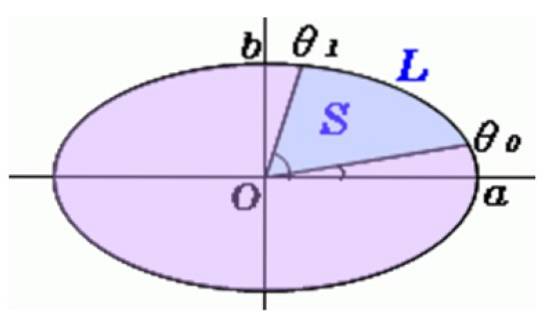
Calcolo dell'area della sezione ellittica
Gli angoli vengono misurati con il goniometro θo Y θ1, e questa formula è usata per trovare S, l'area del settore ellittico:
S = F (θ1) - F (θo)
Con F (θ) dato da:

Notare che per Y b sono rispettivamente il semiasse maggiore e minore. Il lettore deve solo preoccuparsi di misurare attentamente i semiassi e gli angoli, poiché ci sono calcolatori online per valutare facilmente questa espressione..
Tuttavia, se insisti a fare il calcolo a mano, ricorda che l'angolo θ è misurato in gradi, ma quando inserisci i dati nella calcolatrice, i valori devono essere espressi in radianti.
Quindi devi segnare un'altra coppia di punti in cui il pendolo ha invertito lo stesso intervallo di tempo, e disegnare l'area corrispondente, calcolandone il valore con la stessa procedura.
Verifica del diritto delle pari aree
Infine, resta da verificare che la legge delle aree sia rispettata, cioè che le aree uguali siano spazzate in tempi uguali.
I risultati si discostano un po 'da quanto previsto? Va sempre tenuto presente che tutte le misurazioni sono accompagnate dal rispettivo errore sperimentale.
Riferimenti
- Calcolatrice online Keisan. Area di un calcolatore di settore ellittico. Estratto da: keisan.casio.com.
- Openstax. Legge di Keplero del moto planetario. Recupero da: openstax.org.
- PSSC. Fisica di laboratorio. Reverté editoriale. Estratto da: books.google.co.
- Palen, S. 2002. Astronomia. Serie Schaum. Mcgraw hill.
- Pérez R. Sistema semplice con forza centrale. Estratto da: francesphysics.blogspot.com
- Stern, le tre leggi del moto planetario di D. Keplero. Estratto da: phy6.org.



Nessun utente ha ancora commentato questo articolo.