
Funzione iniettiva cos'è, a cosa serve ed esempi

UN funzione iniettiva è qualsiasi relazione di elementi del dominio con un singolo elemento del codominio. Conosciuta anche come funzione uno per uno ( undici ), fanno parte della classificazione delle funzioni rispetto al modo in cui i loro elementi sono correlati.
Un elemento del codominio può essere solo l'immagine di un singolo elemento del dominio, in questo modo i valori della variabile dipendente non possono essere ripetuti.
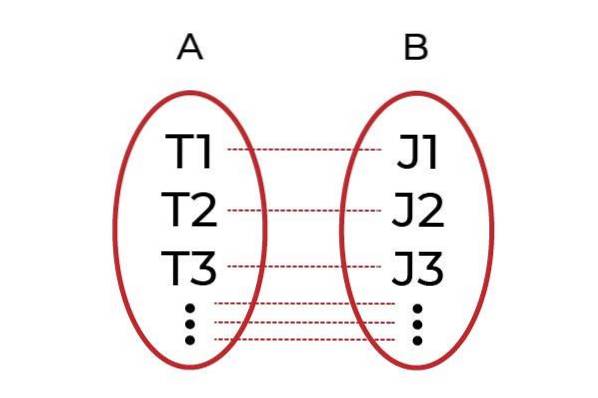
Un chiaro esempio potrebbe essere il raggruppamento di uomini con lavori nel gruppo A e nel gruppo B tutti i capi. La funzione F Sarà quello che assocerà ogni lavoratore al proprio capo. Se ogni lavoratore è associato a un capo diverso tramite F, poi F sarà un funzione iniettiva.
Considerare iniettiva per una funzione deve essere soddisfatto quanto segue:
∀ x1 ≠ xDue ⇒ F (x1 ) ≠ F (xDue )
Questo è il modo algebrico di dire Per tutti x1 diverso da xDue hai una F (x1 ) diverso da F (xDue ).
Indice articolo
- 1 A cosa servono le funzioni di iniezione?
- 1.1 Condizionamento funzionale
- 2 Esempi di funzioni di iniezione con esercizi risolti
- 2.1 Esempio 1
- 2.2 Esempio 2
- 2.3 Esempio 3
- 2.4 Esempio 4
- 2.5 Esempio 5
- 2.6 Esempio 6
- 2.7 Esempio 7
- 3 Esercizi proposti per classe / casa
- 4 Riferimenti
A cosa servono le funzioni iniettive?
L'iniettività è una proprietà delle funzioni continue, poiché garantiscono l'assegnazione di immagini per ogni elemento del dominio, aspetto essenziale nella continuità di una funzione..
Quando si traccia una linea parallela all'asse X sul grafico di una funzione iniettiva, dovresti toccare il grafico solo in un singolo punto, indipendentemente dall'altezza o dall'ampiezza del Y la linea è tracciata. Questo è il modo grafico per testare l'iniettività di una funzione.
Un altro modo per verificare se una funzione è iniettiva, sta risolvendo per la variabile indipendente X in termini di variabile dipendente Y. Quindi è necessario verificare se il dominio di questa nuova espressione contiene i numeri reali, contemporaneamente a ciascun valore di Y c'è un unico valore di X.
Le funzioni o le relazioni di ordine obbediscono, tra l'altro, alla notazione F: DF→CF
Cosa viene letto F che va da DF fino a CF
Dove la funzione F mettere in relazione le serie Dominio Y Codominio. Conosciuto anche come set di partenza e set di arrivo.
Il dominio DF contiene i valori consentiti per la variabile indipendente. Il codominio CF È composto da tutti i valori disponibili per la variabile dipendente. Gli elementi di CF relativo a DF sono conosciuti come Gamma di funzioni (RF ).
Condizionamento funzionale
A volte una funzione che non è iniettiva può essere soggetta a determinate condizioni. Queste nuove condizioni possono renderlo un file funzione iniettiva. Sono validi tutti i tipi di modifiche al dominio e al codominio della funzione, dove l'obiettivo è soddisfare le proprietà di iniettività nella relazione corrispondente.
Esempi di funzioni di iniezione con esercizi risolti
Esempio 1
Lascia che la funzione F: R → R definito dalla linea F (x) = 2x - 3
A: [Tutti i numeri reali]
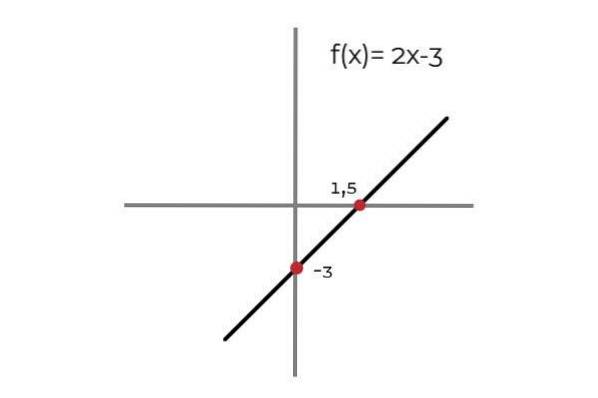
Si osserva che per ogni valore del dominio c'è un'immagine nel codominio. Questa immagine è unica, il che rende F una funzione iniettiva. Questo vale per tutte le funzioni lineari (funzioni il cui massimo grado di variabile è uno).
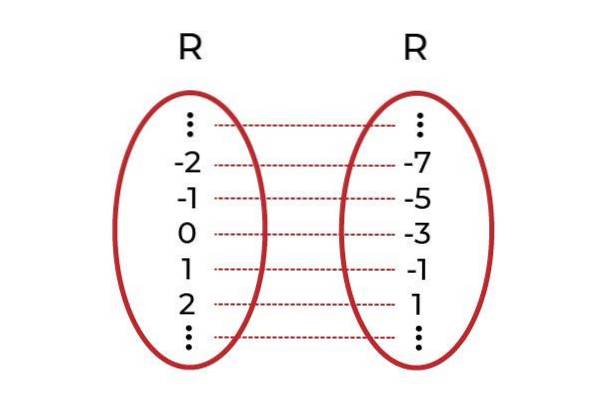
Esempio 2
Lascia che la funzione F: R → R definito da F (x) = xDue +1
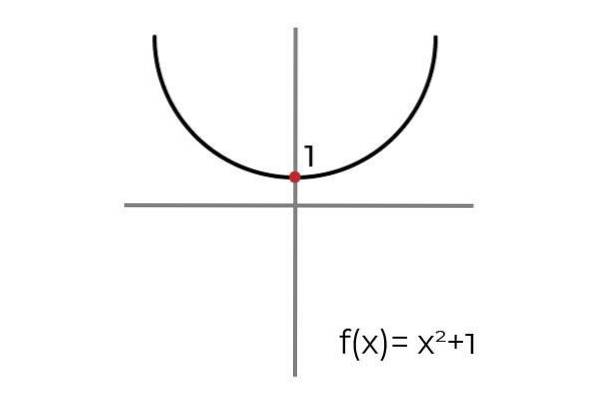
Quando si traccia una linea orizzontale, si osserva che il grafico si trova in più di un'occasione. Per questo motivo la funzione F non è iniettiva fintanto che è definita R → R
Procediamo a condizionare il dominio della funzione:
F: R+ O 0 → R
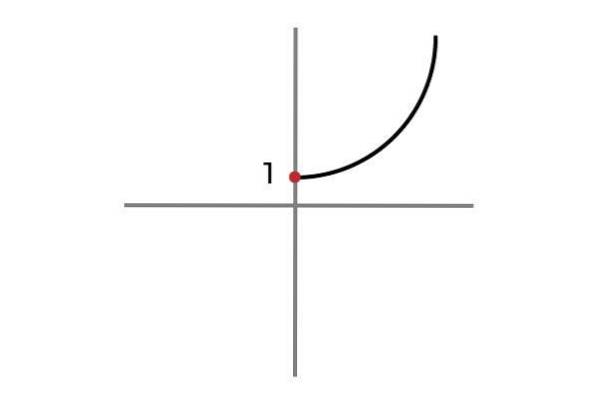
Ora la variabile indipendente non assume valori negativi, in questo modo si evita la ripetizione dei risultati e la funzione F: R+ O 0 → R definito da F (x) = xDue + 1 è iniettiva.
Un'altra soluzione omologa sarebbe quella di limitare il dominio a sinistra, cioè restringere la funzione a prendere solo valori negativi e zero.
Procediamo a condizionare il dominio della funzione
F: R- O 0 → R
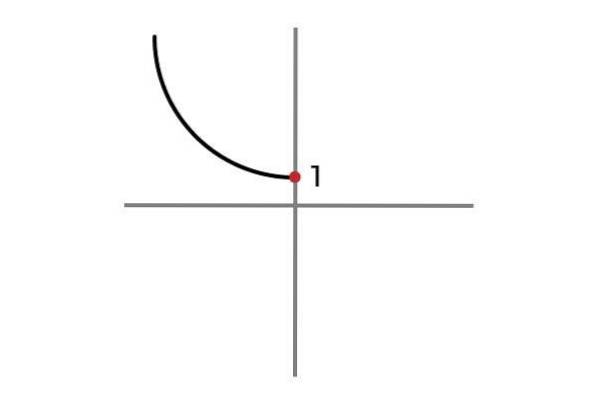
Ora la variabile indipendente non assume valori negativi, in questo modo si evita la ripetizione dei risultati e la funzione F: R- O 0 → R definito da F (x) = xDue + 1 è iniettiva.
Le funzioni trigonometriche hanno comportamenti simili alle onde, dove è molto comune trovare ripetizioni di valori nella variabile dipendente. Attraverso un condizionamento specifico, basato sulla conoscenza preliminare di queste funzioni, possiamo restringere il dominio per soddisfare le condizioni di iniettività.
Esempio 3
Lascia la funzione F: [ -π / 2, π / 2 ] → R definito da F (x) = Cos (x)
Nell'intervallo [ -π / 2 → π / 2 ] la funzione coseno varia i suoi risultati tra zero e uno.
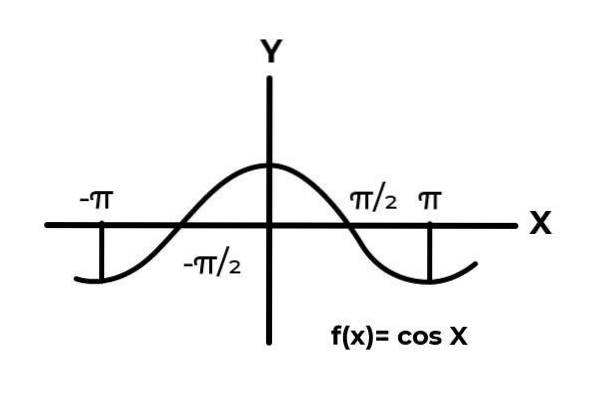
Come si può vedere dal grafico. Inizia da zero x = -π / 2 quindi raggiungendo un massimo a zero. È dopo x = 0 che i valori iniziano a ripetersi, fino a quando non tornano a zero x = π / 2. In questo modo si sa che F (x) = Cos (x) non è iniettivo per l'intervallo [ -π / 2, π / 2 ] .
Quando si studia il grafico della funzione F (x) = Cos (x) si osservano intervalli in cui il comportamento della curva si adatta ai criteri di iniettività. Come ad esempio l'intervallo
[0 , π ]
Dove la funzione varia i risultati da 1 a -1, senza ripetere alcun valore nella variabile dipendente.
In questo modo la funzione function F: [0 , π ] → R definito da F (x) = Cos (x). È iniettiva
Esistono funzioni non lineari in cui si verificano casi simili. Per le espressioni di tipo razionale, dove il denominatore contiene almeno una variabile, esistono delle restrizioni che impediscono l'iniettività della relazione.
Esempio 4
Lascia la funzione F: R → R definito da F (x) = 10 / x
La funzione è definita per tutti i numeri reali tranne 0 chi ha un'indeterminatezza (non può essere diviso per zero).
Quando ci si avvicina allo zero da sinistra, la variabile dipendente assume valori negativi molto grandi e, immediatamente dopo lo zero, i valori della variabile dipendente assumono grandi cifre positive.
Questa interruzione causa l'espressione F: R → R definito da F (x) = 10 / x
Non essere iniettivo.
Come visto negli esempi precedenti, l'esclusione di valori nel dominio serve a "riparare" queste indeterminatezze. Si procede ad escludere zero dal dominio, lasciando i set di partenza e arrivo definiti come segue:
R - 0 → R
Dove R - 0 simboleggia i reali ad eccezione di un insieme il cui unico elemento è zero.
In questo modo l'espressione F: R - 0 → R definito da F (x) = 10 / x è iniettiva.
Esempio 5
Lascia la funzione F: [0 , π ] → R definito da F (x) = Sen (x)
Nell'intervallo [0 , π ] la funzione seno varia i suoi risultati tra zero e uno.
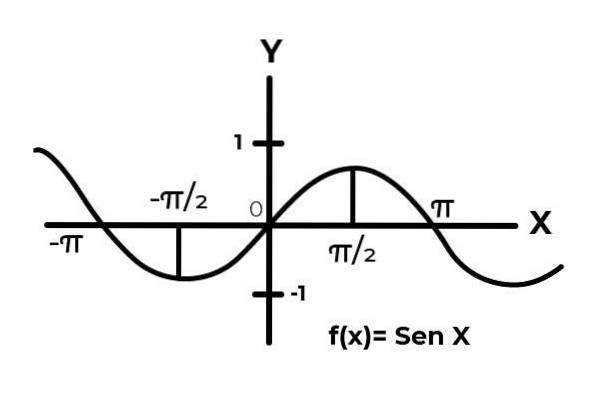
Come si può vedere dal grafico. Inizia da zero x = 0 quindi raggiungendo un massimo in x = π / 2. È dopo x = π / 2 che i valori iniziano a ripetersi, fino a tornare a zero x = π. In questo modo si sa che F (x) = Sen (x) non è iniettiva per l'intervallo [0 , π ] .
Quando si studia il grafico della funzione F (x) = Sen (x) si osservano intervalli in cui il comportamento della curva si adatta ai criteri di iniettività. Come ad esempio l'intervallo [ π / 2,3π / 2 ]
Dove la funzione varia i risultati da 1 a -1, senza ripetere alcun valore nella variabile dipendente.
In questo modo la funzione F: [ π / 2,3π / 2 ] → R definito da F (x) = Sen (x). È iniettiva
Esempio 6
Controlla se la funzione F: [0, ∞) → R definito da F (x) = 3xDue è iniettiva.
Questa volta il dominio dell'espressione è già limitato. Si osserva inoltre che i valori della variabile dipendente non si ripetono in questo intervallo.
Pertanto, si può concludere che F: [0, ∞) → R definito da F (x) = 3xDue è iniettiva
Esempio 7
Identifica quale delle seguenti funzioni è
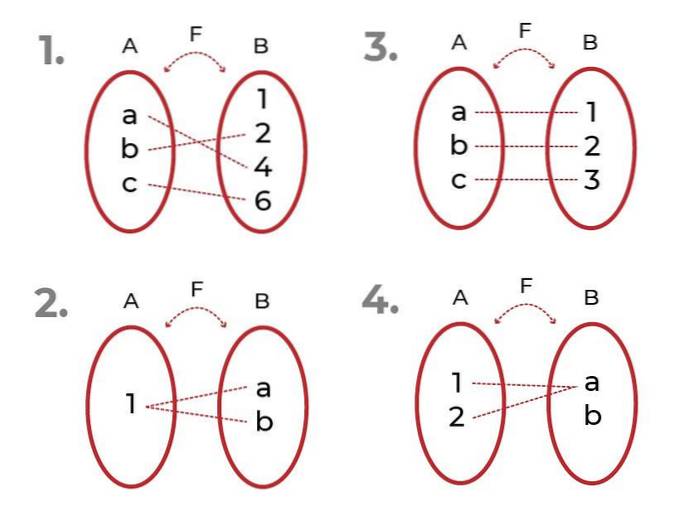
- È iniettiva. Gli elementi associati del codominio sono unici per ogni valore della variabile indipendente.
- Non è iniettabile. Ci sono elementi del codominio associati a più di un elemento dell'insieme di partenza.
- È iniettiva
- Non è iniettabile
Esercizi proposti per classe / casa
Controlla se le seguenti funzioni sono iniettive:
F: [0, ∞) → R definito da F (x) = (x + 3)Due
F: [ π / 2,3π / 2 ] → R definito da F (x) = Tan (x)
F: [ -π,π ] → R definito da F (x) = Cos (x + 1)
F: R → R definito dalla linea F (x) = 7x + 2
Riferimenti
- Introduzione alla logica e al pensiero critico. Merrilee H. Salmon. Università di Pittsburgh
- Problemi nell'analisi matematica. Piotr Biler, Alfred Witkowski. Università di Wroclaw. Polonia.
- Elementi di analisi astratta. Mícheál O'Searcoid PhD. Dipartimento di matematica. College universitario di Dublino, Beldfield, Dublino 4.
- Introduzione alla logica e alla metodologia delle scienze deduttive. Alfred Tarski, New York Oxford. La stampa dell'università di Oxford.
- Principi di analisi matematica. Enrique Linés Escardó. Editoriale Reverté S. A 1991. Barcellona Spagna.



Nessun utente ha ancora commentato questo articolo.