
Funzione biettiva che cos'è, come si fa, esempi, esercizi

UN funzione biiettiva è quella che soddisfa la doppia condizione dell'essere iniettiva e suriettiva. Cioè, tutti gli elementi del dominio hanno un'unica immagine nel codominio, ea sua volta il codominio è uguale al rango della funzione ( RF ).
Si realizza considerando una relazione uno-a-uno tra gli elementi del dominio e del codominio. Un semplice esempio è la funzione F: R → R definito dalla linea F (x) = x
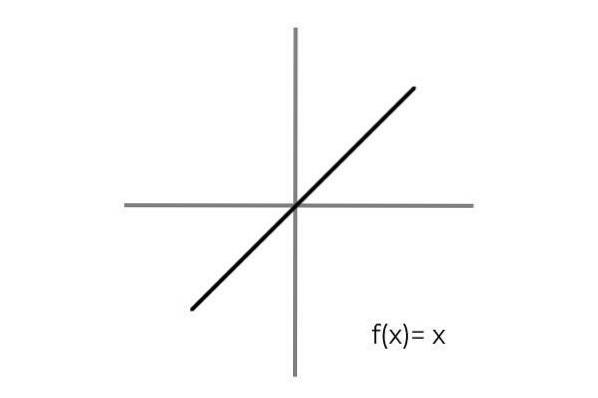
Si osserva che per ogni valore del dominio o insieme di partenza (entrambi i termini si applicano allo stesso modo) c'è una singola immagine nel codominio o insieme di arrivo. Inoltre, non vi è alcun elemento del codominio che non sia un'immagine.
Così F: R → R definito dalla linea F (x) = x è biettivo
Indice articolo
- 1 Come si esegue una funzione biiettiva?
- 1.1 Iniettività di una funzione
- 1.2 Surjectivity di una funzione
- 1.3 Condizionamento funzionale
- 2 Esempi: esercizi risolti
- 2.1 Esercizio 1
- 2.2 Esercizio 2
- 2.3 Esercizio 3
- 2.4 Esercizio 4
- 3 Esercizi proposti
- 4 Riferimenti
Come si esegue una funzione biiettiva?
Per rispondere a questa domanda è necessario essere chiari sui concetti a cui si fa riferimento Iniettività Y Surjectivity di una funzione, oltre ai criteri per condizionare le funzioni al fine di adattarle alle esigenze.
Iniettività di una funzione
Una funzione è iniettiva quando ciascuno degli elementi del suo dominio è correlato a un singolo elemento del codominio. Un elemento del codominio può essere solo l'immagine di un singolo elemento del dominio, in questo modo i valori della variabile dipendente non possono essere ripetuti.
Considerare iniettiva per una funzione deve essere soddisfatto quanto segue:
∀ x1 ≠ xDue ⇒ F (x1 ) ≠ F (xDue )
Surjectivity di una funzione
Una funzione è classificata come surjective, se ogni elemento del suo codominio è un'immagine di almeno un elemento del dominio.
Considerare surjective per una funzione deve essere soddisfatto quanto segue:
Essere F: DF → CF
∀ b ℮ CF E a ℮ DF / F (a) = b
Questo è il modo algebrico per stabilirlo per ogni "b" che appartiene a CF c'è una "a" che appartiene a DF tale che la funzione valutata in "a" sia uguale a "b".
Condizionamento funzionale
A volte una funzione che non lo è biettivo, può essere soggetto a determinate condizioni. Queste nuove condizioni possono renderlo un file funzione biiettiva. Sono validi tutti i tipi di modifiche al dominio e al codominio della funzione, laddove l'obiettivo è soddisfare le proprietà di iniettività e suriettività nella relazione corrispondente..
Esempi: esercizi risolti
Esercizio 1
Lascia che la funzione F: R → R definito dalla linea F (x) = 5x +1
A: [Tutti i numeri reali]
Si osserva che per ogni valore del dominio c'è un'immagine nel codominio. Questa immagine è unica che fa F essere un funzione iniettiva. Allo stesso modo, osserviamo che il codominio della funzione è uguale al suo rango. Così soddisfacendo la condizione di suriettività.
Essendo iniettivi e suriettivi allo stesso tempo possiamo concludere che
F: R → R definito dalla linea F (x) = 5x +1 è un funzione biiettiva.
Questo vale per tutte le funzioni lineari (funzioni il cui massimo grado di variabile è uno).
Esercizio 2
Lascia che la funzione F: R → R definito da F (x) = 3xDue - Due
Quando si traccia una linea orizzontale, si osserva che il grafico si trova in più di un'occasione. Per questo motivo la funzione F non è iniettiva e quindi non lo sarà biettivo fintanto che è definito in R → R
Allo stesso modo, ci sono valori del codominio che non sono immagini di alcun elemento del dominio. Per questo la funzione non è suriettiva, che merita anche di condizionare il set di arrivo.
Procediamo a condizionare il dominio e il codominio della funzione
F: [0 , ∞] → [ - Due , ∞ ]
Dove si osserva che il nuovo dominio comprende i valori da zero a infinito positivo. Evitare la ripetizione di valori che influiscono sull'iniettività.
Allo stesso modo è stato modificato il codominio, contando da "-2" a infinito positivo, eliminando dal codominio i valori che non corrispondevano a nessun elemento del dominio
In questo modo lo si può garantire F : [0 , ∞] → [ - Due , ∞ ] definito da F (x) = 3xDue - Due
È biettivo
Esercizio 3
Lascia che la funzione F: R → R definito da F (x) = Sen (x)
Nell'intervallo [ -∞ , +∞ ] la funzione seno varia i suoi risultati tra zero e uno.
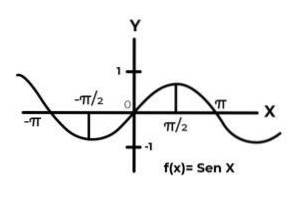
La funzione F non corrisponde ai criteri di iniettività e suriettività, perché i valori della variabile dipendente si ripetono ad ogni intervallo di π. Anche i termini del codominio fuori intervallo [ -undici ] Non sono un'immagine di alcun elemento del dominio.
Quando si studia il grafico della funzione F (x) = Sen (x) vengono osservati intervalli in cui il comportamento della curva soddisfa i criteri di biiettività. Come ad esempio l'intervallo DF = [ π / 2,3π / 2 ] per il dominio. Y CF = [-1, 1] per il codominio.
Dove la funzione varia i risultati da 1 a -1, senza ripetere alcun valore nella variabile dipendente. E allo stesso tempo il codominio è uguale ai valori adottati dall'espressione Sen (x)
In questo modo la funzione F: [ π / 2,3π / 2 ] → [-1, 1] definito da F (x) = Sen (x). È biettivo
Esercizio 4
Indicare le condizioni necessarie per DF e CF. Quindi l'espressione
F (x) = -xDue essere biunivoci.
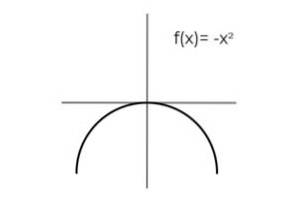
La ripetizione dei risultati si osserva quando la variabile assume valori opposti:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
Il dominio è condizionato, limitandolo al lato destro della linea reale.
DF = [0 , +∞ ]
Allo stesso modo, si osserva che l'intervallo di questa funzione è l'intervallo [ -∞ , 0], che quando agisce come un codominio soddisfa le condizioni della suriettività.
In questo modo possiamo concludere che
L'espressione F: [0 , +∞ ] → [ -∞ , 0] definito da F (x) = -xDue È biettivo
Esercizi proposti
Controlla se le seguenti funzioni sono biiettive:
F: [0 , ∞) → R definito da F (x) = 3 (x + 1)Due +Due
F: [ 3π / 2,5π / 2 ] → R definito da F (x) = 5ctg (x)
F: [ -π,π ] → R definito da F (x) = Cos (x - 3)
F: R → R definito dalla linea F (x) = -5x + 4
Riferimenti
- Introduzione alla logica e al pensiero critico. Merrilee H. Salmon. Università di Pittsburgh
- Problemi nell'analisi matematica. Piotr Biler, Alfred Witkowski. Università di Wroclaw. Polonia.
- Elementi di analisi astratta. Mícheál O'Searcoid PhD. Dipartimento di matematica. College universitario di Dublino, Beldfield, Dublino 4
- Introduzione alla logica e alla metodologia delle scienze deduttive. Alfred Tarski, New York Oxford. La stampa dell'università di Oxford.
- Principi di analisi matematica. Enrique Linés Escardó. Editoriale Reverté S. A 1991. Barcellona Spagna.


Nessun utente ha ancora commentato questo articolo.