
Storia statistica descrittiva, caratteristiche, esempi, concetti
Il Statistiche descrittive è il ramo della Statistica che si occupa di raccogliere e organizzare le informazioni sul comportamento dei sistemi con molti elementi, conosciuti genericamente con il nome di popolazione.
Per fare ciò utilizza tecniche numeriche e grafiche, attraverso le quali presenta le informazioni, senza fare previsioni o inferenze sulla popolazione da cui provengono..

Indice articolo
- 1 Storia
- 1.1 Età antica
- 1.2 Rinascimento
- 1.3 Età moderna
- 2 Caratteristiche della statistica descrittiva
- 3 A cosa servono le statistiche descrittive?
- 3.1 Economia
- 3.2 Fisica e meccanica
- 3.3 Medicina
- 3.4 Nutrizione
- 4 Esempi di statistiche descrittive
- 4.1 Esempio 1
- 4.2 Esempio 2
- 4.3 Esempio 3
- 5 Concetti di base della statistica descrittiva
- 5.1 Popolazione
- 5.2 Campione
- 5.3 Variabile
- 5.4 Misure di tendenza centrale
- 5.5 Misurazioni della dispersione
- 6 Argomenti di interesse
- 7 Riferimenti
Storia
Vecchiaia
La statistica ha le sue origini nella necessità umana di organizzare le informazioni necessarie alla sua sopravvivenza e al suo benessere, nonché di anticipare gli eventi che la riguardano. Le grandi civiltà dell'antichità hanno lasciato registrazioni di coloni, tasse raccolte, quantità di raccolti e dimensioni degli eserciti.
Ad esempio, durante il suo lungo regno, Ramses II (1279-1213 a.C.) ordinò un censimento delle terre e degli abitanti dell'Egitto, che a quel punto contava circa 2 milioni di abitanti.
Allo stesso modo, la Bibbia narra che Mosè effettuò un censimento per scoprire quanti soldati avevano le dodici tribù di Israele.
Anche nell'antica Grecia si contavano persone e risorse. I romani, notevoli per la loro alta organizzazione, registravano periodicamente la popolazione, redigendo censimenti ogni cinque anni, comprensivi di territori e risorse..
Rinascimento
Dopo il declino di Roma, i record statistici importanti erano scarsi, fino all'arrivo del Rinascimento, quando la statistica riemerse come aiuto nel processo decisionale.
Alla fine del XVII secolo nacque la teoria delle probabilità, frutto della propensione delle persone per i giochi d'azzardo, che diede alla Statistica il rigore matematico che ne fece una scienza a sé stante.
Età moderna
Un nuovo impulso arrivò con la teoria degli errori e dei minimi quadrati nel XIX secolo, seguita dal metodo della correlazione tra variabili, per valutare quantitativamente la relazione tra loro..
Fino alla fine, durante il 20 ° secolo, la statistica si è diffusa in ogni branca della scienza e dell'ingegneria come strumento indispensabile per risolvere i problemi..
Caratteristiche statistiche descrittive
Le statistiche descrittive sono caratterizzate da:
- Organizza le informazioni raccolte sotto forma di dati e grafici. I grafici possono essere diversi: istogrammi, poligoni di frequenza, diagrammi a forma di torta, tra gli altri..
- Distribuire i dati in intervalli di frequenza per facilitarne la gestione. Utilizzare l'aritmetica per trovare i valori più rappresentativi dei dati, attraverso misure di tendenza centrale, nonché analizzare la loro dispersione.
- Determina la forma delle distribuzioni, la loro simmetria, se sono centrate o inclinate e se sono appuntite o piuttosto appiattite.
A cosa servono le statistiche descrittive?
Ogni volta che i dati devono essere raccolti, organizzati e presentati, le statistiche descrittive sono essenziali nelle aree della scienza che trattano molti elementi e quantità, così come in gran parte delle attività umane: economia, politica, salute, sport e altro ancora..
Ecco alcuni esempi:
Economia
Le statistiche descrittive si occupano di registrare e organizzare in modo coerente i dati sulle popolazioni e sulla loro età, reddito, investimenti, guadagni e spese. In questo modo, i governi e le istituzioni pianificano miglioramenti e investono risorse in modo appropriato..
Con il suo aiuto vengono monitorati gli acquisti, le vendite, i resi e l'efficienza dei servizi. Per questo motivo, le statistiche sono essenziali nel processo decisionale.
Fisica e Meccanica
La fisica e la meccanica utilizzano le statistiche per studiare i mezzi continui, che consistono in un gran numero di particelle, come atomi e molecole. Si scopre che non è possibile tenere traccia di ciascuno di essi separatamente..
Ma studiando il comportamento globale del sistema (una porzione di gas, ad esempio) dal punto di vista macroscopico, è possibile trovare medie e definire variabili macroscopiche per conoscerne le proprietà. Un esempio di ciò è la teoria cinetica dei gas.
Medicinale
È uno strumento essenziale per monitorare le malattie, dalla loro origine e durante la loro evoluzione, nonché l'efficacia dei trattamenti.
Le statistiche che descrivono i tassi di morbilità, i tassi di guarigione, i tempi di incubazione o di sviluppo di una malattia, l'età in cui si manifesta di solito e dati simili, sono necessari quando si progettano i trattamenti più efficaci..
Nutrizione
Una delle tante applicazioni della statistica descrittiva è quella di registrare e ordinare i dati sul consumo di cibo in diverse popolazioni: la sua quantità, qualità e quali sono i più consumati, tra molte altre osservazioni che interessano gli esperti..
Esempi di statistiche descrittive
Di seguito sono riportati alcuni esempi che illustrano quanto siano utili gli strumenti di statistica descrittiva per aiutare a prendere decisioni:
Esempio 1

Le autorità educative di un paese pianificano miglioramenti istituzionali. Supponi di voler implementare un nuovo sistema di mense scolastiche.
Per questo, è necessario disporre di dati sulla popolazione studentesca, ad esempio il numero di studenti per classe, la loro età, sesso, altezza, peso e condizione socioeconomica. Queste informazioni vengono quindi presentate sotto forma di tabelle e grafici..
Esempio 2
Per tenere traccia della squadra di calcio locale e fare nuovi acquisti, i manager tengono traccia del numero di partite giocate, vinte, pareggiate e perse, nonché del numero di gol, dei marcatori e di come sono riusciti a segnare: calcio di punizione, metà tribunale, sanzioni, con la gamba sinistra o destra, tra gli altri dettagli.
Esempio 3
Una gelateria ha diversi gusti di gelato e vuole migliorare le sue vendite, quindi i proprietari effettuano uno studio dove contano il numero di clienti, li separano in gruppi per sesso e fascia di età.
In questo studio, ad esempio, vengono registrati il gusto di gelato preferito e la presentazione più venduta. E con i dati raccolti, pianificano gli acquisti dei gusti e dei contenitori e degli accessori necessari alla loro preparazione..
Nozioni di base sulla statistica descrittiva
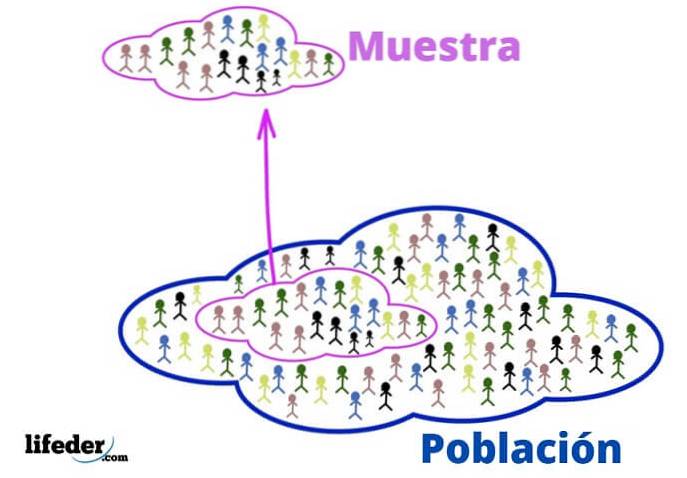
Questi concetti fondamentali sono necessari per applicare tecniche statistiche, vediamo:
Popolazione
Nel contesto statistico, la popolazione si riferisce all'universo o al gruppo da cui provengono le informazioni.
Non riguardano sempre le persone, poiché possono essere gruppi di animali, piante o oggetti come automobili, atomi, molecole e persino eventi e idee..
Mostrare
Quando la popolazione è molto numerosa, viene prelevato e analizzato un campione rappresentativo, senza perdere le informazioni rilevanti..
Può essere scelto a caso, o secondo alcuni criteri precedentemente stabiliti dall'analista. Il vantaggio è che essendo un sottoinsieme della popolazione, è molto più gestibile.
Variabile
Si riferisce all'insieme di valori che può assumere una certa caratteristica della popolazione. Uno studio può contenere diverse variabili, come età, sesso, peso, livello accademico, stato civile, reddito, temperatura, colore, ora e molte altre.
Le variabili possono essere di diversa natura, quindi ci sono criteri per classificarle e dare loro il trattamento più appropriato.
Variabili categoriali e variabili numeriche
A seconda del modo in cui vengono misurate, le variabili possono essere:
-Categorico
-Numerico
Variabili categoriali, chiamate anche qualitativo, rappresentano qualità come lo stato civile di una persona, che può essere single, sposata, divorziata o vedova.
Invece, variabili numeriche o quantitativa, possono essere misurati, come età, tempo, peso, reddito e altro.
Variabili discrete e variabili continue
Le variabili discrete accettano solo valori discreti, come suggerisce il nome. Ne sono un esempio il numero di bambini in una famiglia, quante materie ci sono in un certo corso e il numero di auto in un parcheggio.
Queste variabili non assumono sempre valori interi, poiché esistono anche valori frazionari.
D'altra parte, le variabili continue ammettono valori infiniti all'interno di un certo intervallo, come il peso di una persona, il pH del sangue, il tempo di una consultazione telefonica e il diametro dei palloni da calcio..
Misure di tendenza centrale
Danno un'idea della tendenza generale seguita dai dati. Citeremo le tre misure centrali più utilizzate:
-Metà
-Mediano
-moda
Metà
Equivalente alla media dei valori. Viene calcolato sommando tutte le osservazioni e dividendo per il numero totale:

moda
È il valore che viene ripetuto di più in un set di dati, il più o il più frequente, poiché in una distribuzione possono esserci più di una modalità.
Mediano
Quando si ordina un insieme di dati, la mediana è il valore centrale di tutti loro.
Misure di dispersione
Sottolineano la variabilità dei dati e danno un'idea di quanto siano lontani o dispersi dalle misure centrali. I più utilizzati sono:
Rango
È la differenza tra il valore più grande xM e la più piccola xm da un set di dati:
Rango = xM - Xm
Varianza
Misura la distanza dei dati dal valore medio. Per fare ciò, viene effettuata una media, ma con le differenze tra qualsiasi valore xio e il mezzo, squadrare per evitare che si annullino a vicenda. Di solito è indicato dalla lettera greca σ al quadrato o con sDue:

La varianza non ha le stesse unità dei dati, quindi la deviazione standard è definita come la radice quadrata della varianza ed è indicata come σ o s:

Invece di prendere in considerazione ogni dato individualmente, è preferibile raggrupparli in intervalli, il che facilita il lavoro, soprattutto se ci sono molti valori. Ad esempio, quando si lavora con i bambini in una scuola, possono essere raggruppati in fasce di età: da 0 a 6 anni, da 6 a 12 anni e da 12 a 18 anni.
Grafici
Sono un ottimo modo per vedere la distribuzione dei dati a colpo d'occhio e contengono tutte le informazioni raccolte nelle tabelle e nelle tabelle, ma molto più convenienti.
Ce n'è una grande varietà: con barre, lineari, circolari, gambo e foglia, istogrammi, poligoni di frequenza e pittogrammi. Esempi di grafici statistici sono mostrati nella Figura 3..
Temi di interesse
Rami di statistica.
Variabili statistiche.
Popolazione e campione.
Statistica inferenziale.
Riferimenti
- Faraldo, P. Statistica e metodologia della ricerca. Recupero da: eio.usc.es.
- Fernández, S. 2002. Statistiche descrittive. 2 °. Edizione. Editoriale ESIC. Recupero da: Google Libri.
- Storia della statistica. Estratto da: eumed.net.
- Ibañez, P. 2010. Matematica II. Approccio alla competenza. Cengage Learning.
- Monroy, S. 2008. Statistiche descrittive. 1 °. Edizione. Istituto Politecnico Nazionale del Messico.
- Formule dell'universo. Statistiche descrittive. Estratto da: universoformulas.com.

Nessun utente ha ancora commentato questo articolo.