
Unità di energia libera di Gibbs, come calcolarla, esercizi risolti
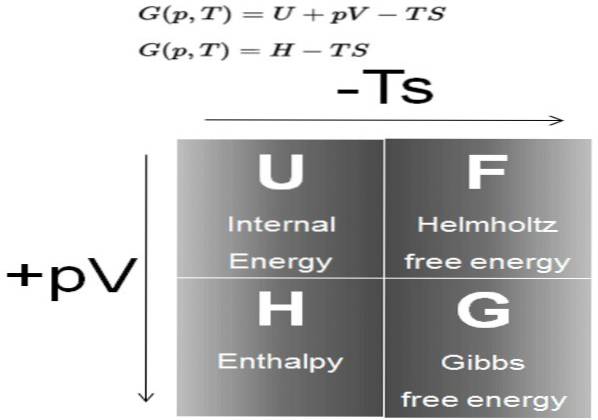
Il Energia libera di Gibbs (comunemente chiamato G) è un potenziale termodinamico definito come la differenza dell'entalpia H, meno il prodotto della temperatura T, dall'entropia S del sistema:
G = H - T S
L'energia libera di Gibbs è misurata in Joule (secondo il Sistema Internazionale), in erg (per il Sistema di unità cegesimale), in calorie o in elettronvolt (per elettro Volt).
Nei processi che avvengono a pressione e temperatura costanti, la variazione dell'energia libera di Gibbs è ΔG = ΔH - T ΔS. In tali processi, (G) rappresenta l'energia disponibile nel sistema che può essere convertita in lavoro.
Ad esempio, nelle reazioni chimiche esotermiche, l'entalpia diminuisce mentre l'entropia aumenta. Nella funzione di Gibbs questi due fattori vengono contrastati, ma solo quando l'energia di Gibbs diminuisce la reazione avviene spontaneamente..
Quindi, se la variazione di G è negativa, il processo è spontaneo. Quando la funzione di Gibbs raggiunge il suo minimo, il sistema raggiunge uno stato di equilibrio stabile. In sintesi, in un processo per il quale la pressione e la temperatura rimangono costanti, possiamo affermare:
- Se il processo è spontaneo, allora ΔG < 0
- Quando il sistema è in equilibrio: ΔG = 0
- In un processo non spontaneo G aumenta: ΔG> 0.
Indice articolo
- 1 Come viene calcolato?
- 1.1 - Passo dopo passo
- 1.2 - Relazioni termodinamiche di Maxwell
- 2 Esercizi risolti
- 2.1 Esercizio 1
- 2.2 Esercizio 2
- 2.3 Esercizio 3
- 3 Riferimenti
Come viene calcolato?
L'energia libera di Gibbs (G) viene calcolata utilizzando la definizione data all'inizio:
G = H - T⋅S
A sua volta, l'entalpia H è un potenziale termodinamico definito come:
H = U + P V
- Passo dopo passo
Successivamente, verrà effettuata un'analisi passo passo, per conoscere le variabili indipendenti di cui l'energia di Gibbs è una funzione:
1- Dalla prima legge della termodinamica abbiamo che l'energia interna U è correlata all'entropia S del sistema e al suo volume V per processi reversibili attraverso la relazione differenziale:
dU = dQ - dW = TdS - PdV
Da questa equazione segue che l'energia interna U è una funzione delle variabili S e V:
U = U (S, V)
2- Partendo dalla definizione di H e prendendo il differenziale, si ottiene:
dH = dU + d (P V) = dU + VdP + PdV
3- Sostituendo l'espressione per dU ottenuta in (1) abbiamo:
dH = TdS - PdV + VdP + PdV = TdS + VdP
Da ciò si conclude che l'entalpia H dipende dall'entropia S e dalla pressione P, cioè:
H = H (S, P)
4- Si calcola ora il differenziale totale dell'energia libera di Gibbs ottenendo:
dG = dH -TdS -SdT = TdS + VdP -TdS -SdT
Dove dH è stata sostituita dall'espressione trovata in (3).
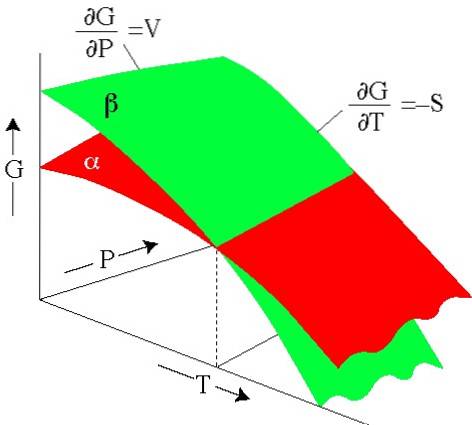
5- Infine, semplificando, otteniamo: dG = VdP - SdT, essendo chiaro che l'energia libera G dipende dalla pressione e dalla temperatura T in quanto:
G = G (P, T)
- Le relazioni termodinamiche di Maxwell
Dall'analisi della sezione precedente, segue che l'energia interna di un sistema è una funzione dell'entropia e del volume:
U = U (S, V)
Quindi il differenziale di O sarà:
dU = ∂SU |V dS + ∂VU |S dV = TdS - PdV
Da questa espressione derivata parziale, si possono derivare le cosiddette relazioni termodinamiche di Maxwell. Le derivate parziali si applicano quando una funzione dipende da più di una variabile e sono facilmente calcolate applicando il teorema nella sezione successiva.
La prima relazione di Maxwell
∂VT |S = -∂SP |V
Per arrivare a questa relazione, il Teorema di Clairaut-Schwarz sulle derivate parziali, che afferma quanto segue:
"Le derivate miste di secondo ordine con le variabili intercambiate sono uguali, purché le funzioni da derivare siano continue e differenziabili".
La seconda relazione di Maxwell
In base a quanto riportato al punto 3 della sezione precedente:
H = H (S, P) e dH = TdS + VdP
Si può ottenere:
∂PT |S = ∂SV |P
Procediamo in modo simile con Gibbs free energy G = G (P, T) e con Helmholtz free energy F = F (T, V) per ottenere le altre due relazioni termodinamiche di Maxwell.

Le quattro relazioni termodinamiche di Maxwell
1- Associato all'energia interna U: ∂VT |S = -∂SP |V
2- Quello ottenuto dall'entalpia H: ∂PT |S = ∂SV |P
3- Relativo all'energia di Helmholtz F: ∂TP |V = ∂VS |T
4- Collegato all'energia libera Gibbs G: ∂TV |P = -∂PS |T
Esercizi risolti
Esercizio 1
Calcola la variazione dell'energia libera di Gibbs per 2 moli di gas ideale alla temperatura di 300K durante un'espansione isotermica che porta il sistema da un volume iniziale di 20 litri ad un volume finale di 40 litri.
Soluzione
Ricordando la definizione di energia libera di Gibbs abbiamo:
G = H - T S
Allora una variazione finita di F sarà:
ΔG = ΔH - T ΔS, poiché ΔT = 0
Nei gas ideali, l'entalpia dipende solo dalla sua temperatura assoluta, ma poiché è un processo isotermico, allora ΔH = 0 e ΔG = - T ΔS.
Per i gas ideali la variazione di entropia di un processo isotermico è:
ΔS = nR ln (VDue/ V1)
Quello applicato al caso di questo esercizio rimane:
ΔS = 2 moli x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Quindi possiamo ottenere il cambiamento nell'energia di Helmholtz:
ΔG = - 300K x 11,53 J / K = -3457,70 J.
Esercizio 2
Tenendo conto che l'energia libera di Gibbs è funzione della temperatura e della pressione G = G (T, P); determinare la variazione di G durante un processo in cui la temperatura non cambia (isotermica) per n moli di un gas ideale monoatomico.
Soluzione
Come dimostrato sopra, la variazione dell'energia di Gibbs dipende solo dalla variazione della temperatura T e del volume V, quindi una sua variazione infinitesimale viene calcolata in base a:
dG = -SdT + VdP
Ma se è un processo in cui la temperatura è costante allora dF = + VdP, quindi una variazione di pressione finita ΔP porta ad una variazione nell'energia di Gibbs data da:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = + n R T ln (ΔP)
Utilizzando l'equazione del gas ideale:
P V = n R T
Durante un processo isotermico si verifica che:
d (P V) = P dV + V dP = 0
Questo è:
dP / P = - dV / V
Quindi il risultato di cui sopra può essere scritto in funzione della variazione di volume ΔV:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = - ∫ (n R T) dV / V = -n R T ln (ΔV)
Esercizio 3
Considerando la seguente reazione chimica:
NDue0 (g) + (3/2) ODue (g) ↔️ 2NODue (g) alla temperatura T = 298 K
Trova la variazione dell'energia libera di Gibbs e, utilizzando il risultato ottenuto, indica se si tratta o meno di un processo spontaneo.
Soluzione
Ecco i passaggi:
- Fase uno: entalpie di reazione
ΔHr = 2 * ΔH (NODue (g)) - ΔH (NDue0 (g)) = 2 * 33,2-81,6 = -15,2 kJ / mol
- Seconda fase: la variazione dell'entropia di reazione
ΔSr = 2 * S (NODue (g)) - S (NDue0 (g)) - (3/2) S (ODue (g)) = 2 * 240,1 - 220,1 - 1,5 * 205,2 = -47,7 J / (mol * K).
- Terzo passo: variazione della funzione di Gibbs
Questo valore determinerà l'equilibrio tra l'energia decrescente e l'entropia crescente per sapere se alla fine la reazione è spontanea o meno.
ΔGr = ΔHr - T ΔSr = -15,2 -298 * (- 47,7) = -985,4 J / mol
Trattandosi di una variazione negativa dell'energia di Gibbs, si può concludere che si tratta di una reazione spontanea alla temperatura di 298 K = 25 ºC.
Riferimenti
- Castagne E. Esercizi di energia libera. Estratto da: lidiaconlaquimica.wordpress.com.
- Cengel, Y. 2012. Termodinamica. 7a edizione. Mcgraw hill.
- Libretexts. Gibbs Free Energy. Recupero da: chem.libretexts.org
- Libretexts. Cosa sono le energie libere. Recupero da: chem.libretexts.org
- Wikipedia. Energia libera di Gibbs. Estratto da: es.wikipedia.com
- Wikipedia. Energia libera di Gibbs. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.