
Formule, caratteristiche, applicazioni, esercizi per l'energia gravitazionale
Il energia gravitazionale È quello che ha un oggetto massiccio quando è immerso nel campo gravitazionale prodotto da un altro. Alcuni esempi di oggetti con energia gravitazionale sono: la mela nell'albero, la mela che cade, la Luna in orbita attorno alla Terra e la Terra in orbita attorno al Sole.
Isaac Newton (1642-1727) è stato il primo a rendersi conto che la gravità è un fenomeno universale e che ogni oggetto con massa nel suo ambiente produce un campo in grado di produrre una forza su un altro.

Indice articolo
- 1 Formule ed equazioni
- 2 Caratteristiche dell'energia gravitazionale
- 2.1 Campo gravitazionale e potenziale
- 3 Applicazioni
- 3.1 Potenziale gravitazionale della Terra
- 3.2 Energia potenziale vicino alla superficie terrestre
- 4 esercizi
- 4.1 Esercizio 1: collasso gravitazionale della Terra
- 4.2 Esercizio 2: Collasso gravitazionale e velocità di fuga
- 4.3 Esercizio 3: Energia gravitazionale della mela
- 5 Riferimenti
Formule ed equazioni
La forza a cui si riferiva Newton è nota come forza gravitazionale e fornisce energia all'oggetto su cui agisce. Newton ha formulato la legge di gravitazione universale come segue:
"Siano due oggetti puntiformi di masse m1 e m2 rispettivamente, ciascuno esercita sull'altro una forza di attrazione proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza che li separa".
Energia gravitazionale O associato alla forza gravitazionale F è:

Un oggetto immerso in un campo gravitazionale ha energia potenziale gravitazionale O ed energia cinetica K. Se non ci sono altre interazioni, o se sono di intensità trascurabile, l'energia totale E di detto oggetto è la somma della sua energia gravitazionale più la sua energia cinetica:
E = K + U
Se un oggetto si trova in un campo gravitazionale e non sono presenti altre forze dissipative, come l'attrito o la resistenza dell'aria, l'energia totale E è una quantità che rimane costante durante il movimento.
Caratteristiche dell'energia gravitazionale
- Un oggetto ha energia potenziale gravitazionale se è solo in presenza del campo gravitazionale prodotto da un altro.
- L'energia gravitazionale tra due oggetti aumenta all'aumentare della distanza di separazione tra loro.
- Il lavoro svolto dalla forza gravitazionale è uguale e contrario alla variazione dell'energia gravitazionale della posizione finale rispetto a quella della sua posizione iniziale..
- Se un corpo è soggetto solo all'azione della gravità, la variazione della sua energia gravitazionale è uguale e contraria alla variazione della sua energia cinetica..
- L'energia potenziale di un oggetto di massa m che è ad un'altezza h rispetto alla superficie terrestre è mgh volte maggiore dell'energia potenziale in superficie, essere g l'accelerazione di gravità, per le altezze h molto più piccolo del raggio terrestre.
Campo gravitazionale e potenziale
Il campo gravitazionale g è definita come la forza gravitazionale F per unità di massa. Viene determinato posizionando una particella di prova m in ogni punto dello spazio e calcolando il quoziente tra la forza che agisce sulla particella di prova diviso per il valore della sua massa:
g = F / m
Il potenziale gravitazionale V di un oggetto di massa m è definito come l'energia potenziale gravitazionale di quell'oggetto divisa per la propria massa.
Il vantaggio di questa definizione è che il potenziale gravitazionale dipende solo dal campo gravitazionale, quindi una volta che il potenziale è noto V, energia gravitazionale O di un oggetto di massa m è:
U = m.V

Applicazioni
L'energia potenziale gravitazionale è quella immagazzinata dai corpi quando si trovano in un campo gravitazionale.
Ad esempio, l'acqua contenuta in un serbatoio ha più energia poiché il serbatoio è più alto..
Maggiore è l'altezza della vasca, maggiore è la velocità dell'acqua in uscita dal rubinetto. Ciò è dovuto al fatto che l'energia potenziale dell'acqua all'altezza della vasca si trasforma in energia cinetica dell'acqua all'uscita del rubinetto..
Quando l'acqua viene arginata in cima a una montagna, l'energia potenziale può essere sfruttata per attivare le turbine di generazione di energia..
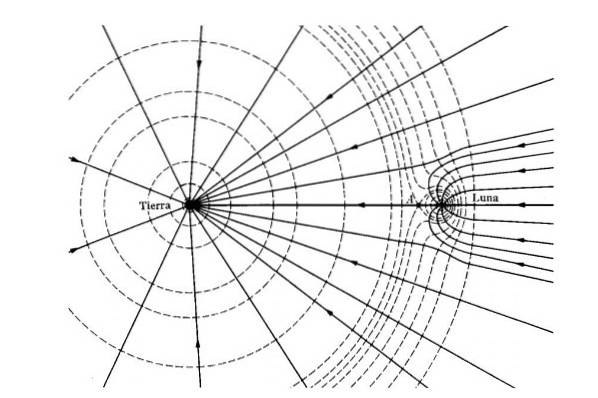
L'energia gravitazionale spiega anche le maree. Poiché l'energia e la forza gravitazionale dipendono dalla distanza, l'attrazione gravitazionale della Luna è maggiore sulla faccia della Terra più vicina alla Luna rispetto alla faccia più lontana e opposta..
Questo produce una differenza di forze che deforma la superficie del mare. L'effetto è maggiore in una luna nuova, quando il Sole e la Luna sono allineati.
La possibilità di costruire stazioni spaziali e satelliti che rimangano relativamente vicini al nostro pianeta è dovuta all'energia gravitazionale prodotta dalla Terra. Altrimenti, le stazioni spaziali e i satelliti artificiali vagherebbero nello spazio.
Il potenziale gravitazionale della Terra
Supponiamo che la Terra abbia massa M e un oggetto che è al di sopra della superficie terrestre in lontananza r rispetto al centro ha massa m.
In questo caso il potenziale gravitazionale è determinato dall'energia gravitazionale dividendola semplicemente per la massa dell'oggetto risultando:

Energia potenziale vicino alla superficie terrestre
Supponiamo che la Terra abbia un raggio RT e massa M.
Anche se la Terra non è un oggetto puntuale, il campo sulla sua superficie è equivalente a quello che si otterrebbe se avesse tutta la sua massa M era concentrato al centro, in modo che l'energia gravitazionale di un oggetto all'altezza h sopra la superficie terrestre sia
U (RT + h) = -G.M m (RT + h) ^ - 1
Ma poiché h è molto inferiore a RT, l'espressione sopra può essere approssimata da
U = Uo + mgh
Dove g è l'accelerazione di gravità, il cui valore medio per la Terra è 9,81 m / s ^ 2.
Allora l'energia potenziale Ep di un oggetto di massa m all'altezza h sopra la superficie terrestre è:
Ep (h) = U + Uo = mgh
Sulla superficie terrestre h = 0, quindi un oggetto sulla superficie ha Ep = 0. Calcoli dettagliati possono essere visti nella figura 3.

Formazione
Esercizio 1: collasso gravitazionale della Terra
Supponiamo che il nostro pianeta subisca un collasso gravitazionale a causa della perdita di energia termica al suo interno e il suo raggio scenda alla metà del suo valore attuale ma la massa del pianeta rimanga costante..
Determina quale sarebbe l'accelerazione di gravità vicino alla superficie della Nuova Terra e quanto peserebbe un sopravvissuto del peso di 50 kg-f prima del collasso. Aumenta o diminuisci l'energia gravitazionale della persona e in base a quale fattore.
Soluzione
L'accelerazione di gravità sulla superficie di un pianeta dipende dalla sua massa e dal suo raggio. La costante di gravitazione è universale e funziona allo stesso modo per pianeti ed esopianeti.
Nel caso presente, se il raggio della Terra fosse ridotto della metà, l'accelerazione di gravità della Nuova Terra sarebbe 4 volte maggiore. I dettagli possono essere visti nella seguente scheda.

Ciò significa che un superuomo e sopravvissuto che pesava 50 kg-f sul vecchio pianeta peserà 200 kg-f sul nuovo pianeta..
D'altra parte, l'energia gravitazionale sarà stata dimezzata sulla superficie del nuovo pianeta..
Esercizio 2: collasso gravitazionale e velocità di fuga
In riferimento alla situazione presentata nell'esercizio 1, cosa accadrebbe alla velocità di fuga: aumenta, diminuisce, di quale fattore?
Soluzione 2
La velocità di fuga è la velocità minima necessaria per sfuggire all'attrazione gravitazionale di un pianeta.
Per calcolarlo, si presume che un proiettile sparato con questa velocità raggiunga l'infinito con velocità zero. Inoltre, all'infinito l'energia gravitazionale è zero. Pertanto un proiettile che viene sparato con velocità di fuga avrà un'energia totale pari a zero.
In altre parole, sulla superficie del pianeta al momento dello sparo, la somma dell'energia cinetica del proiettile + l'energia gravitazionale deve essere zero:
½ m Ve ^ 2 - (G M.m) / RT = 0
Si noti che la velocità di fuga non dipende dalla massa del proiettile e il suo valore al quadrato è
Ve ^ 2 = (2G M) / RT
Se il pianeta collassa a una metà del raggio dell'originale, il quadrato della nuova velocità di fuga diventa doppio.
Pertanto la nuova velocità di fuga cresce e diventa 1,41 volte la vecchia velocità di fuga:
Vai '= 1,41 Vai
Esercizio 3: Energia gravitazionale della mela
Un ragazzo sul balcone di un edificio a 30 metri dal suolo fa cadere una mela da 250 g, che dopo pochi secondi raggiunge il suolo.

a) Qual è la differenza di energia gravitazionale della mela in alto rispetto alla mela a livello del suolo?
b) Quanto era veloce la mela appena prima di cadere a terra?
c) Cosa succede all'energia una volta che la mela è appiattita contro il terreno?
Soluzione
a) La differenza di energia gravitazionale è
m.g. h = 0,250 kg * 9,81 m / s ^ 2 * 30 m = 73,6 J
b) L'energia potenziale che aveva la mela quando era alta 30 m si trasforma in energia cinetica nel momento in cui la mela raggiunge il suolo.
½ m v ^ 2 = m.g.h
v ^ 2 = 2.g.h
Sostituendo i valori e risolvendo, ne consegue che la mela raggiunge il suolo con una velocità di 24,3 m / s = 87,3 km / h.
c) Ovviamente la mela si disperde e tutta l'energia gravitazionale accumulata all'inizio si perde sotto forma di calore, poiché i pezzi di mela e la zona d'urto si riscaldano, inoltre parte dell'energia viene dissipata anche sotto forma di suono onde "splash".
Riferimenti
- Alonso, M. (1970). Fisica Vol. 1, Fondo educativo interamericano.
- Hewitt, Paul. 2012. Scienze fisiche concettuali. 5 °. Ed. Pearson.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, F. (2009). University Physics Vol. 1
- Wikipedia. Energia gravitazionale. Estratto da: es.wikipedia.com
- Wikipedia. Energia gravitazionale. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.