
Proprietà eneagon, come creare un enegono, esempi

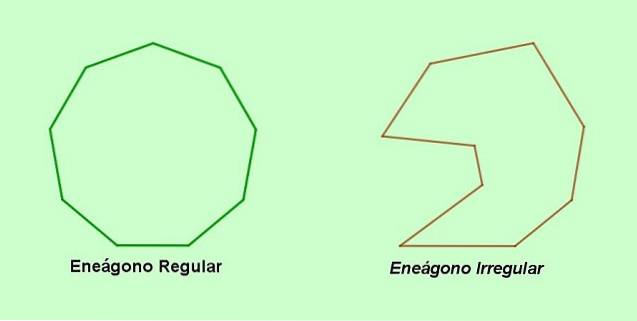
UN eneagon è un poligono con nove lati e nove vertici, che può essere regolare o meno. Il nome eneágono deriva dal greco e si compone delle parole greche ennea (nove e gonon (angolo).
Un nome alternativo per il poligono a nove lati è nonagon, una parola che deriva dal latino nonus (nove e gonon (vertice). D'altra parte, se i lati o gli angoli dell'enegon non sono uguali tra loro, allora abbiamo un enegon irregolare. Se, d'altra parte, i nove lati e i nove angoli dell'enegon sono uguali, allora è a enegon regolare.
Indice articolo
- 1 Proprietà dell'enegon
- 1.1 Enegon regolare
- 1.2 Area di un enegon noto il lato e l'apotema
- 1.3 Area di un enegon noto sul lato
- 1.4 Perimetro del normale enegon noto il suo lato
- 1.5 Perimetro dell'enegon noto il suo raggio
- 2 Come fare un enegone regolare
- 3 esempi
- 3.1 Esempio 1
- 3.2 Esempio 2
- 4 Riferimenti
Proprietà Eneagon
Per un poligono con n lati la somma dei suoi angoli interni è:
(n - 2) * 180º
Nell'enegon sarebbe n = 9, quindi la somma dei suoi angoli interni è:
Sa = (9 - 2) * 180º = 7 * 180º = 1260º
In ogni poligono, il numero di diagonali è:
D = n (n - 3) / 2 e nel caso dell'enegon, poiché n = 9, abbiamo allora che D = 27.
Enegon regolare
Nell'enagono o nonagono regolare ci sono nove (9) angoli interni di uguale misura, quindi ogni angolo misura un nono della somma totale degli angoli interni.
La misura degli angoli interni di un enegon è quindi 1260º / 9 = 140º.
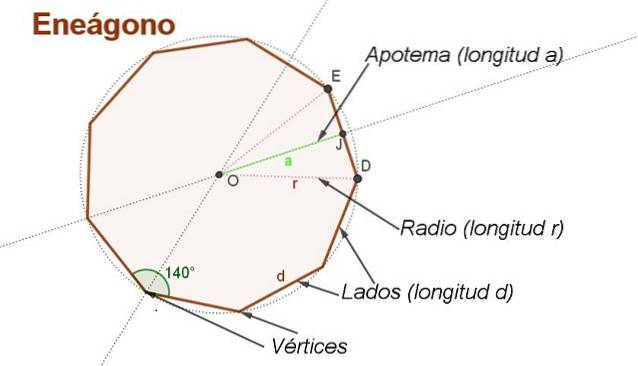
Per derivare la formula per l'area di un enegon regolare con lato d è conveniente realizzare alcune costruzioni ausiliarie, come quelle mostrate in figura 2.
Il centro si trova O tracciando le bisettrici di due lati adiacenti. Il centro O equidistante dai vertici.
Un raggio di lunghezza r è il segmento che va dal centro O a un vertice dell'enegon. I raggi sono mostrati in figura 2. OD Y OE di lunghezza r.
L'apotema è il segmento che va dal centro al punto medio di un lato dell'enegon. Per esempio GU è un apotema la cui lunghezza è per.
Area di un noto enegon il lato e l'apotema
Consideriamo il triangolo ODE di figura 2. L'area di questo triangolo è il prodotto della sua base A PARTIRE DAL per l'altezza GU diviso per 2:
La zona ODE = (DE * GU) / 2 = (d * a) / 2
Poiché ci sono 9 triangoli di uguale area nell'enegon, si conclude che l'area dello stesso è:
Zona Eneagon = (9/2) (d * a)
Area di un noto enegon laterale
Se si conosce solo la lunghezza d dei lati dell'enegon, è necessario trovare la lunghezza dell'apotema per poter applicare la formula della sezione precedente.
Consideriamo il triangolo OCCHIO rettangolo in J (vedi figura 2). Se si applica il rapporto trigonometrico tangente, si ottiene:
così(∡OEJ) = GU / Ex.
L'angolo ∡OEJ = 140º / 2 = 70º, essere EO bisettrice dell'angolo interno dell'enegon.
D'altro canto, GU è l'apotema della lunghezza per.
Quindi come J è il punto medio di ED ne consegue che EJ = d / 2.
Sostituendo i valori precedenti nella relazione tangente abbiamo:
tan (70º) = a / (d / 2).
Ora cancelliamo la lunghezza dell'apotema:
a = (d / 2) tan (70º).
Il risultato precedente viene sostituito nella formula dell'area per ottenere:
Zona Eneagon = (9/2) (d * a) = (9/2)( d * (d / 2) tan (70º))
Infine troviamo la formula che permette di ottenere l'area dell'enegone regolare se si conosce solo la lunghezza d dai suoi lati:
Zona Eneagon = (9/4) dDue tan (70º) = 6,1818 dDue
Perimetro di enegon regolare noto il suo lato
Il perimetro di un poligono è la somma dei suoi lati. Nel caso dell'enegon, poiché ognuno dei lati misura una lunghezza d, il suo perimetro sarà la somma di nove volte d, vale a dire:
Perimetro = 9 d
Il perimetro dell'enegon conosceva il suo raggio
Considerando il triangolo OCCHIO rettangolo in J (vedi figura 2), viene applicato il rapporto coseno trigonometrico:
cos (∡OEJ) = Ex / OE = (d / 2) / r
Da dove si ottiene:
d = 2r cos (70º)
Sostituendo questo risultato, otteniamo la formula per il perimetro in funzione del raggio dell'enegone:
Perimetro = 9 d = 18 r cos (70º) = 6,1564 r
Come fare un enegone regolare
1- Per costruire un enegono regolare, con righello e compasso, partire dalla circonferenza c che circoscrive l'enegon. (vedi figura 3)
2- Due linee perpendicolari sono tracciate attraverso il centro O della circonferenza. Quindi le intersezioni A e B di una delle linee sono contrassegnate con la circonferenza.
3- Con il compasso, centrando all'intercetta B e apertura uguale al raggio BO, si traccia un arco che intercetta la circonferenza originaria in un punto C.
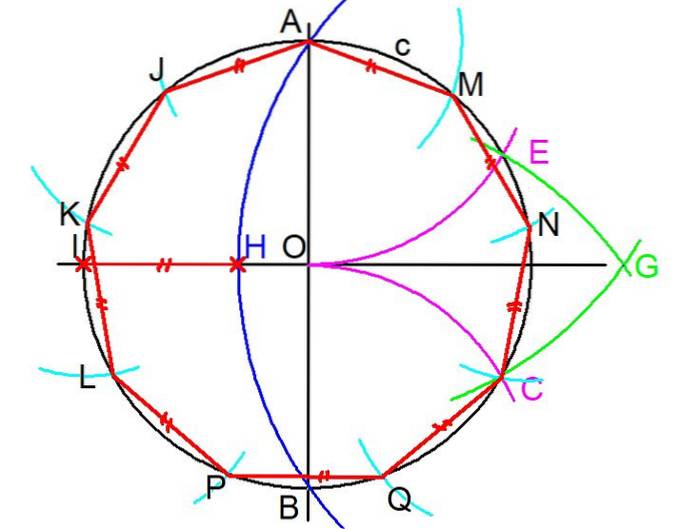
4- Si ripete il passaggio precedente ma realizzando un centro in A e raggio AO, si disegna un arco che intercetta la circonferenza c nel punto E.
5- Con l'apertura AC e il centro in A viene disegnato un arco di circonferenza. Allo stesso modo con l'apertura BE e il centro B viene disegnato un altro arco. L'intersezione di questi due archi è contrassegnata come punto G.
6- Centrando in G e aprendo GA, si traccia un arco che intercetta l'asse secondario (orizzontale in questo caso) nel punto H. L'intersezione dell'asse secondario con la circonferenza originale c è contrassegnata come I.
7- La lunghezza del segmento IH è uguale alla lunghezza d del lato dell'enegon.
8- Con apertura del compasso IH = d, gli archi del centro A raggio AJ, centro J raggio AK, centro K raggio KL e centro L raggio LP vengono disegnati in successione.
9- Allo stesso modo, partendo da A e dal lato destro, si disegnano archi di raggio IH = d che segnano i punti M, N, C e Q sulla circonferenza originale c.
10- Infine vengono disegnati i segmenti AJ, JK, KL, LP, AM, MN, NC, CQ e infine PB.
Va notato che il metodo di costruzione non è del tutto esatto, poiché si può verificare che l'ultimo lato PB è dello 0,7% più lungo degli altri lati. Ad oggi, non esiste un metodo di costruzione noto con un righello e un compasso accurati al 100%..
Esempi
Ecco alcuni esempi funzionanti.
Esempio 1
Vuoi costruire un enegon regolare i cui lati misurino 2 cm. Quale raggio deve avere la circonferenza che lo circoscrive, in modo che applicando la costruzione descritta in precedenza si ottenga il risultato desiderato?
Soluzione:
In una sezione precedente è stata dedotta la formula che mette in relazione il raggio r del cerchio circoscritto con il lato d di un enegone regolare:
d = 2r cos (70º)
Risolvendo per r dall'espressione precedente abbiamo:
r = d / (2 cos (70º)) = 1,4619 * d
Sostituendo il valore d = 2 cm nella formula precedente, si ottiene un raggio r di 2,92 cm.
Esempio 2
Qual è l'area di un enegon regolare con un lato di 2 cm?
Soluzione:
Per rispondere a questa domanda, dobbiamo fare riferimento alla formula, precedentemente mostrata, che ci permette di trovare l'area di un enegone noto dalla lunghezza d del suo lato:
Zona Eneagon = (9/4) dDue tan (70º) = 6,1818 dDue
Sostituendo d al suo valore di 2 cm nella formula precedente, otteniamo:
Zona Eneagon = 24,72 cm
Riferimenti
- C. E. A. (2003). Elementi di geometria: con esercizi e geometria del compasso. Università di Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematica 2. Grupo Editorial Patria.
- Liberato, K. (2007). Scopri i poligoni. Benchmark Education Company.
- Hendrik, V. (2013). Poligoni generalizzati. Birkhäuser.
- IGER. (s.f.). Matematica Primo semestre Tacaná. IGER.
- Jr. geometria. (2014). Poligoni. Lulu Press, Inc.
- Miller, Heeren e Hornsby. (2006). Matematica: ragionamento e applicazioni (decima edizione). Pearson Education.
- Patiño, M. (2006). Matematica 5. Editoriale Progreso.

Nessun utente ha ancora commentato questo articolo.