
Equazione generale di una retta la cui pendenza è uguale a 2/3
L'equazione generale di una retta L è la seguente: Ax + By + C = 0, dove A, B e C sono costanti, x è la variabile indipendente ee la variabile dipendente.
La pendenza di una retta, generalmente indicata dalla lettera m, che passa per i punti P = (x1, y1) e Q = (x0, y0) è il seguente quoziente m: = (y1-y0) / (x1 -x0 ).
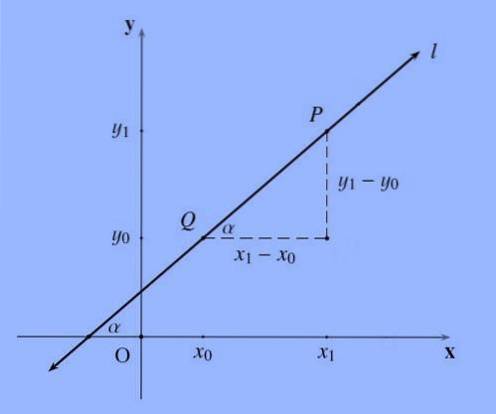
La pendenza di una linea, rappresenta in un certo modo l'inclinazione; Più formalmente, la pendenza di una linea è la tangente dell'angolo che forma con l'asse X..
Va notato che l'ordine in cui sono denominati i punti è indifferente, poiché (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).
Pendenza di una linea
Se sono noti due punti attraverso i quali passa una linea, è facile calcolarne la pendenza. Ma cosa succede se questi punti non sono noti?
Data l'equazione generale di una retta Ax + By + C = 0, la sua pendenza è m = -A / B.
Qual è l'equazione generale di una retta la cui pendenza è 2/3?
Poiché la pendenza della retta è 2/3, viene stabilita l'uguaglianza -A / B = 2/3, con la quale possiamo vedere che A = -2 e B = 3. Quindi l'equazione generale di una retta con pendenza pari a 2/3 è -2x + 3y + C = 0.
Va chiarito che se si scelgono A = 2 e B = -3 si otterrà la stessa equazione. In effetti, 2x-3y + C = 0, che è uguale al precedente moltiplicato per -1. Il segno di C non ha importanza in quanto è una costante generale.
Un'altra osservazione che si può fare è che per A = -4 e B = 6 si ottiene la stessa retta, nonostante la loro equazione generale sia diversa. In questo caso l'equazione generale è -4x + 6y + C = 0.
Esistono altri modi per trovare l'equazione generale della retta?
La risposta è si. Se la pendenza di una linea è nota, ci sono due modi, oltre al precedente, per trovare l'equazione generale.
Per questo, vengono utilizzate l'equazione Punto-Pendenza e l'equazione Shear-Pendenza..
-L'equazione punto-pendenza: se m è la pendenza di una linea e P = (x0, y0) un punto attraverso il quale passa, allora l'equazione y-y0 = m (x-x0) è chiamata equazione punto-pendenza.
-L'equazione di Shear-Slope: se m è la pendenza di una linea e (0, b) è il taglio della linea con l'asse Y, allora l'equazione y = mx + b è chiamata equazione di Shear-Slope.
Utilizzando il primo caso, si ottiene che l'equazione Punto-Pendenza di una retta la cui pendenza è 2/3 è data dall'espressione y-y0 = (2/3) (x-x0).
Per arrivare all'equazione generale, moltiplicare per 3 su entrambi i lati e tutti i termini vengono raggruppati su un lato dell'uguaglianza, con la quale si ottiene che -2x + 3y + (2 × 0-3y0) = 0 è l'equazione generale della linea, dove C = 2 × 0-3y0.
Se si utilizza il secondo caso, si ottiene che l'equazione Cut-Slope di una retta la cui pendenza è 2/3 è y = (2/3) x + b.
Ancora una volta, moltiplicando per 3 su entrambi i lati e raggruppando tutte le variabili, otteniamo -2x + 3y-3b = 0. Quest'ultima è l'equazione generale della retta dove C = -3b.
In realtà, guardando da vicino entrambi i casi, si può vedere che il secondo caso è semplicemente un caso particolare del primo (quando x0 = 0).
Riferimenti
- Fleming, W., & Varberg, D.E. (1989). Precalculus Mathematics. Prentice Hall PTR.
- Fleming, W., & Varberg, D.E. (1989). Matematica precalcolo: un approccio alla risoluzione dei problemi (2, illustrato ed.). Michigan: Prentice Hall.
- Kishan, H. (2005). Calcolo integrale. Editori e distributori Atlantic.
- Larson, R. (2010). Precalculus (8 ed.). Cengage Learning.
- Leal, J. M. e Viloria, N. G. (2005). Geometria analitica piana. Mérida - Venezuela: Editoriale Venezolana C. A.
- Pérez, C. D. (2006). Precalculation. Pearson Education.
- Saenz, J. (2005). Calcolo differenziale con le prime funzioni trascendenti per la scienza e l'ingegneria (Seconda edizione ed.). Ipotenusa.
- Sullivan, M. (1997). Precalculation. Pearson Education.



Nessun utente ha ancora commentato questo articolo.