
Caratteristiche della distribuzione F ed esercizi risolti
Il Distribuzione F. o La distribuzione di Fisher-Snedecor è quella utilizzata per confrontare le varianze di due popolazioni diverse o indipendenti, ciascuna delle quali segue una distribuzione normale.
La distribuzione che segue la varianza di un insieme di campioni da una singola popolazione normale è la distribuzione chi-quadrato (ΧDue) di grado n-1, se ciascuno dei campioni nell'insieme ha n elementi.
Per confrontare le varianze di due diverse popolazioni, è necessario definire un file statistica, cioè, una variabile casuale ausiliaria che ci permette di discernere se entrambe le popolazioni hanno o meno la stessa varianza.
Detta variabile ausiliaria può essere direttamente il quoziente delle varianze campionarie di ciascuna popolazione, nel qual caso, se detto quoziente è vicino all'unità, vi è evidenza che entrambe le popolazioni hanno varianze simili.
Indice articolo
- 1 La statistica F e la sua distribuzione teorica
- 1.1 Media, modo e varianza della distribuzione F.
- 2 Gestire la distribuzione F.
- 2.1 Tabelle della distribuzione F.
- 2.2 Software per la distribuzione F.
- 3 esercizi risolti
- 3.1 Esercizio 1
- 3.2 Esercizio 2
- 4 Riferimenti
La statistica F e la sua distribuzione teorica
La statistica della variabile casuale F o F proposta da Ronald Fisher (1890-1962) è quella più frequentemente utilizzata per confrontare le varianze di due popolazioni ed è definita come segue:
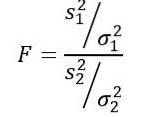
Essere sDue la varianza campionaria e σDue la varianza della popolazione. Per distinguere ciascuno dei due gruppi di popolazione, vengono utilizzati rispettivamente i pedici 1 e 2..
È noto che la distribuzione chi-quadro con (n-1) gradi di libertà è quella che segue la variabile ausiliaria (o statistica) definita di seguito:
XDue = (n-1) sDue / σDue.
Pertanto, la statistica F segue una distribuzione teorica data dalla seguente formula:
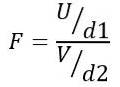
Essere O la distribuzione chi quadrato con d1 = n1 - 1 gradi di libertà per la popolazione 1 e V la distribuzione chi quadrato con d2 = n2 - 1 gradi di libertà per la popolazione 2.
Il quoziente definito in questo modo è una nuova distribuzione di probabilità, nota come Distribuzione F. con d1 gradi di libertà al numeratore e d2 gradi di libertà al denominatore.
Media, modo e varianza della distribuzione F.
Metà
La media della distribuzione F si calcola come segue:
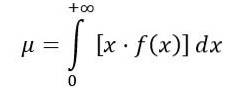
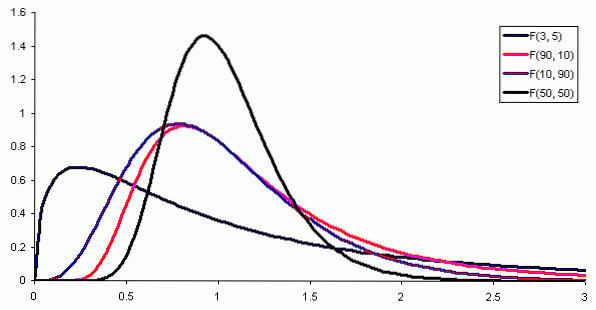
Dove f (x) è la densità di probabilità della distribuzione F, che è mostrata nella figura 1 per varie combinazioni di parametri o gradi di libertà.
Possiamo scrivere la densità di probabilità f (x) in funzione della funzione Γ (funzione gamma):
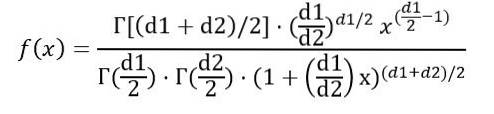
Eseguito l'integrale sopra indicato si conclude che la media della distribuzione F con gradi di libertà (d1, d2) è:
μ = d2 / (d2 - 2) con d2> 2
Dove si nota che, curiosamente, la media non dipende dai gradi di libertà d1 del numeratore.
moda
D'altra parte, la modalità dipende da d1 e d2 ed è data da:
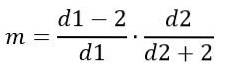
Per d1> 2.
Varianza della distribuzione F.
La varianza σDue della distribuzione F si calcola dall'integrale:
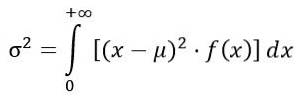
Ottenere:
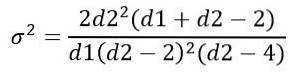
Gestire la distribuzione F.
Come altre distribuzioni di probabilità continue che coinvolgono funzioni complicate, la gestione della distribuzione F viene eseguita utilizzando tabelle o software..
Tabelle di distribuzione F
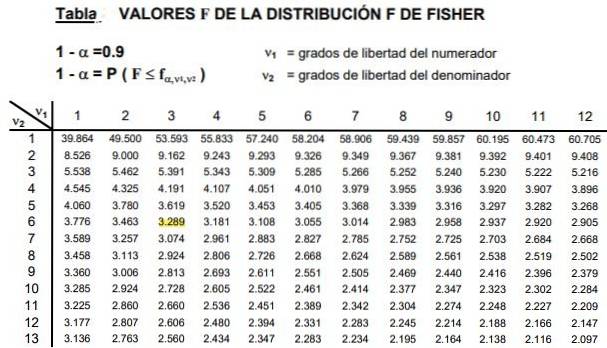
Le tabelle coinvolgono i due parametri o gradi di libertà della distribuzione F, la colonna indica il grado di libertà del numeratore e la riga il grado di libertà del denominatore.
La figura 2 mostra una sezione della tabella della distribuzione F per il caso di a livello di significatività del 10%, cioè α = 0,1. Il valore di F è evidenziato quando d1 = 3 e d2 = 6 con livello di confidenza 1- α = 0,9 che è il 90%.
Software per la distribuzione F.
Per quanto riguarda il software che gestisce la distribuzione F c'è una grande varietà, dai fogli di calcolo tale Eccellere a pacchetti specializzati come minitab, SPSS Y R per citarne alcuni tra i più noti.
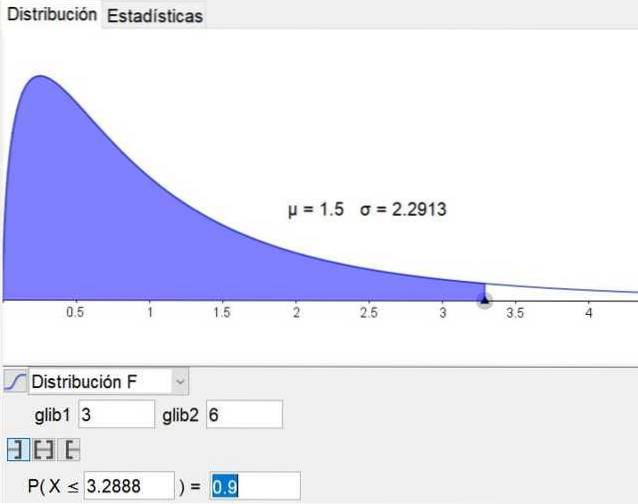
È interessante notare che il software di geometria e matematica geogebra ha uno strumento statistico che include le principali distribuzioni, inclusa la distribuzione F. La Figura 3 mostra la distribuzione F per il caso d1 = 3 e d2 = 6 con livello di confidenza del 90%.
Esercizi risolti
Esercizio 1
Considera due campioni di popolazioni che hanno la stessa varianza di popolazione. Se il campione 1 ha dimensione n1 = 5 e il campione 2 ha dimensione n2 = 10, determinare la probabilità teorica che il quoziente delle rispettive varianze sia minore o uguale a 2.
Soluzione
Va ricordato che la statistica F è definita come:
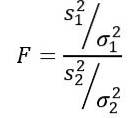
Ma ci viene detto che le varianze della popolazione sono uguali, quindi per questo esercizio si applica quanto segue:
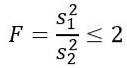
Poiché vogliamo conoscere la probabilità teorica che questo quoziente delle varianze campionarie sia minore o uguale a 2, dobbiamo conoscere l'area sotto la distribuzione F tra 0 e 2, che può essere ottenuta mediante tabelle o software. Per questo, si deve tenere conto che la distribuzione F richiesta ha d1 = n1 - 1 = 5-1 = 4 e d2 = n2 - 1 = 10-1 = 9, cioè la distribuzione F con gradi di libertà ( 4, 9).
Utilizzando lo strumento statistico di geogebra È stato determinato che quest'area è 0,82, quindi si conclude che la probabilità che il quoziente delle varianze campionarie sia inferiore o uguale a 2 è dell'82%.
Esercizio Due
Esistono due processi di produzione per fogli sottili. La variabilità dello spessore dovrebbe essere la più bassa possibile. Vengono prelevati 21 campioni da ogni processo. Il campione del processo A ha una deviazione standard di 1,96 micron, mentre il campione del processo B ha una deviazione standard di 2,13 micron. Quale dei processi ha la minore variabilità? Usa un livello di rifiuto del 5%.
Soluzione
I dati sono i seguenti: Sb = 2.13 con nb = 21; Sa = 1,96 con na = 21. Ciò significa che dobbiamo lavorare con una distribuzione F di (20, 20) gradi di libertà.
L'ipotesi nulla implica che la varianza della popolazione di entrambi i processi sia identica, cioè σa ^ 2 / σb ^ 2 = 1. L'ipotesi alternativa implicherebbe varianze della popolazione differenti.
Quindi, nell'ipotesi di varianze di popolazione identiche, la statistica F calcolata è definita come: Fc = (Sb / Sa) ^ 2.
Poiché il livello di rifiuto è stato preso come α = 0,05, allora α / 2 = 0,025
La distribuzione F (0,025, 20,20) = 0,406, mentre F (0,975, 20,20) = 2,46.
Pertanto, l'ipotesi nulla sarà vera se F calcolato soddisfa: 0.406≤Fc≤2.46. In caso contrario, l'ipotesi nulla viene respinta.
Poiché Fc = (2.13 / 1.96) ^ 2 = 1.18 si conclude che la statistica Fc è nel range di accettazione dell'ipotesi nulla con una certezza del 95%. In altre parole, con una certezza del 95%, entrambi i processi di produzione hanno la stessa varianza di popolazione..
Riferimenti
- F Test per l'indipendenza. Recupero da: saylordotorg.github.io.
- Med Wave. Statistica applicata alle scienze della salute: il test F. Estratto da: medwave.cl.
- Probabilità e statistica. Distribuzione F. Estratto da: probayestadistica.com.
- Triola, M. 2012. Statistica elementare. 11 °. Edizione. Addison Wesley.
- UNAM. Distribuzione F. Estratto da: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distribuzione F. Estratto da: es.wikipedia.com


Nessun utente ha ancora commentato questo articolo.