
Dilatazione lineare cos'è, formula e coefficienti, esempio
Il dilatazione lineare si verifica quando un oggetto subisce espansione a causa di una variazione di temperatura, prevalentemente in una dimensione. Ciò è dovuto alle caratteristiche del materiale o alla sua forma geometrica..
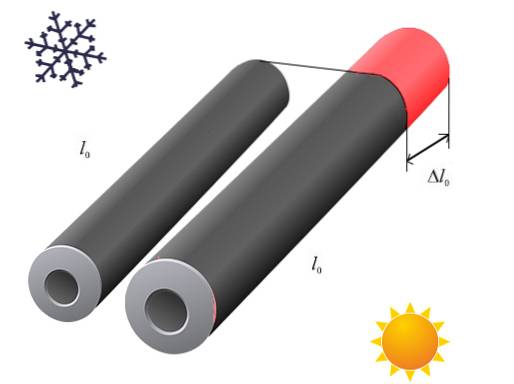
Ad esempio, in un filo o in una barra, quando c'è un aumento di temperatura, è la lunghezza che subisce la variazione maggiore a causa della dilatazione termica..

I cavi su cui si posano gli uccelli nella figura precedente subiscono un allungamento all'aumentare della loro temperatura; invece, si contraggono quando si raffreddano. Lo stesso accade, ad esempio, con le sbarre che formano i binari di una ferrovia.
Indice articolo
- 1 Cos'è la dilatazione lineare?
- 2 Formula di dilatazione lineare e suo coefficiente
- 2.1 Coefficiente di espansione lineare per vari materiali
- 3 Esempi lavorati di espansione lineare
- 3.1 Esempio 1
- 3.2 Esempio 2
- 3.3 Esempio 3
- 3.4 Esempio 4
- 4 Riferimenti
Cos'è la dilatazione lineare?
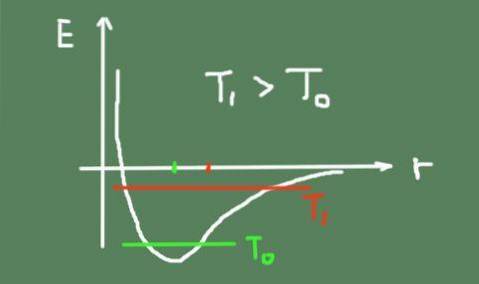
In un materiale solido, gli atomi mantengono le loro posizioni relative più o meno fisse attorno a un punto di equilibrio. Tuttavia, a causa dell'agitazione termica, oscillano sempre intorno allo stesso.
All'aumentare della temperatura, aumenta anche l'oscillazione termica, provocando il cambiamento delle posizioni di oscillazione centrale. Questo perché il potenziale di legame non è esattamente parabolico e ha un'asimmetria intorno al minimo.
Di seguito è una figura che delinea l'energia del legame chimico in funzione della distanza interatomica. Mostra anche l'energia totale di oscillazione a due temperature e come si muove il centro di oscillazione.
Formula di dilatazione lineare e suo coefficiente
Per misurare l'espansione lineare, partiamo con una lunghezza iniziale L e una temperatura iniziale T, dell'oggetto di cui misurare l'espansione..
Supponiamo che questo oggetto sia una barra la cui lunghezza è L e le dimensioni della sezione trasversale sono molto inferiori a L.
Questo oggetto viene prima sottoposto ad una variazione di temperatura ΔT, in modo che la temperatura finale dell'oggetto una volta stabilito l'equilibrio termico con la fonte di calore sarà T '= T + ΔT.
Durante questo processo, anche la lunghezza dell'oggetto sarà cambiata con un nuovo valore L '= L + ΔL, dove ΔL è la variazione della lunghezza.
Il coefficiente di dilatazione lineare α è definito come il quoziente tra la variazione relativa di lunghezza per unità di variazione di temperatura. La seguente formula definisce il coefficiente di espansione lineare α:
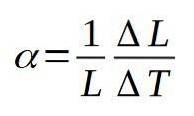
Le dimensioni del coefficiente di dilatazione lineare sono quelle dell'inverso della temperatura.
Coefficiente di espansione lineare per vari materiali
Successivamente forniremo un elenco del coefficiente di espansione lineare per alcuni materiali ed elementi tipici. Il coefficiente è calcolato alla normale pressione atmosferica sulla base di una temperatura ambiente di 25 ° C; e il suo valore è considerato costante in un intervallo di ΔT fino a 100 ° C.
L'unità del coefficiente di dilatazione lineare sarà (° C)-1.
- Acciaio: α = 12 ∙ 10-6 (° C)-1
- Alluminio: α = 23 ∙ 10-6 (° C)-1
- Oro: α = 14 ∙ 10-6 (° C)-1
- Rame: α = 17 ∙ 10-6 (° C)-1
- Ottone: α = 18 ∙ 10-6 (° C)-1
- Ferro: α = 12 ∙ 10-6 (° C)-1
- Vetro: α = (da 7 a 9) ∙ 10-6 (° C)-1
- Mercurio: α = 60,4 ∙ 10-6 (° C)-1
- Quarzo: α = 0,4 ∙ 10-6 (° C)-1
- Diamante: α = 1,2 ∙ 10-6 (° C)-1
- Piombo: α = 30 ∙ 10-6 (° C)-1
- Legno di quercia: α = 54 ∙ 10-6 (° C)-1
- PVC: α = 52 ∙ 10-6 (° C)-1
- Fibra di carbonio: α = -0,8 ∙ 10-6 (° C)-1
- Calcestruzzo: α = (da 8 a 12) ∙ 10-6 (° C)-1
La maggior parte dei materiali si allunga con un aumento della temperatura. Tuttavia, alcuni materiali speciali come la fibra di carbonio si restringono con l'aumentare della temperatura..
Esempi lavorati di dilatazione lineare
Esempio 1
Un cavo di rame è appeso tra due poli e la sua lunghezza in una giornata fresca a 20 ° C è di 12 m. Calcola il valore della sua longitudine in una giornata calda a 35 ° C.
Soluzione
Partendo dalla definizione del coefficiente di dilatazione lineare, e sapendo che per il rame tale coefficiente è pari a: α = 17 ∙ 10-6 (° C)-1
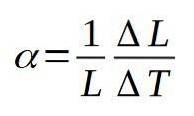
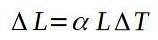
Il cavo in rame subisce un aumento della sua lunghezza, ma questa è di soli 3 mm. Cioè, il cavo va da 12.000 m ad avere 12.003 m.
Esempio 2
In una fucina, una barra di alluminio esce dal forno a 800 gradi Celsius, misurando una lunghezza di 10,00 m. Una volta che si sarà raffreddato raggiungendo la temperatura ambiente di 18 gradi Celsius, determina quanto sarà lunga la barra.
Soluzione
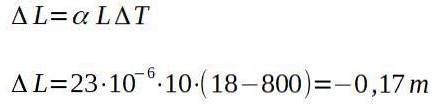
In altre parole, la barra, una volta fredda, avrà una lunghezza totale di:
9,83 m.
Esempio 3
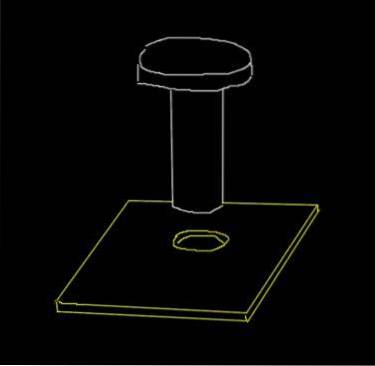
Un rivetto in acciaio ha un diametro di 0,915 cm. Su una lastra di alluminio viene praticato un foro di 0,910 cm. Questi sono i diametri iniziali quando la temperatura ambiente è di 18 ° C.
A quale temperatura minima deve essere riscaldata la piastra affinché il rivetto passi attraverso il foro? L'obiettivo di questo è che quando il ferro torna a temperatura ambiente, il rivetto sarà aderente alla piastra.
Soluzione
Sebbene la piastra sia una superficie, ci interessa la dilatazione del diametro del foro, che è una quantità unidimensionale..
Chiamiamo D0 al diametro originale della piastra di alluminio e D a cui si sarà riscaldata una volta.
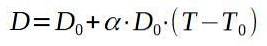
Risolvendo per la temperatura finale T, abbiamo:
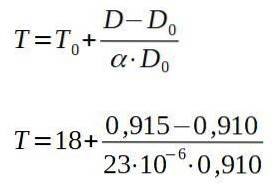
Il risultato delle operazioni precedenti è di 257 ° C, che è la temperatura minima alla quale la piastra deve essere riscaldata affinché il rivetto passi attraverso il foro.
Esempio 4
Il rivetto e la piastra dell'esercizio precedente vengono posti insieme in una fornace. Determinare a quale temperatura minima deve essere il forno affinché il rivetto in acciaio passi attraverso il foro nella piastra di alluminio.
Soluzione
In questo caso, sia il rivetto che il foro saranno dilatati. Ma il coefficiente di espansione dell'acciaio è α = 12 ∙ 10-6 (° C)-1, mentre quello dell'alluminio è α = 23 ∙ 10-6 (° C)-1 .
Cerchiamo quindi una temperatura finale T tale che entrambi i diametri coincidano.
Se chiamiamo il rivetto 1 e la piastra di alluminio 2, cerchiamo una temperatura finale T tale che D1 = DDue.
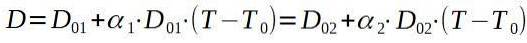
Se risolviamo la temperatura finale T, ci rimane:
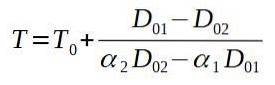
Quindi inseriamo i valori corrispondenti.
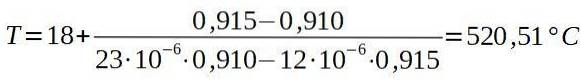
La conclusione è che il forno deve essere ad almeno 520,5 ° C affinché il rivetto possa passare attraverso il foro nella piastra di alluminio.
Riferimenti
- Giancoli, D. 2006. Fisica: principi con applicazioni. Sesta edizione. Prentice Hall. 238-249.
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mac Graw Hill. 422-527.



Nessun utente ha ancora commentato questo articolo.