
Sistema di coordinate cilindriche, cambio ed esercizi
Il coordinate cilindriche servono per localizzare punti nello spazio tridimensionale e sono costituiti da una coordinata radiale ρ, una coordinata azimutale φ e una coordinata di altezza z.
Un punto P situato nello spazio è proiettato ortogonalmente sul piano XY dando luogo al punto P ' in quell'aereo. La distanza dall'origine al punto P ' definisce la coordinata ρ, mentre l'angolo formato dall'asse X con il raggio OPERAZIONE ' definisce la coordinata φ. Infine, la coordinata z è la proiezione ortogonale del punto P sull'asse Z. (vedi figura 1).
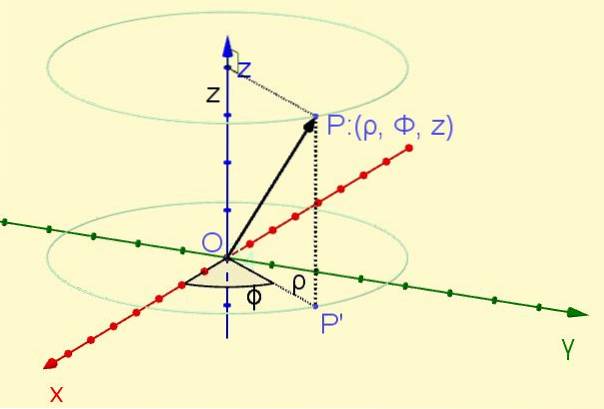
La coordinata radiale ρ è sempre positiva, la coordinata azimutale φ varia da zero radianti a due pi radianti, mentre la coordinata z può assumere qualsiasi valore reale:
0 ≤ ρ < ∞
0 ≤ φ < 2π
- ∞ < z < + ∞
Indice articolo
- 1 Cambio di coordinate
- 1.1 Base vettoriale in coordinate cilindriche
- 2 esempi
- 2.1 Esempio 1
- 2.2 Esempio 2
- 3 esercizi risolti
- 3.1 Esercizio 1
- 3.2 Esercizio 2
- 3.3 Esercizio 3
- 3.4 Esercizio 4
- 4 Riferimenti
Cambio di coordinate
È relativamente facile ottenere le coordinate cartesiane (x, y, z) di un punto P dalle sue coordinate cilindriche (ρ, φ, z):
x = ρ cos (φ)
y = ρ sin (φ)
z = z
Ma è anche possibile ricavare le coordinate polari (ρ, φ, z) partendo dalla conoscenza delle coordinate cartesiane (x, y, z) di un punto P:
ρ = √ (xDue + YDue)
φ = arctan (y / x)
z = z
Base vettoriale in coordinate cilindriche
La base dei vettori unitari cilindrici è definita Uρ, Uφ, Uz.
Il vettore Uρ è tangente alla linea φ = ctte ez = ctte (che punta radialmente verso l'esterno), il vettore Uφ è tangente alla retta ρ = ctte ez = ctte e infine Uz ha la stessa direzione dell'asse Z..
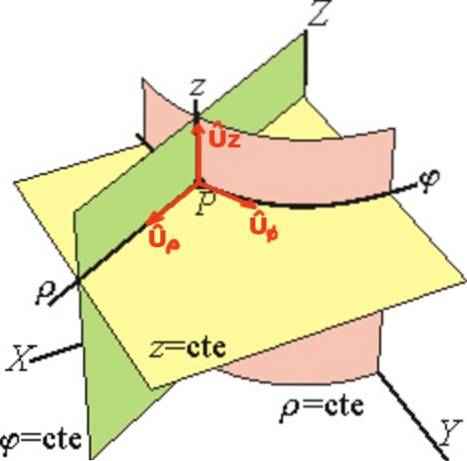
Nella base dell'unità cilindrica, il vettore di posizione r di un punto P è scritto vettorialmente così:
r = ρ Uρ + 0 Uφ + z Uz
D'altra parte, uno spostamento infinitesimale dr dal punto P si esprime come segue:
dr = dρ Uρ + ρ dφ Uφ + dz Uz
Allo stesso modo, un elemento infinitesimale di volume dV in coordinate cilindriche è:
dV = ρ dρ dφ dz
Esempi
Ci sono innumerevoli esempi di utilizzo e applicazione di coordinate cilindriche. Nella cartografia, ad esempio, il file proiezione cilindrica, basato proprio su queste coordinate. Ci sono altri esempi:
Esempio 1
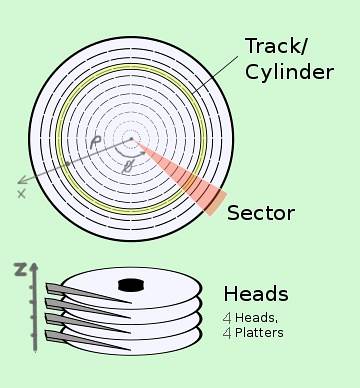
Le coordinate cilindriche hanno applicazioni nella tecnologia. Ad esempio, abbiamo il sistema CHS (Cylinder-Head-Sector) per la localizzazione dei dati su un disco rigido, che in realtà è costituito da più dischi:
- Il cilindro o la traccia corrisponde alla coordinata ρ.
- Il settore corrisponde alla posizione φ del disco che ruota in alto velocità angolare.
- La testina corrisponde alla posizione z della testina di lettura sul disco corrispondente.
Ogni byte di informazione ha un indirizzo preciso in coordinate cilindriche (C, S, H).
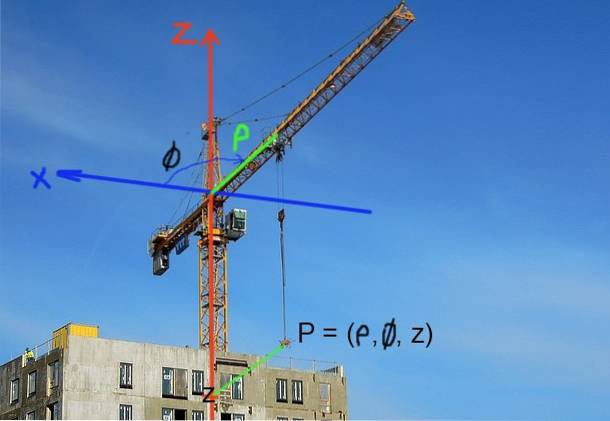
Esempio 2
Le gru edili fissano la posizione del carico in coordinate cilindriche. La posizione orizzontale è definita dalla distanza dall'asse o freccia della gru ρ e dalla sua posizione angolare φ rispetto a qualche asse di riferimento. La posizione verticale del carico è determinata dalla coordinata z dell'altezza.
Esercizi risolti
Esercizio 1
Ci sono punti P1 con coordinate cilindriche (3, 120º, -4) e punto P2 con coordinate cilindriche (2, 90º, 5). Trovare la Distanza euclidea tra questi due punti.
Soluzione: Per prima cosa, procediamo per trovare le coordinate cartesiane di ogni punto seguendo la formula data sopra.
P1 = (3 * cos 120º, 3 * sin 120º, -4) = (-1.5, 2.60, -4)
P2 = (2 * cos 90º, 2 * sin 90º, 5) = (0, 2, 5)
La distanza euclidea tra P1 e P2 è:
d (P1, P2) = √ ((0 - (-1,5))Due+(2 - 2.60)Due+(5 - (- 4))Due ) = ...
… √ (2,25 + 0,36 + 81) = 9,14
Esercizio 2
Il punto P ha coordinate cartesiane (-3, 4, 2). Trova le coordinate cilindriche corrispondenti.
Soluzione: Procediamo per trovare le coordinate cilindriche utilizzando le relazioni sopra riportate:
ρ = √ (xDue + YDue) = √ ((- 3)Due + 4Due) = √ (9 + 16) = √ (25) = 5
φ = arctan (y / x) = arctan (4 / (- 3)) = -53,13º + 180º = 126,87º
z = 2
Va ricordato che la funzione arcotangente è multivalore con periodicità di 180º. Inoltre, l'angolo φ deve appartenere al secondo quadrante, poiché le coordinate xey del punto P si trovano in quel quadrante. Questo è il motivo per cui 180º è stato aggiunto al risultato φ.
Esercizio 3
Esprimere in coordinate cilindriche e in coordinate cartesiane la superficie di un cilindro di raggio 2 e il cui asse coincide con l'asse Z.
Soluzione: Resta inteso che il cilindro ha un'estensione infinita nella direzione z, quindi l'equazione di detta superficie in coordinate cilindriche è:
ρ = 2
Per ottenere l'equazione cartesiana della superficie cilindrica, si prende il quadrato di entrambi i membri dell'equazione precedente:
ρDue = 4
Moltiplichiamo per 1 entrambi i membri dell'uguaglianza precedente e applichiamo il identità trigonometrica fondamentale (senDue(φ) + cosDue(φ) = 1):
1 * ρDue = 1 * 4
(senDue(φ) + cosDue(φ)) * ρDue = 1 * 4
La parentesi si sviluppa per ottenere:
(ρ sin (φ))Due + (ρ cos (φ))Due = 4
Ricordiamo che la prima parentesi (ρ sin (φ)) è la coordinata y di un punto in coordinate polari, mentre le parentesi (ρ cos (φ)) rappresenta la coordinata x, quindi abbiamo l'equazione del cilindro in coordinate cartesiane:
YDue + XDue = 2Due
L'equazione precedente non deve essere confusa con quella di un cerchio nel piano XY, poiché in questo caso sarebbe simile a questa: yDue + XDue = 2Due ; z = 0.
Esercizio 4
Un cilindro di raggio R = 1 me altezza H = 1 m ha la sua massa distribuita radialmente secondo la seguente equazione D (ρ) = C (1 - ρ / R) dove C è una costante di valore C = 1 kg / m3. Trova la massa totale del cilindro in chilogrammi.
Soluzione: La prima cosa è rendersi conto che la funzione D (ρ) rappresenta la densità di massa volumetrica e che la densità di massa è distribuita in gusci cilindrici di densità decrescente dal centro alla periferia. Un elemento infinitesimale di volume secondo la simmetria del problema è:
dV = ρ dρ 2π H
Quindi, la massa infinitesimale di un guscio cilindrico sarà:
dM = D (ρ) dV
Pertanto, la massa totale del cilindro sarà espressa come segue integrale definito:
M = ∫oR D (ρ) dV = ∫oR C (1 - ρ / R) ρ dρ 2π H = 2π H C ∫oR (1 - ρ / R) ρ dρ
La soluzione dell'integrale indicato non è difficile da ottenere, il suo risultato è:
∫oR (1 - ρ / R) ρ dρ = (⅙) RDue
Incorporando questo risultato nell'espressione della massa del cilindro, si ottiene:
M = 2π H C (⅙) RDue = ⅓ π H C RDue =
⅓ π 1 m * 1 kg / m3* 1 mDue = π / 3 kg ≈ 1,05 kg
Riferimenti
- Arfken G e Weber H. (2012). Metodi matematici per fisici. Una guida completa. 7a edizione. Stampa accademica. ISBN 978-0-12-384654-9
- Calcolo cc. Risolti problemi di coordinate cilindriche e sferiche. Estratto da: calculo.cc
- Weisstein, Eric W. "coordinate cilindriche". Da MathWorld-A Wolfram Web. Estratto da: mathworld.wolfram.com
- wikipedia. Sistema di coordinate cilindrico. Estratto da: en.wikipedia.com
- wikipedia. Campi vettoriali in coordinate cilindriche e sferiche. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.