Il Costante di Boltzmann è il valore che mette in relazione l'energia cinetica media di un sistema termodinamico o di un oggetto con la sua temperatura assoluta. Sebbene siano spesso confusi, temperatura ed energia non sono lo stesso concetto.
La temperatura è una misura dell'energia, ma non l'energia stessa. Con la costante di Boltzmann, sono collegati tra loro nel modo seguente:
Ec = (3/2) kB T
Questa equazione è valida per una molecola di gas ideale monoatomico di massa m, dove Ec è la sua energia cinetica espressa in Joules, kB è la costante di Boltzmann e T è la temperatura assoluta in Kelvin.
In questo modo, all'aumentare della temperatura, aumenta anche l'energia cinetica media per molecola di sostanza, come previsto. E il contrario accade quando la temperatura diminuisce, potendo raggiungere il punto in cui se tutto il movimento cessa, si raggiunge la temperatura più bassa possibile o lo zero assoluto..
Quando si parla di energia cinetica media, è necessario ricordare che l'energia cinetica è associata al movimento. E le particelle possono muoversi in molti modi, come muoversi, ruotare o vibrare. Naturalmente, non tutti lo faranno allo stesso modo, e poiché sono innumerevoli, viene presa la media per caratterizzare il sistema..
Alcuni stati energetici sono più probabili di altri. Questo concetto è di fondamentale importanza nella termodinamica. L'energia considerata nell'equazione precedente è l'energia cinetica traslazionale. La probabilità degli stati e la sua relazione con la costante di Boltzmann verrà discussa più avanti..
Nel 2018 è stato ridefinito il Kelvin e con esso la costante di Boltzmann, che nel Sistema Internazionale è di circa 1.380649 x 10-2. 3 J. K-1. È possibile ottenere una precisione molto maggiore per la costante di Boltzmann, che è stata determinata in numerosi laboratori in tutto il mondo, con metodi diversi..
Indice articolo
La famosa costante deve il suo nome al fisico viennese Ludwig Boltzmann (1844-1906), che dedicò la sua vita di scienziato allo studio del comportamento statistico di sistemi con molte particelle, dal punto di vista della meccanica newtoniana..
Sebbene oggi l'esistenza dell'atomo sia universalmente accettata, nel diciannovesimo secolo la convinzione se l'atomo esistesse davvero o fosse un artificio con cui venivano spiegati molti fenomeni fisici era in pieno dibattito..
Boltzmann era un convinto difensore dell'esistenza dell'atomo e ai suoi tempi dovette affrontare aspre critiche al suo lavoro da parte di molti colleghi, che ritenevano che contenesse paradossi insolubili..
Ha affermato che i fenomeni osservabili a livelli macroscopici potrebbero essere spiegati dalle proprietà statistiche delle particelle costituenti come atomi e molecole..
Forse queste critiche furono dovute al profondo episodio di depressione che lo portò a togliersi la vita all'inizio di settembre 1906, quando aveva ancora molto da fare, visto che era considerato uno dei grandi fisici teorici del suo tempo e c'era resta molto poco da fare che altri scienziati contribuiscano a corroborare la veridicità delle loro teorie.
Non passò molto tempo dopo la sua morte che nuove scoperte sulla natura dell'atomo e delle sue particelle costituenti si sommarono per dimostrare che Boltzmann aveva ragione..
Ora, la costante di Boltzmann KB fu introdotto come è noto oggi qualche tempo dopo i lavori del fisico austriaco. Fu Max Planck, nella sua legge dell'emissione del corpo nero, opera che presentò nel 1901, che in quel momento le diede il valore di 1,34 x 10−23 J / K.
Intorno al 1933 una targa con la definizione di entropia che coinvolge la famosa costante fu aggiunta alla lapide di Boltzmann a Vienna come tributo postumo: S = kB log W, equazione che verrà discussa più avanti.
Oggi la costante di Boltzmann è indispensabile nell'applicazione delle leggi della termodinamica, della meccanica statistica e della teoria dell'informazione, campi di cui questo triste fisico è stato un pioniere..
I gas possono essere descritti in termini macroscopici e anche in termini microscopici. Per la prima descrizione ci sono concetti come densità, temperatura e pressione.
Tuttavia, va ricordato che un gas è composto da molte particelle, che hanno una tendenza globale a un certo comportamento. È questa tendenza che viene misurata macroscopicamente. Un modo per determinare la costante di Boltzmann è grazie alla ben nota equazione dei gas ideali:
p.V = n. R. T
Qui p è la pressione del gas, V è il suo volume, n è il numero di moli presenti, R è la costante dei gas e T è la temperatura. In una mole di gas ideale, la seguente relazione è soddisfatta tra il prodotto p.V, e l'energia cinetica traslazionale K l'intero set è:
p.V = (2/3). K
Pertanto l'energia cinetica è:
K = (3/2) n.R.T
Dividendo per il numero totale di molecole presenti, che si chiamerà N, si ottiene l'energia cinetica media di una singola particella:
Ec = K / N
Ec= (3 / 2N) n.R.T
In una talpa c'è il numero di particelle N di AvogadroPER, e quindi il numero totale di particelle è N = nNA, rimanendo:
Ec = (3 / 2nNPER) n.R.T
Proprio il quoziente R / NPER è la costante di Boltzmann, dimostrando così che l'energia cinetica traslazionale media di una particella dipende solo dalla temperatura assoluta T e non da altre grandezze come la pressione, il volume o anche il tipo di molecola:
Ec = (3/2) kB. T
Un gas ha una data temperatura, ma quella temperatura può corrispondere a diversi stati di energia interna. Come visualizzare questa differenza?
Considera il lancio simultaneo di 4 monete e il modo in cui possono cadere:
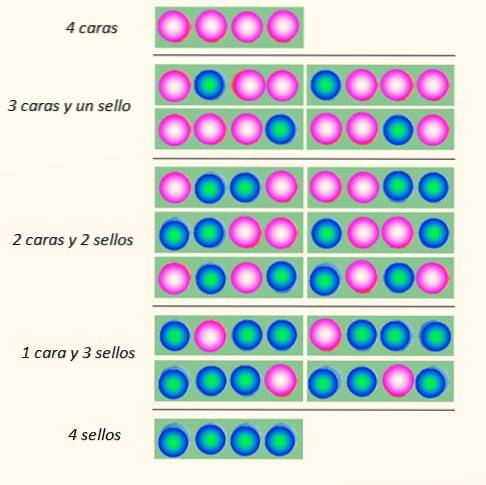
Il set di monete può assumere un totale di 5 stati, che vengono considerati macroscopico, descritto in figura. Quale di questi stati direbbe il lettore è il più probabile?
La risposta dovrebbe essere lo stato di 2 teste e 2 croci, perché hai un totale di 6 possibilità, delle 16 illustrate in figura. E 24 = 16. Questi sono equivalenti agli stati microscopico.
Cosa succede se vengono lanciate 20 monete invece di 4? Ci sarebbe un totale di 2venti possibilità o "stati microscopici". È un numero molto più grande e più difficile da gestire. Per facilitare la gestione di grandi numeri, i logaritmi sono molto appropriati.
Quello che sembra evidente è che lo stato con il maggior disordine è il più probabile. Stati più ordinati come 4 teste o 4 sigilli sono leggermente meno probabili.
L'entropia di uno stato macroscopico S è definita come:
S = kB ln w
Dove w è il numero di possibili stati microscopici del sistema e KB è la costante di Boltzmann. Che cosa ln w è adimensionale, l'entropia ha le stesse unità di kB: Joule / K.
Questa è la famosa equazione sulla lapide di Boltzmann a Vienna. Tuttavia, più che l'entropia, ciò che è rilevante è il suo cambiamento:
ΔS = kB ln wDue - KB ln w1 = kB ln (wDue/ w1)
Il valore della costante di Boltzmann è ottenuto sperimentalmente con estrema precisione con misure basate su termometria acustica, che vengono eseguiti utilizzando la proprietà che stabilisce la dipendenza della velocità del suono in un gas con la sua temperatura.
Infatti, la velocità del suono in un gas è data da:
Badiabatico = γp
E ρ è la densità del gas. Per l'equazione di cui sopra, p è la pressione del gas in questione e γ è il coefficiente adiabatico, il cui valore per un dato gas si trova nelle tabelle.
Gli istituti di metrologia stanno anche sperimentando altri modi per misurare la costante, come il Termometria del rumore Johnson, che utilizza le fluttuazioni termiche che si verificano casualmente nei materiali, in particolare nei conduttori.
Trova:
a) Energia cinetica traslazionale media Ec che ha una molecola di gas ideale a 25 ºC
b) Energia cinetica traslazionale K delle molecole in 1 mole di questo gas
c) La velocità media di una molecola di ossigeno a 25 ºC
mossigeno = 16 x 10 -3 kg / mol
per) Ec = (3/2) k T = 1,5 x 1.380649 x 10-2. 3J. K-1 x 298 K = 6,2 x 10-ventuno J
b) K = (3/2) n.R.T = 5 x 1 mol x 8,314 J / mol. K x 298 K = 3716 J
c) Ec = ½ mvDue, tenendo conto che la molecola di ossigeno è biatomica e la massa molare va moltiplicata per 2, avremo:
Trova la variazione di entropia quando 1 mole di gas occupa un volume di 0,5 m3 si espande per occupare 1 m3.
ΔS = kB ln (wDue/ w1)
wDue= 2Nw1 (C'erano 24 stati microscopici per il lancio delle 4 monete, ricordi?)
Dove N è il numero di particelle presenti in 0,5 moli di gas 0,5 x NPER:
ΔS = kB ln (2N w1/ w1) = kB ln 2N= kB 0,5 N.PER ln 2 = 2,88 J / K
Nessun utente ha ancora commentato questo articolo.