
Conservazione del principio della quantità di moto lineare, esempi, esercizi.
Il conservazione della quantità di moto lineare di un corpo stabilisce che il prodotto della sua massa e del suo vettore di velocità è una quantità costante, quando il corpo è libero da interazioni con altri corpi e con la velocità misurata rispetto ad un sistema di riferimento fisso o non accelerato.
Quando hai più corpi che interagiscono solo tra loro, ma non con l'ambiente esterno, allora il file momento lineare del set inoltre rimane costante nel tempo.

La quantità di moto lineare, la quantità di moto o semplicemente il quantità di moto, è indicato dalla lettera p y è una quantità vettoriale:
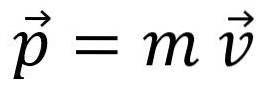
Lo slancio non è lo stesso della velocità, anche se la relazione è ovvia: ad esempio, un camion che va a 20 km / h ha più slancio di una bicicletta che si muove alla stessa velocità.
Perché la quantità di moto lineare di un corpo cambi, una forza esterna netta deve agire su di esso, altrimenti rimane costante. Inoltre, il momento lineare P di un sistema formato da n-corpi è la somma vettoriale dei singoli momenti:
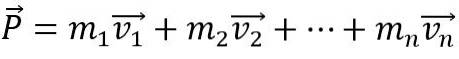
Indice articolo
- 1 Principio di conservazione della quantità di moto lineare
- 2 esempi
- 2.1 Esempio 1
- 2.2 Esempio 2
- 2.3 Esempio 3
- 3 Applicazioni
- 3.1 Nave nello spazio
- 3.2 Vita quotidiana
- 4 esercizi
- 4.1 Esercizio 1
- 4.2 Esercizio 2
- 5 Riferimenti
Principio di conservazione della quantità di moto lineare
In un corpo privo di forze (o in cui tutte le forze su di esso si annullano) accade che il momento lineare rimanga costante.
Lo stesso accade in un sistema formato da più corpi che interagiscono solo tra loro, ma non con l'ambiente esterno: la quantità di moto lineare totale del sistema rimane fissa durante l'evoluzione del movimento dell'insieme..
Questo principio di conservazione è affermato come segue:
La quantità di moto totale di un insieme di n-corpi che interagiscono solo tra loro, ma non con l'ambiente esterno, è una quantità invariabile nel tempo.
E matematicamente si esprime come segue:
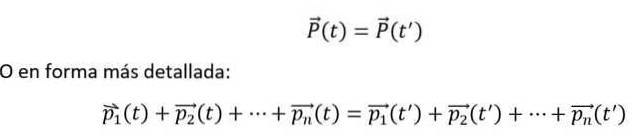
Le uguaglianze di cui sopra sono soddisfatte, se e solo se il n-i corpi interagiscono tra loro, ma non con l'ambiente esterno. Inoltre, i singoli momenti devono sempre essere misurati rispetto a un sistema di riferimento inerziale..
Esempi
Esempio 1

Due astronauti nello spazio si tengono per mano e sono tenuti in una posizione fissa rispetto al veicolo spaziale. Ma se si spingono a vicenda, iniziano a separarsi in direzioni opposte, se visti dalla nave..
In questo caso, poiché l'interazione tra gli astronauti avviene solo tra di loro attraverso la forza di contatto delle loro mani, lo slancio totale dopo la spinta è ancora il valore iniziale rispetto alla navicella. Cioè, quantità di moto totale 0.
Tuttavia, lo slancio di ogni astronauta è cambiato. Inizialmente ognuno aveva 0 momento lineare rispetto alla nave, ma dopo essere stato spinto, uno esce in una direzione e l'altro nella direzione opposta, con momenti lineari diversi da zero di uguale grandezza e direzioni opposte..
Pertanto, quando i singoli momenti vengono sommati vettorialmente, si ottiene come risultato la quantità di moto totale iniziale, che è zero.
D'altra parte, la conservazione della quantità di quantità di moto indica che l'astronauta con la massa più bassa è quello che si muove più velocemente rispetto alla navicella. Ma il risultato di moltiplicare la sua massa per la sua velocità è uguale al prodotto ottenuto moltiplicando la massa dell'altro per la velocità dell'altro.
Esempio 2
Un cucciolo è su una piattaforma galleggiante in un lago calmo e il suo padrone lo osserva da un molo. All'inizio sia la piattaforma che il cucciolo sono a riposo, ma quando il cucciolo vuole avvicinarsi al proprietario, la piattaforma si allontana dalla banchina.
La spiegazione di questa osservazione sta proprio nel principio di conservazione della quantità di quantità di moto lineare. Il sistema è composto dal cucciolo e dalla piattaforma.
Il cucciolo può camminare sulla piattaforma grazie alla forza di attrito tra le sue gambe e la superficie, in questo caso la forza di attrito è una forza interna di interazione tra esso e la piattaforma.
Il tutto è un sistema isolato, poiché la piattaforma può muoversi orizzontalmente sul lago, priva di qualsiasi resistenza al movimento. D'altra parte, nella direzione verticale tutte le forze sono bilanciate e compensate, e il tutto non ha movimento in quella direzione..
Pertanto, in questa situazione tutte le ipotesi sono soddisfatte in modo che si applichi il principio di conservazione della quantità di moto lineare.
Esempio 3

Un eschimese è intrappolato al centro di un lago ghiacciato, il ghiaccio è così liscio che per quanto ci provi, l'eschimese scivola e rimane sempre nello stesso posto.
L'unico modo possibile per l'eschimese di uscire dal lago è per lui di lanciare nella direzione opposta a quella in cui vuole spostare un oggetto pesante che porta nello zaino (ammesso che ne porti uno).
Applicazioni
Nave nello spazio

La conservazione della quantità di moto lineare viene applicata per spingere un razzo nello spazio esterno dove non ci sono forze esterne. In questo caso, l'impulso della nave si ottiene espellendo i gas ad alta velocità, in modo che il razzo possa muoversi nella direzione opposta a quella in cui sono stati espulsi..
Se originariamente la nave è a riposo, quando brucia ed espelle carburante, la forza di espulsione si verifica contro la nave stessa. È una forza interna tra i gas e la nave. Non ci sono forze esterne e quindi si applica la conservazione della quantità di moto lineare.
Poiché la quantità di moto lineare dei gas è uguale e opposta a quella della nave, riesce a uscire dallo stato di riposo, e continuando ad espellere i gas, aumenta la sua quantità di movimento e quindi la sua velocità.
Vita quotidiana

Un altro caso di applicazione della conservazione della quantità di moto lineare nella vita di tutti i giorni è piantare un chiodo nel legno, sfruttando la quantità di movimento o quantità di moto del martello..
Si potrebbe sostenere che in questo caso il principio non si applica, perché c'è una forza esterna: la resistenza che il legno offre al chiodo..
Tuttavia, al momento del contatto, la forza che il martello impone al chiodo è una forza interna (tra il sistema che è il chiodo e il martello) molto maggiore della resistenza che oppone il legno, e quindi quest'ultima è trascurabile.
Tutto lo slancio del martello, che è abbastanza grande a causa della sua grande massa e velocità, viene trasferito al chiodo subito dopo la collisione. Si noti che tutto il momento, ma non tutta l'energia cinetica del martello viene trasferita, poiché parte di questa viene trasformata in energia termica nel chiodo e nel martello, che aumentano la loro temperatura dopo l'impatto.
Formazione
Esercizio 1
Gli astronauti Andrew e Berenice sono fuori dalla stazione spaziale, si tengono entrambe le mani e sono a riposo rispetto alla stazione. Vengono spinti spingendo le mani l'uno contro l'altro e vengono rilasciati. Se Andrea, 70 kg di massa, si muove a 1 m / s rispetto alla stazione, qual è la velocità di Berenice con 49 kg di massa?
Soluzione
In questo caso, le ipotesi di conservazione della quantità di moto lineare si applicano chiaramente, poiché non ci sono forze esterne nello spazio esterno. La forza con cui entrambi gli astronauti spingono le mani è una forza interna.
Supponiamo che la massa di Andrew sia Mper e quella di Berenice Mb. Allo stesso modo, le velocità di entrambi dopo l'impulso sono Vper per Andrew e Vb per Berenice. Quindi la conservazione della quantità di moto lineare si applica in questo modo:
Mper∙0 + Mb∙0 = Mper∙Vper+ Mb∙Vb
Risolvendo per la velocità di Berenice abbiamo:
Vb = - (Mper / Mb) ∙ Vper
Posizionamento dei valori numerici:
Vb = - (70/49) ∙ (1 m / s) o = -1,43 m / s o
Cioè Berenice si muove con una velocità di 1,43 m / s in direzione opposta a quella di Andrea.
Esercizio 2

Un cucciolo di massa 5 kg è a riposo su una piattaforma di 15 kg che galleggia, anche a riposo, su un lago fermo. Se il cucciolo inizia a camminare sulla piattaforma ad una velocità di 0,5 m / s rispetto ad essa. Quanto saranno veloci il cucciolo e la pedana rispetto ad un osservatore fissato a terra??
Soluzione
Il sistema di riferimento inerziale sarà preso come molo dove si trova il proprietario del cucciolo. Inizialmente sia il cucciolo che la piattaforma galleggiante sono a riposo rispetto alla banchina..
Quando il cucciolo decide di camminare velocemente verso il proprietario v ' rispetto alla piattaforma, la piattaforma si allontana dal molo con velocità +V. La velocità del cucciolo rispetto alla molla si ottiene per mezzo della somma vettoriale della sua velocità rispetto alla pedana più la velocità della pedana e la denotiamo con:
v = -v' + V
Poiché la resistenza dell'acqua al movimento della piattaforma è praticamente nulla a causa della sua bassa velocità, allora si può affermare che il sistema composto da il cucciolo + la piattaforma è un sistema isolato e si applica il principio di conservazione della quantità di moto lineare:
0 = m ∙ v + M ∙ V
Ricordando che v = v '+ V abbiamo:
0 = -m ∙ v '+ m ∙ v + M ∙ V
Ovvero: m ∙ v '= (m + M) ∙ V
Quindi V = [m / (m + M)] v 'e v = - (M / m) V = - [M / (m + M)] v'
Sostituendo i valori numerici abbiamo:
V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s
Questa è la velocità con cui la piattaforma si allontana dal molo.
V = - (15/20) ∙ 0,5 m / s = -0,375 m / s
E questa è la velocità con cui il cucciolo si avvicina al molo.
Riferimenti
- Duke University. Sistemi di particelle. Recupero da: webhome.phy.duke.edu.
- Rex, A. 2011. Fondamenti di fisica. Pearson.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.
- .


Welcome to the world of adult Dating loveawake.ru