Shock elastici in una dimensione, casi speciali, esercizi

Il urti elastici o le collisioni elastiche consistono in interazioni brevi ma intense tra oggetti, in cui vengono conservate sia la quantità di moto che l'energia cinetica. Gli incidenti sono eventi molto frequenti in natura: dalle particelle subatomiche alle galassie, alle palle da biliardo e agli autoscontri nei parchi di divertimento, sono tutti oggetti in grado di scontrarsi.

Durante una collisione o una collisione, le forze di interazione tra gli oggetti sono molto forti, molto più di quelle che possono agire esternamente. In questo modo si può affermare che durante l'urto le particelle formano un sistema isolato.

In questo caso è vero che:

P_o = P_F

La quantità di movimento P_o prima della collisione è la stessa che dopo la collisione. Questo vale per qualsiasi tipo di collisione, sia elastica che anelastica..

Consideriamo ora quanto segue: durante una collisione gli oggetti subiscono una certa deformazione. Quando l'ammortizzatore è elastico, gli oggetti riacquistano rapidamente la loro forma originale.

Indice articolo

• 1 Conservazione dell'energia cinetica
• 2 ammortizzatori elastici in una dimensione
  • 2.1 -Formule per urti elastici
• 3 Casi speciali in urti elastici
  • 3.1 Due masse identiche
  • 3.2 Due masse identiche, di cui una inizialmente a riposo
  • 3.3 Due masse differenti, una delle quali inizialmente a riposo
• 4 Coefficiente di restituzione o regola di Huygens-Newton
• 5 Esercizi risolti
  • 5.1 -Esercizio risolto 1
  • 5.2 -Esercizio risolto 2
  • 5.3 -Esercizio risolto 3
  • 5.4 -Esercizio risolto 4
• 6 Riferimenti

Conservazione dell'energia cinetica

Normalmente durante un incidente, parte dell'energia degli oggetti viene spesa per il calore, la deformazione, il suono e talvolta anche per la produzione di luce. Quindi l'energia cinetica del sistema dopo la collisione è inferiore all'energia cinetica originale.

Quando l'energia cinetica K è conservata allora:

K_o = K_F

Ciò significa che le forze che agiscono durante la collisione sono conservative. Durante la collisione l'energia cinetica viene brevemente trasformata in energia potenziale e poi di nuovo in energia cinetica. Le rispettive energie cinetiche variano, ma la somma rimane costante.

Le collisioni perfettamente elastiche sono rare, sebbene le palle da biliardo siano un'approssimazione abbastanza buona, così come le collisioni che si verificano tra le molecole di gas ideali..

Ammortizzatori elastici in una dimensione

Esaminiamo una collisione di due particelle di questo in una singola dimensione; cioè, le particelle interagenti si muovono, diciamo, lungo l'asse x. Supponiamo che abbiano delle masse m₁ Y m_Due. Le velocità iniziali di ciascuna sono o₁ Y o_Due rispettivamente. Le velocità finali sono v₁ Y v_Due.

Possiamo fare a meno della notazione vettoriale, poiché il movimento viene effettuato lungo l'asse x, tuttavia i segni (-) e (+) indicano la direzione del movimento. A sinistra è negativo e a destra positivo, per convenzione.

-Formule per collisioni elastiche

Per la quantità di movimento

m₁o₁ + m_Dueo_Due = m₁v₁ + m_Duev_Due

Per l'energia cinetica

½ m₁o^Due₁ + ½ m_Dueo^Due_Due = ½ m₁v^Due₁ +  ½ m_Duev^Due_Due

A condizione che le masse e le velocità iniziali siano note, le equazioni possono essere raggruppate per trovare le velocità finali.

Il problema è che in linea di principio è necessario eseguire un'algebra un po 'noiosa, poiché le equazioni per l'energia cinetica contengono i quadrati delle velocità, il che rende il calcolo un po' macchinoso. L'ideale sarebbe trovare espressioni che non le contengano.

La prima cosa è fare a meno del fattore ½ e riorganizzare entrambe le equazioni in modo che appaia un segno negativo e si possano fattorizzare le masse:

m₁o₁ - m₁v₁ = M_Duev_Due - m_Dueo_Due

m₁o^Due₁ - m₁v^Due₁  = + M_Duev^Due_Due - m_Dueo^Due_Due

Essendo espresso in questo modo:

m₁(o₁ - v₁ ) = m_Due(v_Due - o_Due)

m₁(o^Due₁ - v^Due₁ ) = m_Due (v^Due_Due - o^Due_Due)

Semplificazione per eliminare i quadrati delle velocità

Ora dobbiamo utilizzare il prodotto somma notevole per la sua differenza nella seconda equazione, con la quale otteniamo un'espressione che non contiene i quadrati, come originariamente voluto:

m₁(o₁ - v₁ ) = m_Due(v_Due - o_Due)

m₁(o₁ - v₁ ) (o₁ + v₁ ) = m_Due (v_Due - o_Due) (v_Due + o_Due)

Il prossimo passo è sostituire la prima equazione nella seconda:

m_Due(v_Due - o_Due) (o₁ + v₁ ) = m_Due (v_Due - o_Due) (v_Due + o_Due)

E quando il termine si ripete m_Due(v_Due - o_Due) su entrambi i lati dell'uguaglianza, detto termine è annullato e si presenta così:

(o₁ + v₁) = (v_Due + o_Due)

O ancora meglio:

o₁ - o_Due= v_Due -  v₁

Velocità finali v₁ e V_Due delle particelle

Ora hai due equazioni lineari con cui è più facile lavorare. Li rimetteremo uno sotto l'altro:

m₁o₁ + m_Dueo_Due = m₁v₁ + m_Duev_Due

o₁ - o_Due= v_Due -  v₁

Moltiplicando la seconda equazione per m₁ e l'aggiunta di un termine al termine è:

m₁o₁ + m_Dueo_Due = m₁v₁ + m_Duev_Due

m₁o₁ - m₁o_Due= m₁v_Due - m₁ v₁

-

2 m₁o₁ + (m_Due - m₁) o_Due = (m_Due + m₁) v_Due

Ed è già possibile cancellare v_Due. Per esempio:

Casi speciali in urti elastici

Ora che le equazioni sono disponibili per le velocità finali di entrambe le particelle, è il momento di analizzare alcune situazioni speciali.

Due masse identiche

Poi m₁ = m_Due = m Y:

v₁ = u_Due

v_Due = u₁

Le particelle semplicemente scambiano le loro velocità dopo la collisione.

Due masse identiche, di cui una inizialmente a riposo

Ancora  m₁ = m_Due = m e supponendo che o₁ = 0:

v₁ = u_Due

v_Due = 0

Dopo la collisione, la particella che era a riposo acquisisce la stessa velocità della particella che si stava muovendo, e questa a sua volta si ferma.

Due messe diverse, una delle quali inizialmente a riposo

In questo caso supponiamo che o₁ = 0, ma le masse sono diverse:

Cosa succede se m₁ è molto maggiore di m_Due?

Succede che m₁ è ancora a riposo e m_Due ritorna velocemente come viene colpito.

Coefficiente di restituzione o regola di Huygens-Newton

In precedenza, la seguente relazione tra le velocità era derivata per due oggetti in collisione elastica: o₁ - o_Due = v_Due -  v₁. Queste differenze sono le velocità relative prima e dopo la collisione. In generale, per una collisione è vero che:

o₁ - o_Due = - (v₁ -  v_Due)

Il concetto di velocità relativa si apprezza meglio se il lettore immagina di essere su una delle particelle e da questa posizione osserva la velocità con cui si muove l'altra particella. L'equazione di cui sopra viene riscritta in questo modo:

Esercizi risolti

-Risolto esercizio 1

Una palla da biliardo si muove a sinistra a 30 cm / s, scontrandosi frontalmente con un'altra palla identica che si muove a destra a 20 cm / s. Le due sfere hanno la stessa massa e l'urto è perfettamente elastico. Trovare la velocità di ogni palla dopo l'impatto.

Soluzione

o₁ = -30 cm / s

o_Due = +20 cm / s

È il caso speciale in cui due masse identiche entrano in collisione elasticamente in una dimensione, quindi le velocità vengono scambiate.

v₁ = +20 cm / s

v_Due = -30 cm / s

-Esercizio risolto 2

Il coefficiente di restituzione di una palla che rimbalza da terra è pari a 0,82. Se cade da fermo, quale frazione della sua altezza originale raggiungerà la palla dopo aver rimbalzato una volta? E dopo 3 rimbalzi?

Soluzione

Il suolo può essere l'oggetto 1 nell'equazione del coefficiente di restituzione. E rimane sempre a riposo, in modo che:

Con questa velocità rimbalza:

Il segno + indica che si tratta di una velocità ascendente. E secondo esso, la palla raggiunge un'altezza massima di:

Ora ritorna di nuovo a terra con una velocità della stessa grandezza, ma segno opposto:

Questo raggiunge un'altezza massima di:

Torna a terra con:

Rimbalzi successivi

Ogni volta che la pallina rimbalza e si alza, moltiplica di nuovo la velocità per 0,82:

Ormai h₃ è circa il 30% di h_o. Quale sarebbe l'altezza del 6 ° rimbalzo senza la necessità di fare calcoli così dettagliati come i precedenti?

Voluto h₆ = 0,82¹² h_o = 0,092 h_o o solo il 9% di h_o.

-Esercizio risolto 3

Un blocco da 300 g si muove verso nord a 50 cm / se si scontra con un blocco da 200 g che si dirige a sud a 100 cm / s. Supponiamo che l'ammortizzatore sia perfettamente elastico. Trova le velocità dopo l'impatto.

Dati

m₁ = 300 g; o₁ = + 50 cm / s

m_Due = 200 g; o_Due = -100 cm / s

-Esercizio risolto 4

Viene rilasciata una massa di m₁ = 4 kg dal punto indicato sulla pista priva di attrito, fino a che non entra in collisione con m_Due = 10 kg a riposo. Quanto in alto si alza?₁ dopo la collisione?

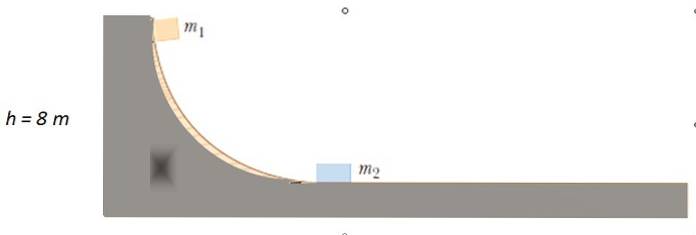
Soluzione

Poiché non c'è attrito, l'energia meccanica viene conservata per trovare la velocità o₁ con Cosa m₁ impatti  m_Due. Inizialmente l'energia cinetica è 0, da allora m₁ parte del riposo. Quando si muove sulla superficie orizzontale non ha altezza, quindi l'energia potenziale è 0.

mgh = ½ mu₁ ^Due

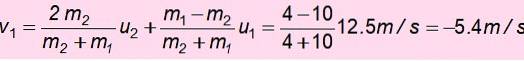
o_Due = 0

Ora la velocità di m₁ dopo la collisione:

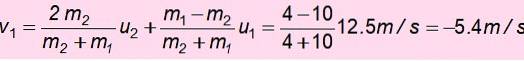
Il segno negativo significa che è stato restituito. Con questa velocità sale e l'energia meccanica viene nuovamente conservata per ritrovarla h ', l'altezza alla quale puoi salire dopo lo schianto:

½ mv₁^Due = mgh '

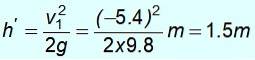
Si noti che non ritorna al punto di partenza a un'altitudine di 8 m. Non ha abbastanza energia perché la massa ha dato parte della sua energia cinetica m_1.

Riferimenti

1. Giancoli, D. 2006. Fisica: principi con applicazioni. 6^th. Ed Prentice Hall. 175-181
2. Rex, A. 2011. Fondamenti di fisica. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Fondamenti di fisica. 9^{n / A} Cengage Learning. 172-182
4. Tipler, P. (2006) Physics for Science and Technology. 5a Ed. Volume 1. Editoriale Reverté. 217-238
5. Tippens, P. 2011. Fisica: concetti e applicazioni. 7a edizione. MacGraw Hill. 185-195