
Definizione, formula, calcolo ed esercizi istantanei della velocità
Il velocità istantanea è definito come il cambiamento istantaneo dello spostamento nel tempo. È un concetto che aggiunge grande precisione allo studio del movimento. Ed è un anticipo rispetto alla velocità media, la cui informazione è molto generale.
Per ottenere la velocità istantanea, diamo un'occhiata al più piccolo intervallo di tempo possibile. Il calcolo differenziale è lo strumento perfetto per esprimere matematicamente questa idea.

Il punto di partenza è la velocità media:

Questo limite è noto come derivato. Nella notazione del calcolo differenziale abbiamo:
))
Ogni volta che il movimento è limitato a una linea retta, si può fare a meno della notazione vettoriale.
Indice articolo
- 1 Calcolo della velocità istantanea: interpretazione geometrica
- 2 Alcuni casi speciali nel calcolo della velocità istantanea
- 3 Risolti esercizi di velocità istantanea
- 3.1 Esercizio 1
- 3.2 Esercizio 2
- 4 Riferimenti
Calcolo della velocità istantanea: interpretazione geometrica
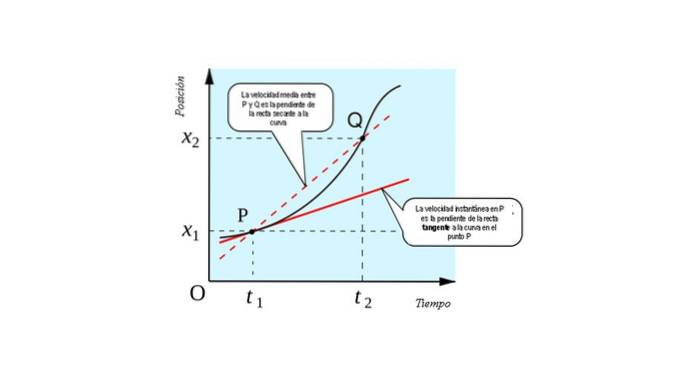
La figura seguente mostra l'interpretazione geometrica del concetto derivativo: è la pendenza della linea tangente alla curva x (t) vs. t in ogni punto.

Potete immaginare come ottenere il limite se il punto Q viene avvicinato a poco a poco al punto P. Verrà un momento in cui entrambi i punti saranno così vicini che non sarete in grado di distinguere l'uno dall'altro..
La linea che li unisce passerà quindi da secante (linea che interseca in due punti) ad essere tangente (linea che tocca la curva in un solo punto). Pertanto, per trovare la velocità istantanea di una particella in movimento dovremmo avere:
- Il grafico della posizione della particella in funzione del tempo. Trovando la pendenza della linea tangente alla curva in ogni istante di tempo, abbiamo la velocità istantanea in ogni punto che occupa la particella.
O bene:
- La funzione di posizione delle particelle x (t), che è derivato per ottenere la funzione di velocità v (t), quindi questa funzione viene valutata in ogni battito t, a comodo. Si presume che la funzione di posizione sia differenziabile.
Alcuni casi speciali nel calcolo della velocità istantanea
-La pendenza della tangente alla curva in P è 0. Una pendenza zero significa che il mobile è fermo e che la sua velocità è ovviamente 0.
-La pendenza della retta tangente alla curva in P è maggiore di 0. La velocità è positiva. Nel grafico sopra significa che il cellulare si sta allontanando da O.
-La pendenza della linea tangente alla curva in P è minore di 0. La velocità sarebbe negativa. Nel grafico sopra non ci sono tali punti, ma in questo caso la particella si avvicinerebbe a O.
-La pendenza della linea tangente alla curva è costante in P e in tutti gli altri punti. In questo caso il grafico è una linea retta e il cellulare ha movimento della linea uniforme MRU (la sua velocità è costante).
In generale, la funzione v (t) è anche una funzione del tempo, che a sua volta può avere una derivata. E se non fosse possibile trovare le derivate delle funzioni x (t) Y v (t)?
In caso di x (t) potrebbe essere che la pendenza - la velocità istantanea - cambi di segno bruscamente. O che sarebbe passato immediatamente da zero a un valore diverso.
In tal caso, il grafico x (t) presenterebbe punti o angoli nei punti di repentini cambiamenti. Molto diverso dal caso rappresentato nell'immagine precedente, in cui la curva x (t) è una curva morbida, senza punti, angoli, discontinuità o cambiamenti improvvisi.
La verità è che per i cellulari reali, le curve morbide sono quelle che meglio rappresentano il comportamento dell'oggetto.
Il movimento in generale è abbastanza complesso. I cellulari possono essere fermati per un po ', accelerare per andare da fermo per avere una velocità e allontanarsi dal punto di partenza, mantenere la velocità per un po', quindi frenare per fermarsi di nuovo e così via..
Di nuovo possono ricominciare e continuare nella stessa direzione. Oppure aziona il contrario e torna indietro. Questo si chiama movimento vario in una dimensione..
Ecco alcuni esempi di calcolo della velocità istantanea che chiariranno l'uso delle definizioni date:
Risolti esercizi di velocità istantanea
Esercizio 1
Una particella si muove lungo una linea retta con la seguente legge di moto:
x (t) = -t3 + 2 tDue + 6 t - 10
Tutte le unità sono nel Sistema Internazionale. Trova:
a) La posizione della particella at = 3 secondi.
b) La velocità media nell'intervallo tra t = 0 se t = 3 s.
c) La velocità media nell'intervallo tra t = 0 se t = 3 s.
d) La velocità istantanea della particella della domanda precedente, at = 1 s.
Risposte
a) Per trovare la posizione della particella, la legge del moto (funzione di posizione) viene valutata at = 3:
x (3) = (-4/3) 33 + 2. 3Due + 6,3 - 10 m = -10 m
Non c'è problema che la posizione sia negativa. Il segno (-) indica che la particella è a sinistra dell'origine O.
b) Nel calcolo della velocità media, la posizione finale e quella iniziale della particella sono richieste nei tempi indicati: x (3) e x (0). La posizione in t = 3 è x (3) ed è nota dal risultato precedente. La posizione at = 0 secondi è x (0) = -10 m.
Poiché la posizione finale è la stessa della posizione iniziale, si conclude immediatamente che la velocità media è 0.
c) La velocità media è il rapporto tra la distanza percorsa e il tempo impiegato. Ora, la distanza è il modulo o l'entità dello spostamento, quindi:
distanza = | x2 - x1 | = | -10 - (-10) | m = 20 m
Notare che la distanza percorsa è sempre positiva.
vm = 20 m / 3 s = 6,7 m / s
d) Qui è necessario trovare la derivata prima della posizione rispetto al tempo. Quindi viene valutato per t = 1 secondo.
x '(t) = -4 tDue + 4 t + 6
x '(1) = -4,1Due + 4,1 + 6 m / s = 6 m / s
Esercizio 2
Di seguito il grafico della posizione di un cellulare in funzione del tempo. Trova la velocità istantanea at = 2 secondi.
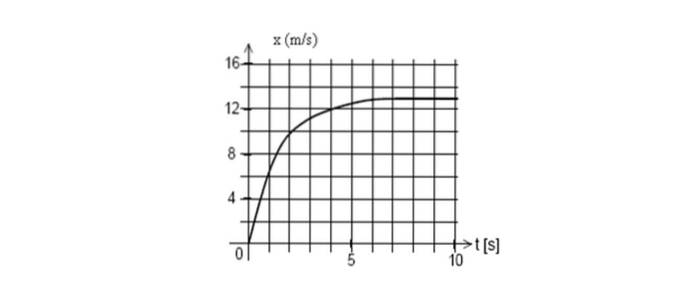
Risposta
Disegna la linea tangente alla curva at = 2 secondi, quindi calcola la sua pendenza, prendendo due punti qualsiasi sulla linea.
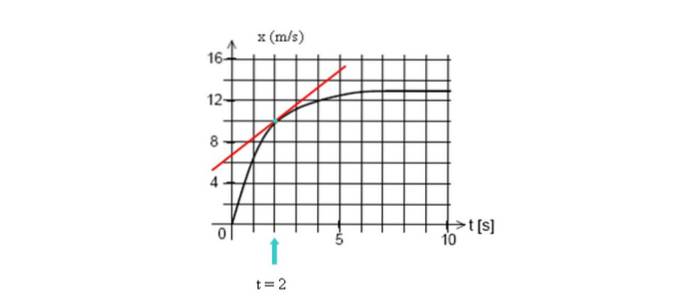
In questo esempio prenderemo due punti facilmente visualizzabili, le cui coordinate sono (2 s, 10 m) e il taglio con l'asse verticale (0 s, 7 m):

Riferimenti
- Giancoli, D. Physics. Principi con applicazioni. 6th Edizione. Prentice Hall. 22-25.
- Resnick, R. (1999). Fisico. Volume 1. Terza edizione in spagnolo. Messico. Azienda editoriale Continental S.A. de C.V. 21-22.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7ma. Edizione. Messico. Cengage Learning Editors. 23-25.



Nessun utente ha ancora commentato questo articolo.