
Vettori nello spazio come rappresentare graficamente, applicazioni, esercizi
UN vettore nello spazio è ognuno rappresentato da un sistema di coordinate dato da X, Y Y z. Quasi sempre l'aereo xy è il piano della superficie orizzontale e l'asse z rappresenta l'altezza (o la profondità).
Gli assi delle coordinate cartesiane mostrati nella figura 1 dividono lo spazio in 8 regioni chiamate ottanti, analogo a come gli assi X - Y dividere l'aereo in 4 quadranti. Avremo quindi il 1 ° ottante, il 2 ° ottante e così via.
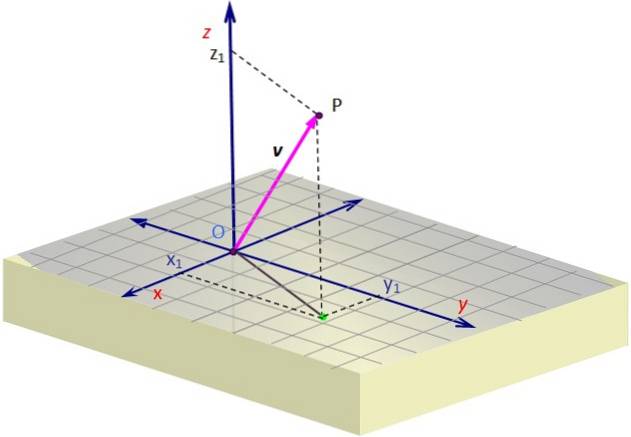
La figura 1 contiene una rappresentazione di un vettore v nello spazio. È necessaria una certa prospettiva per creare l'illusione delle tre dimensioni sul piano dello schermo, che si ottiene disegnando una vista obliqua.
Per rappresentare graficamente un vettore 3D, utilizzare le linee tratteggiate che determinano sulla griglia le coordinate della proiezione o "ombra" di v Sulla superficie x-y. Questa proiezione inizia in O e termina nel punto verde.
Una volta lì, devi continuare lungo la verticale fino all'altezza (o profondità) necessaria in base al valore di z, fino a raggiungere P. Il vettore viene disegnato partendo da O e terminando in P, che nell'esempio è al 1 ° ottante.
Indice articolo
- 1 Applicazioni
- 2 Notazione e rappresentazioni di vettori in 3D
- 2.1 Angoli e coseni direttori di un vettore
- 3 esercizi risolti
- 3.1 -Esercizio 1
- 3.2 -Esercizio 2
- 4 Riferimenti
Applicazioni
I vettori nello spazio sono ampiamente usati nella meccanica e in altri rami della fisica e dell'ingegneria, poiché le strutture che ci circondano richiedono la geometria in tre dimensioni..
I vettori di posizione nello spazio vengono utilizzati per posizionare gli oggetti rispetto a un punto di riferimento chiamato fonte O. Pertanto, sono anche strumenti necessari nella navigazione, ma non solo.
Le forze che agiscono su strutture come bulloni, staffe, cavi, montanti e altro sono di natura vettoriale e orientate nello spazio. Per conoscerne l'effetto è necessario conoscerne l'indirizzo (e anche il suo punto di applicazione).
E spesso la direzione di una forza è conosciuta conoscendo due punti nello spazio che appartengono alla sua linea di azione. In questo modo la forza è:
F = F o
Dove F è l'ampiezza o il modulo della forza e o è il vettore unitario (di modulo 1) diretto lungo la linea di azione di F.
Notazione e rappresentazioni vettoriali 3D
Prima di procedere alla risoluzione di alcuni esempi, esamineremo brevemente la notazione vettoriale 3D.
Nell'esempio in Figura 1, il vettore v, il cui punto di origine coincide con l'origine O e il cui punto finale è il punto P, ha coordinate X Y z positivo, mentre la coordinata Y è negativo. Queste coordinate sono: X1, Y1, z1, che sono precisamente le coordinate di P.
Quindi se abbiamo un vettore legato all'origine, cioè il cui punto di partenza coincide con O, è molto facile indicarne le coordinate, che saranno quelle del punto estremo o P. Per distinguere tra un punto e un vettore, useremo le ultime lettere e parentesi in grassetto, in questo modo:
v = < x1, Y1, z1 >
Mentre il punto P è indicato con parentesi:
P = (x1, Y1, z1)
Un'altra rappresentazione fa uso di vettori unitari io, j Y K che definiscono le tre direzioni dello spazio sugli assi X, Y Y z rispettivamente.
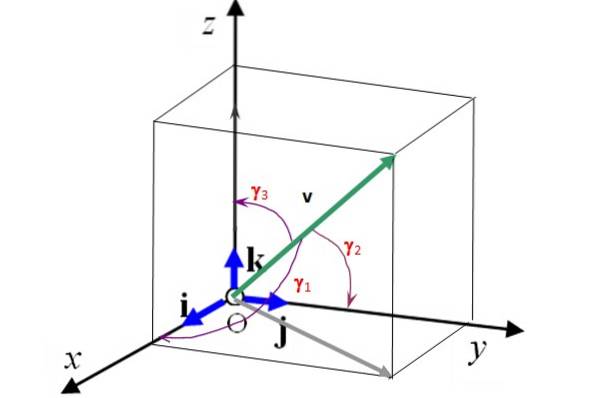
Questi vettori sono perpendicolari tra loro e formano a base ortonormale (vedi figura 2). Ciò significa che un vettore 3D può essere scritto in termini di essi come:
v = vX io + vY j + vz K
Angoli e coseni direzionali di un vettore
La figura 2 mostra anche gli angoli di direttrice γ1, γDue e γ3 rispetto al vettore v fa rispettivamente con gli assi X, Y Y z. Conoscendo questi angoli e la grandezza del vettore, è completamente determinato. Inoltre, i coseni degli angoli del regista soddisfano la seguente relazione:
(cos γ1)Due + (cos γDue)Due + (cos γ3)Due = 1
Esercizi risolti
-Esercizio 1
Nella figura 2 gli angoli γ1, γDue e γ3 rispetto al vettore v di forma del modulo 50 con gli assi coordinati sono rispettivamente: 75,0º, 60,0º e 34,3º. Trova le componenti cartesiane di questo vettore e rappresentalo in termini di vettori unitari io, j Y K.
Soluzione
Proiezione vettoriale v sull'asse X è VX = 50. cos 75º = 12.941. Allo stesso modo, la proiezione di v sull'asse Y è VY = 50 cos 60 º = 25 e infine sull'asse z è Vz = 50. cos 34,3º = 41,3. Adesso v può essere espresso come:
v = 12,9 io + 25.0 j + 41.3 K
-Esercizio 2
Trova le tensioni in ciascuno dei cavi che tengono il secchio nella figura che è in equilibrio, se il suo peso è 30 N.
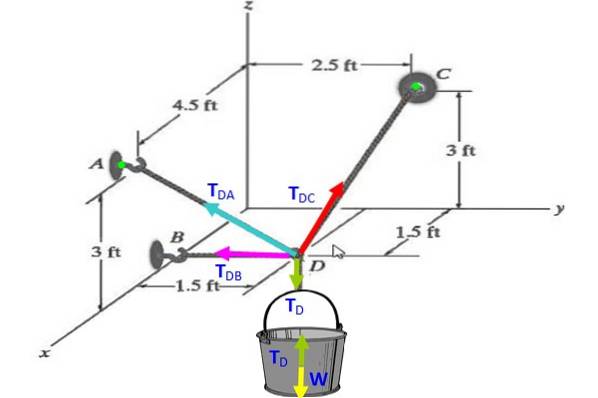
Soluzione
Sul secchio, il diagramma del corpo libero lo indica TD (verde) compensa il peso W (giallo), quindi TD = W = 30 N.
Nel nodo, il vettore TD è diretto verticalmente verso il basso, quindi:
TD = 30 (-K) N.
Per stabilire le tensioni rimanenti, attenersi alla seguente procedura:
Passaggio 1: trova le coordinate di tutti i punti
A = (4.5,0,3) (A è sul piano del muro x-z)
B = (1.5,0,0) (B è sull'asse x)
C = (0, 2.5, 3) (C è sul piano del muro e Z)
D = (1.5, 1.5, 0) (D è sul piano orizzontale x-y)
Passaggio 2: trova i vettori in ciascuna direzione sottraendo le coordinate della fine e dell'inizio
DÀ = <3; -1.5; 3>
DC = <-1.5; 1; 3>
DB = <0; -1.5 ; 0>
Passaggio 3: calcolo di moduli e vettori di unità
Un vettore unitario si ottiene dall'espressione: o = r / r, con r (in grassetto) è il vettore e r (non in grassetto) è il modulo di detto vettore.
DA = (3Due + (-1,5)Due + 3Due)½ = 4,5; DC = ((-1,5) Due + 1Due + 3Due)½ = 3.5
oDÀ = <3; -1.5; 3>4,5 = <0.67 ; -0.33 ; 0.67>
oDC = <-1.5; 1; 3>3,5 = <-0.43; 0.29; 0.86>
oDB = <0; -1; 0>
oD = <0; 0; -1>
Passaggio 4: esprimere tutte le sollecitazioni come vettori
TDÀ = TDÀ oDÀ = TDÀ<0.67 ; -0.33 ; 0.67>
TDC = TDC oDC = TDC <-0.43; 0.29; 0.86>
TDB = TDB oDB = TDB <0; -1; 0>
TD = 30 <0; 0; -1>
Passaggio 5: applicare la condizione di equilibrio statico e risolvere il sistema di equazioni
Infine, al bucket viene applicata la condizione di equilibrio statico, in modo che la somma vettoriale di tutte le forze sul nodo sia zero:
TDÀ + TDC + TDB + TD = 0
Poiché le sollecitazioni sono nello spazio, risulterà in un sistema di tre equazioni per ogni componente (X, e e z) delle tensioni.
0.67 TDÀ -0.43 TDC + 0 TDB = 0
-0,33 TDÀ + 0,29 TDC - TDB = 0
0.67 TDÀ + 0,86 TDC +0 TDB - 30 = 0
La soluzione è: TDÀ = 14,9 N; TDÀ = 23,3 N; TDB = 1,82 N
Riferimenti
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Volume 1. Cinematica. 31-68.
- Fisico. Modulo 8: vettori. Estratto da: frtl.utn.edu.ar
- Hibbeler, R. 2006. Meccanica per ingegneri. Statico. 6a edizione. Continental Publishing Company. 15-53.
- Calcolatrice di addizione vettoriale. Estratto da: 1728.org



Nessun utente ha ancora commentato questo articolo.