
Equazione di direzione vettoriale della linea, esercizi risolti
È compreso da direttore vettoriale uno che definisce la direzione di una linea, nel piano o nello spazio. Pertanto, un vettore parallelo alla linea può essere considerato come un vettore direttivo della stessa.
Ciò è possibile grazie a un assioma della geometria euclidea che dice che due punti definiscono una linea. Quindi il segmento orientato formato da questi due punti definisce anche un vettore direttore di detta linea.
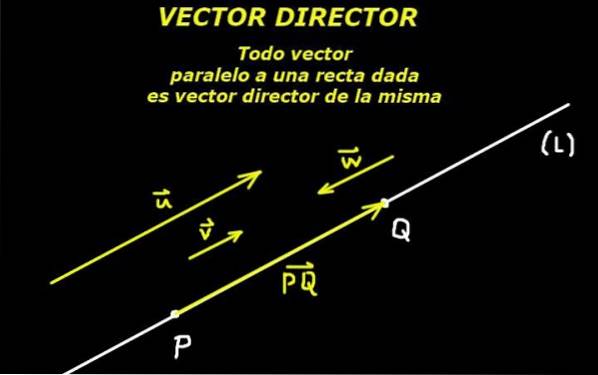
Dato un punto P appartenente alla linea (L) e dato un vettore regista o di quella linea, la linea è completamente determinata.
Indice articolo
- 1 Equazione della retta e vettore direttore
- 1.1 Equazione parametrica della retta
- 2 La linea in forma vettoriale
- 2.1 Esempio 2
- 2.2 Forma continua della linea e del vettore direttore
- 3 Forma generale dell'equazione della retta
- 3.1 Esempio 3
- 4 Forma standard dell'equazione della retta
- 4.1 Esempio 4
- 5 Esercizi risolti
- 5.1 -Esercizio 1
- 5.2 -Esercizio 2
- 6 Riferimenti
Equazione della retta e vettore direttore
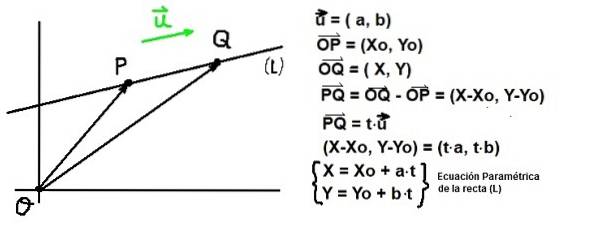
Dato un punto P di coordinate D: (Xo, I) e un vettore o regista di una scala (L), tutto punto Q di coordinate Q: (X, Y) deve soddisfare che il vettore PQ essere parallelo a u. Quest'ultima condizione è garantita se PQ è proporzionale a o:
PQ = t⋅o
nell'espressione precedente t è un parametro che appartiene ai numeri reali.
Se le componenti cartesiane di PQ e di o L'equazione di cui sopra è scritta come segue:
(X-Xo, Y-Yo) = t⋅ (a, b)
Se le componenti dell'uguaglianza vettoriale sono equalizzate, abbiamo la seguente coppia di equazioni:
X - Xo = a⋅t Y Y - I = b⋅t
Equazione parametrica della retta
Le coordinate X e Y di un punto sulla linea (L) passando per un punto di coordinate (Xo, io) ed è parallelo a direttore vettoriale o= (a, b) sono determinati assegnando valori reali al parametro variabile t:
X = Xo + a⋅t; Y = I + b⋅t
Esempio 1
Per illustrare il significato dell'equazione parametrica della retta, prendiamo come vettore di direzione
o = (a, b) = (2, -1)
e come punto noto della linea il punto
P = (Xo, I) = (1, 5).
L'equazione parametrica della retta è:
X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞
Per illustrare il significato di questa equazione, viene mostrata la figura 3, dove il parametro t cambia valore e punto Q di coordinate (X, Y) prendere diverse posizioni sul rettilineo.
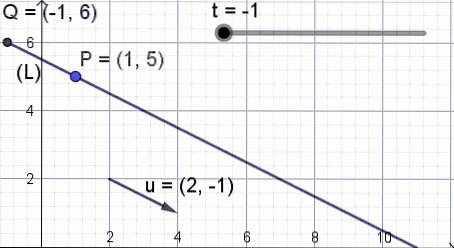
La linea in forma vettoriale
Dato un punto P sulla retta e il suo vettore direttrice u, l'equazione della retta può essere scritta in forma vettoriale:
OQ = OPERAZIONE + λ⋅o
Nell'equazione precedente Q è un punto qualsiasi ma appartiene alla linea e λ un numero reale.
L'equazione vettoriale della linea è applicabile a qualsiasi numero di dimensioni, anche una iperline può essere definita.
Nel caso tridimensionale per un regista vettoriale o= (a, b, c) e un punto P = (Xo, Yo, Zo), le coordinate di un punto generico Q = (X, Y, Z) appartenente alla linea è:
(X E Z) = (Xo, Yo, Zo) + λ⋅ (a, b, c)
Esempio 2
Considera ancora la linea che ha come vettore direzionale
o = (a, b) = (2, -1)
e come punto noto della linea il punto
P = (Xo, I) = (1, 5).
L'equazione vettoriale di questa linea è:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Forma continua della linea e del vettore regista
Partendo dalla forma parametrica, azzerando ed equiparando il parametro λ, abbiamo:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
Questa è la forma simmetrica dell'equazione della retta. Sento che per, b Y c sono i componenti del vettore director.
Esempio 3
Considera la linea che ha come vettore direzionale
o = (a, b) = (2, -1)
e come punto noto della linea il punto
P = (Xo, I) = (1, 5). Trova la sua forma simmetrica.
La forma simmetrica o continua della linea è:
(X - 1) / 2 = (Y - 5) / (- 1)
Forma generale dell'equazione della retta
L'equazione che ha la seguente struttura è nota come forma generale della linea nel piano XY:
A⋅X + B⋅Y = C
L'espressione per la forma simmetrica può essere riscritta per avere la forma generale:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
rispetto alla forma generale della linea è:
A = b, B = -a e C = b⋅Xo - a⋅Yo
Esempio 3
Trova la forma generale della retta il cui vettore direttrice è u = (2, -1)
e che passa per il punto P = (1, 5).
Per trovare la forma generale possiamo utilizzare le formule fornite, tuttavia verrà scelto un percorso alternativo.
Iniziamo trovando il vettore duale w del vettore direttore u, definito come il vettore ottenuto scambiando le componenti di u e moltiplicando il secondo per -1:
w= (-1, -2)
il doppio vettore w corrisponde ad una rotazione in senso orario di 90 ° del vettore regista v.
Ci moltiplichiamo scalare w con (X, Y) e con (Xo, io) e abbiniamo:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2⋅5 = -11
rimanendo infine:
X + 2Y = 11
Forma standard dell'equazione della retta
È conosciuta come la forma standard della linea nel piano XY, quella che ha la seguente struttura:
Y = m⋅X + d
dove m rappresenta la pendenza ed l'intercetta con l'asse Y..
Dato il vettore di direzione u = (a, b), la pendenza m è b / a.
Y d si ottiene sostituendo X e Y al punto noto Xo, I:
I = (b / a) Xo + d.
In breve, m = b / a ed = I - (b / a) Xo
Notare che la pendenza m è il quoziente tra i componenti Y del vettore regista e del componente X dello stesso.
Esempio 4
Trova la forma standard della retta il cui vettore direttrice è u = (2, -1)
e che passa per il punto P = (1, 5).
m = -½ ed = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Esercizi risolti
-Esercizio 1
Trova un vettore direttrice della retta (L) che è l'intersezione del piano (Π): X - Y + Z = 3 e il piano (Ω): 2X + Y = 1.
Quindi scrivi la forma continua dell'equazione della retta (L).
Soluzione
Dall'equazione del gioco Y del piano (Ω): Y = 1 -2X
Quindi sostituiamo nell'equazione del piano (Π):
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Quindi parametrizziamo X, scegliamo la parametrizzazione X = λ
Ciò significa che la linea ha un'equazione vettoriale data da:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
che può essere riscritto come:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
con cui è chiaro che il vettore o = (1, -2, -3) è un vettore di direzione della linea (L).
La forma continua della linea (L) è:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Esercizio 2
Dato l'aereo 5X + per Y + 4Z = 5
e la retta la cui equazione è X / 1 = (Y-2) / 3 = (Z -2) / (- 2)
Determina il valore di per in modo che il piano e la linea siano paralleli.
Soluzione 2
Il vettore n = (5, a, 4) è un vettore normale al piano.
Il vettore o = (1, 3, -2) è un vettore direttore della linea.
Se la linea è parallela all'aereo, allora n • v = 0.
(5, per, 4)•(1, 3, -2) = 5 +3per -8 = 0 ⇒ per= 1.
Riferimenti
- Fleming, W. e Varberg, D. E. (1989). Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. (2006). Algebra lineare. Pearson Education.
- Leal, J. M. e Viloria, N. G. (2005). Geometria analitica piana. Mérida - Venezuela: Editoriale Venezolana C. A.
- Navarro, Rocio. Vettori. Estratto da: books.google.co.ve.
- Pérez, C. D. (2006). Precalculation. Pearson Education.
- Prenowitz, W. 2012. Concetti di base della geometria. Rowman e Littlefield.
- Sullivan, M. (1997). Precalculation. Pearson Education.



Nessun utente ha ancora commentato questo articolo.