
Concetto di variazione lineare, esempi, esercizio risolto

Il variazione lineare si verifica tra due grandezze fisiche quando il grafico che le rappresenta è una linea retta. È equivalente ad affermare che le variabili sono in dipendenza lineare, in modo tale che se chiamiamo una di esse "y" e l'altra "x", saranno messe in relazione tramite l'espressione matematica:
y = mx + b
In questa formula, m e b sono numeri reali. Il valore di m rappresenta la pendenza o inclinazione della linea -che è sempre costante- eb è il taglio della linea con l'asse verticale.

Ogni fenomeno che risponde a una variazione lineare ha nomi diversi per le variabili, come vedremo negli esempi seguenti. Tuttavia, la forma matematica dell'equazione è la stessa.
Sperimentalmente si può stabilire se esiste una relazione lineare tra due quantità, misurando le coppie di valori (x, y).
I punti così ottenuti vengono tracciati su carta millimetrata e si osserva se hanno un andamento lineare, cioè se esiste una linea che si adatta adeguatamente ai dati sperimentali.
In primo luogo, questa linea può essere tracciata visivamente, ma per mezzo di un file regressione lineare si possono trovare analiticamente i valori di meb della retta che meglio si adattano ai punti sperimentali.
Indice articolo
- 1 Esempi di variazione lineare
- 1.1 Velocità nel moto rettilineo variata in modo uniforme
- 1.2 Dilatazione termica
- 1.3 Posizione di un mobile a velocità costante
- 1.4 Altezza di una persona
- 1.5 Scale di temperatura
- 1.6 Pressione e profondità
- 2 Esercizio risolto
- 2.1 Costo della guida
- 3 Riferimenti
Esempi di variazione lineare
Numerosi sono i fenomeni naturali, così come le relazioni stabilite tra gli standard di misura, che sono dovuti alla variazione lineare, ad esempio:
Velocità nel moto rettilineo variata in modo uniforme
La velocità in funzione del tempo v (t) di un mobile che si muove lungo una linea con accelerazione costante ae velocità iniziale vo diverso da 0. Questo movimento è noto come moto rettilineo uniformemente variato e l'equazione per la velocità è:
v (t) = vo + a
Dilatazione termica
Un altro fenomeno naturale la cui variazione è lineare è l'aumento della lunghezza che una verga o un filo subisce quando viene riscaldata..
Infatti, quando la temperatura di un oggetto aumenta, aumentano anche le sue dimensioni, e questo aumento dipende dalla variazione della temperatura ΔT e da una quantità chiamata coefficiente di espansione lineare indicato dalla lettera greca α:
L = Lo + α ΔT
In questa espressione L è la lunghezza finale dell'oggetto e Lo è la sua lunghezza iniziale.
Posizione di un mobile a velocità costante
Un cellulare con velocità costante si muove sempre in linea retta. Se la linea retta è l'asse x orizzontale, la posizione x (t) in qualsiasi istante è data da:
x (t) = xo + vt
Dove xo è la posizione iniziale, v è la velocità et è il tempo. In questo modo si dice che la posizione x varia linearmente con il tempo t.
Altezza di una persona
Medici e antropologi possono stimare l'altezza di una persona misurando la lunghezza del femore..
Più una persona è alta, più lunghe sono le gambe, quindi esistono modelli lineari per prevedere l'altezza di un adulto H (in pollici) se la lunghezza L (anche in pollici) del suo femore è nota, secondo l'equazione:
H = 1,880⋅L + 32,010
Scale di temperatura
Le scale Celsius e Fahrenheit vengono utilizzate quotidianamente per misurare le temperature. Quest'ultima scala è comunemente usata nei paesi di lingua inglese. C'è un'equivalenza per passare dall'uno all'altro:
F = (9/5) C + 32
Dove F è la temperatura in gradi Fahrenheit e C è la temperatura in gradi Celsius.
Pressione e profondità
La pressione assoluta P in un fluido incomprimibile come l'acqua, la cui densità costante è ρ, varia in funzione della profondità h come:
P = Po + ρgh
Dove Po è la pressione sulla superficie libera del liquido. Se il liquido è in un contenitore aperto all'atmosfera, questa pressione è semplicemente la pressione atmosferica PATM, poter scrivere quindi:
P = PATM + ρgh
La pressione atmosferica a livello del mare è di circa 101 kPa. Questa relazione tra P e h significa che la pressione aumenta linearmente con la profondità..

Esercizio risolto
Costo di guida
Il costo mensile C di guida di un'auto include un costo mensile fisso Co più il costo del chilometraggio o del chilometraggio percorso ogni mese. Un guidatore osserva che in un dato mese il costo della guida era di $ 380 per 480 miglia e il mese successivo era di $ 460 per 800 miglia.
Sia d il numero di miglia percorse al mese dal conducente, con i dati forniti, trova:
a) La variazione lineare tra C e d.
b) Quanto costerebbe al mese per guidare l'auto in un viaggio di 1.500 miglia?
c) Il grafico di C contro d.
Soluzione a
Supponiamo che le variabili abbiano una relazione data da:
C = Co + Anno Domini
Dove A e Co sono costanti da determinare. A è la pendenza della linea che rappresenta graficamente la relazione tra C e d. Co è il taglio con l'asse verticale, il costo mensile fisso che l'autista deve pagare per il solo fatto di avere l'auto a disposizione. Ciò potrebbe includere costi di manutenzione e tasse, ad esempio.
Per determinare inequivocabilmente una linea, è necessario conoscerne la pendenza. Per questo abbiamo i punti:
P1: 480 miglia, $ 380
PDue: 800 miglia, $ 460
Questi punti, di coordinate (d, C) o (distanza, costo) sono analoghi ai punti di coordinate (x, y) del piano cartesiano, ciò che cambia sono i nomi. La pendenza A della linea è quindi data da:
A = (CDue - C1) / (dDue - d1)
A = [(460 - 380) $ / (800 - 480) miglia] = (1/4) $ / miglio
La pendenza della linea rappresenta il costo per miglio, in questo modo:
C = Co + A.d = Co + (1/4) .d
Per determinare il costo della base Co Si prende questa equazione e si sostituisce uno dei punti che sappiamo appartenerle, ad esempio P1:
380 $ = Co + [(1/4) $ / miglio]. 480 miglia → 380 $ = C.o + $ 120
Co = $ 260
Ora possiamo formulare il modello di variazione lineare come:
C = 260 + (1/4) d
Soluzione b
Il costo mensile per viaggiare 1500 miglia è:
C = 260 + (1/4) x $ 1500 = $ 635
Soluzione c
Il grafico di C contro d è:
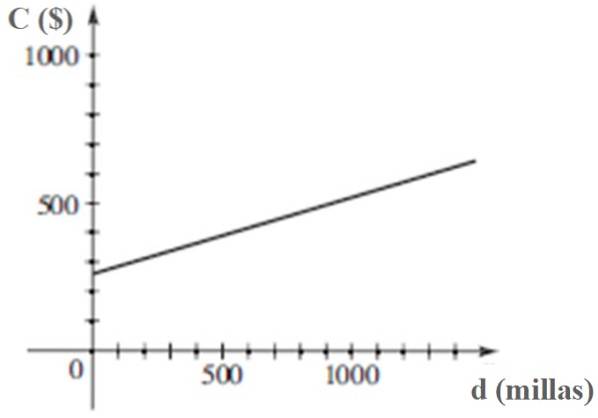
Riferimenti
- Baldor. 1977. Algebra elementare. Edizioni culturali venezuelane.
- Hoekenga, C. equazioni lineari nella scienza. Estratto da: visionlearning.com.
- Hoffman, J. Selezione di argomenti di matematica. Volume 2.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5 °. Edizione. Cengage Learning.
- Zill, D. 1984. Algebra e trigonometria. Mcgraw hill.



Nessun utente ha ancora commentato questo articolo.