
Lavoro meccanico cos'è, condizioni, esempi, esercizi
Il lavoro meccanico È definito come il cambiamento dello stato energetico di un sistema, causato dall'azione di forze esterne come la gravità o l'attrito. Le unità di lavoro meccanico nel Sistema Internazionale (SI) sono newton x metro o joule, abbreviato con J.
Matematicamente è definito come il prodotto scalare del vettore forza e del vettore spostamento. sì F è la forza costante e l è lo spostamento, entrambi i vettori, il lavoro W è espresso come: W = F ● l

Quando la forza non è costante, allora dobbiamo analizzare il lavoro svolto quando gli spostamenti sono molto piccoli o differenziali. In questo caso, se si considera il punto A come punto di partenza e B come punto di arrivo, il lavoro totale si ottiene sommando ad esso tutti i contributi. Ciò equivale al calcolo del seguente integrale:
Variazione di energia del sistema = Lavoro svolto da forze esterne
ΔE = Wext
Quando l'energia viene aggiunta al sistema, W> 0 e quando l'energia viene sottratta W<0. Ahora bien, si ΔE = 0, puede significar que:
-Il sistema è isolato e non ci sono forze esterne che agiscono su di esso.
-Ci sono forze esterne, ma non stanno lavorando sul sistema.
Poiché la variazione di energia è uguale al lavoro svolto dalle forze esterne, l'unità SI di energia è anche il joule. Questo include qualsiasi tipo di energia: cinetica, potenziale, termica, chimica e altro ancora..
Indice articolo
- 1 Condizioni per l'esistenza del lavoro meccanico
- 1.1 Segni di lavoro
- 2 Esempi di lavori meccanici
- 3 Il teorema dell'energia cinetica di lavoro
- 3.1 Lavoro svolto per allungare una molla
- 4 esercizi
- 4.1 Esercizio 1
- 4.2 Esercizio 2
- 5 Riferimenti
Condizioni per l'esecuzione di lavori meccanici
Abbiamo già visto che il lavoro è definito come un prodotto puntuale. Prendiamo la definizione di lavoro svolto da una forza costante e applichiamo il concetto di prodotto scalare tra due vettori:
W = F ● l = F.l.cos θ
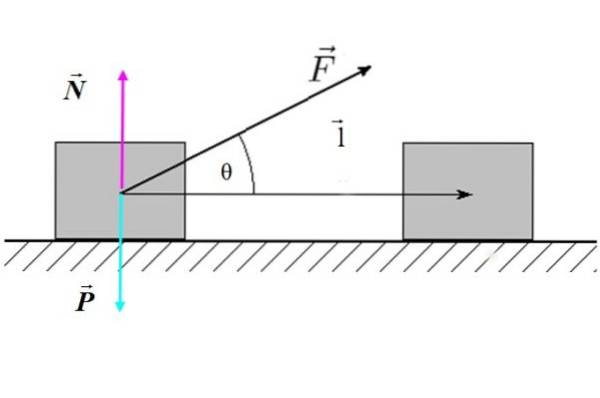
Dove F è l'entità della forza, l è l'entità dello spostamento e θ è l'angolo tra la forza e lo spostamento. Nella figura 2 è riportato un esempio di una forza esterna inclinata che agisce su un blocco (il sistema), che produce uno spostamento orizzontale.

Riscrivere il lavoro come segue:
W = (F. cos θ). l
Possiamo affermare che solo la componente della forza parallela allo spostamento: F. cos θ eè in grado di lavorare. Se θ = 90º allora cos θ = 0 e il lavoro sarebbe zero.
Pertanto si conclude che le forze perpendicolari allo spostamento non svolgono un lavoro meccanico.
Nel caso della figura 2, né la forza normale N né il peso P funzionano, poiché entrambi sono perpendicolari allo spostamento l.
I segni del lavoro
Come spiegato sopra, W Può essere positivo o negativo. Quando cos θ> 0, il lavoro svolto dalla forza è positivo, poiché ha la stessa direzione di movimento.
sì cos θ = 1, forza e spostamento sono paralleli e il lavoro è massimo.
Nel caso in cui cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
quando cos θ = -1, la forza è completamente opposta allo spostamento, come l'attrito cinetico, il cui effetto è di rallentare l'oggetto su cui agisce. Quindi il lavoro è minimo.
Ciò concorda con quanto detto all'inizio: se il lavoro è positivo, si aggiunge energia al sistema, se è negativa si sottrae.
Rete Wnetto È definito come la somma del lavoro svolto da tutte le forze agenti sul sistema:
Wnetto = ∑Wio
Possiamo quindi concludere che per garantire l'esistenza del lavoro meccanico netto è necessario che:
-Le forze esterne agiscono sull'oggetto.
-Queste forze non sono tutte perpendicolari allo spostamento (cos θ ≠ 0).
-I lavori svolti da ciascuna forza non si annullano a vicenda.
-C'è uno spostamento.
Esempi di lavorazioni meccaniche
-Ogni volta che è necessario mettere in movimento un oggetto da fermo, è necessario eseguire lavori meccanici. Ad esempio spingendo un frigorifero o un baule pesante su una superficie orizzontale.
-Un altro esempio di una situazione in cui è necessario eseguire un lavoro meccanico è cambiare la velocità di una palla in movimento..
-Il lavoro è necessario per sollevare un oggetto a una certa altezza dal pavimento.
Ora, ci sono situazioni altrettanto comuni in cui non il lavoro viene fatto, anche se le apparenze indicano il contrario. Abbiamo detto che per sollevare un oggetto a una certa altezza bisogna lavorare, quindi portiamo l'oggetto, lo solleviamo sopra la nostra testa e lo teniamo lì. Stiamo lavorando?
Apparentemente sì, perché se l'oggetto è pesante le braccia si stancheranno in breve tempo, tuttavia non importa quanto sia difficile, dal punto di vista della Fisica non si fa nessun lavoro. Perchè no? Bene, perché l'oggetto non si muove.
Un altro caso in cui, pur avendo una forza esterna, non svolge un lavoro meccanico è quando la particella ha un moto circolare uniforme.
Ad esempio, un bambino che gira una pietra legata a una corda. La tensione delle corde è la forza centripeta che permette alla pietra di ruotare. Ma in ogni momento questa forza è perpendicolare allo spostamento. Quindi non esegue lavori meccanici, sebbene favorisca il movimento.
Il teorema dell'energia cinetica del lavoro
L'energia cinetica del sistema è quella che possiede in virtù del suo movimento. sì m è la massa e v è la velocità del movimento, l'energia cinetica è indicata con K ed è data da:
K = ½ mvDue
Per definizione, l'energia cinetica di un oggetto non può essere negativa, poiché sia la massa che il quadrato della velocità sono sempre quantità positive. L'energia cinetica può essere 0, quando l'oggetto è a riposo.
Per modificare l'energia cinetica di un sistema, è necessario variare la sua velocità - considereremo che la massa rimane costante, anche se non è sempre così. Ciò richiede di fare un lavoro di rete sul sistema, quindi:
Wnetto = ΔK
Questo è il teorema dell'energia cinetica. Si afferma che:
Il lavoro netto è uguale alla variazione dell'energia cinetica del sistema
Nota che sebbene K sia sempre positivo, ΔK può essere positivo o negativo, poiché:
ΔK = Kfinale - K iniziale
sì Kfinale >K iniziale il sistema ha guadagnato energia e ΔK> 0. Al contrario, se Kfinale < K iniziale, il sistema ha smesso di funzionare.
Lavoro svolto per allungare una molla
Quando una molla è tesa (o compressa), è necessario lavorare. Questo lavoro viene immagazzinato in primavera, consentendo a questo a sua volta di lavorare, diciamo, su un blocco che è attaccato a una delle sue estremità..
La legge di Hooke afferma che la forza esercitata da una molla è una forza di ripristino - è contraria allo spostamento - e anche proporzionale a detto spostamento. La costante di proporzionalità dipende da come è la molla: morbida e facilmente deformabile o rigida.
Questa forza è data da:
Fr = -kx
Nell'espressione, Fr è la forza, K è la costante primaverile e X è lo spostamento. Il segno negativo indica che la forza esercitata dalla molla si oppone allo spostamento.
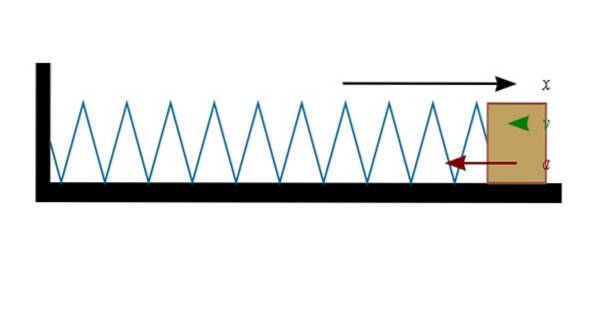
Se la molla è compressa (a sinistra nella figura), il blocco alla sua estremità si sposterà a destra. E quando la molla è allungata (a destra) il blocco vorrà spostarsi a sinistra.
Per comprimere o allungare la molla, deve fare il lavoro qualche agente esterno, e poiché si tratta di una forza variabile, per calcolare tale lavoro, dobbiamo usare la definizione data all'inizio:
È molto importante notare che questo è il lavoro svolto dall'agente esterno (la mano di una persona, ad esempio) per comprimere o allungare la molla. Ecco perché il segno negativo non appare. E poiché le posizioni sono quadrate, non importa se si tratta di compressioni o allungamenti..
Il lavoro che la molla a sua volta farà sul blocco è:
Wprimavera = -Wext
Formazione
Esercizio 1
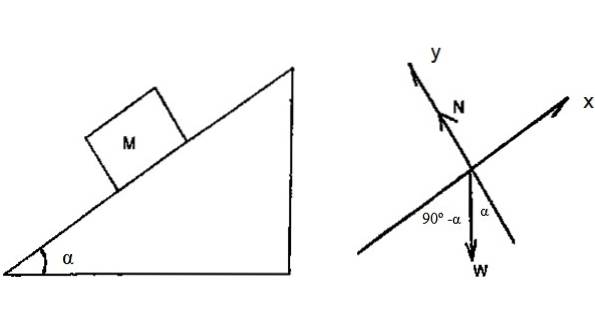
Il blocco di figura 4 ha massa M = 2 kg e scorre lungo il piano inclinato senza attriti, con α = 36,9º. Supponendo che sia consentito lo scorrimento da fermo dalla sommità del piano, la cui altezza è h = 3 m, trova la velocità con cui il blocco raggiunge la base del piano, utilizzando il teorema dell'energia cinetica di lavoro.

Soluzione
Il diagramma a corpo libero mostra che l'unica forza in grado di lavorare sul blocco è il peso. Più preciso: la componente del peso lungo l'asse x.
La distanza percorsa dal blocco sull'aereo viene calcolata utilizzando la trigonometria:
d = 3 / (cos 36,9º) m = 3,75 m
Wpeso = (Mg). d. cos (90-α) = 2 x 9,8 x 3,75 x cos 53,1 º J = 44,1 J
Per teorema dell'energia cinetica di lavoro:
Wnetto = ΔK
Wnetto = Wpeso
ΔK = ½ MvFDue- ½ MvoDue
Dal momento che viene rilasciato dal riposo, vo = 0, Quindi:
Wnetto = ½ MvFDue

Esercizio 2
Una molla orizzontale, la cui costante è k = 750 N / m, è fissata a un'estremità a un muro. Una persona comprime l'altra estremità per una distanza di 5 cm. Calcola: a) La forza esercitata dalla persona, b) Il lavoro che ha fatto per comprimere la molla.
Soluzione
a) L'entità della forza applicata dalla persona è:
F = kx = 750 N / m. 5x10 -Due m = 37,5 N.
b) Se la fine della molla è originariamente in x1 = 0, per portarlo da lì alla posizione finale xDue = 5 cm, è necessario eseguire il seguente lavoro, in base al risultato ottenuto nella sezione precedente:
Wext = ½ k (xDueDue - X1Due) = 0,5 x 750 x (0,05Due -0Due) J = 0,9375 J.
Riferimenti
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 2. Dinamica. A cura di Douglas Figueroa (USB).
- Iparraguirre, L. 2009. Meccanica di base. Collezione di scienze naturali e matematica. Distribuzione online gratuita.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Fisica Libretexts. Teorema dell'energia del lavoro. Recupero da: phys.libretexts.org
- Lavoro ed energia. Recupero da: physics.bu.edu
- Lavoro, energia e potere. Estratto da: ncert.nic.in


Nessun utente ha ancora commentato questo articolo.