
Caratteristiche del colpo parabolico obliquo, formule, equazioni, esempi
Il tiro parabolico obliquo è un caso particolare di moto in caduta libera in cui la velocità iniziale del proiettile forma un certo angolo con l'orizzontale, risultando in una traiettoria parabolica.
La caduta libera è un caso di moto con accelerazione costante, in cui l'accelerazione è quella di gravità, che punta sempre verticalmente verso il basso e ha una magnitudine di 9,8 m / s ^ 2. Non dipende dalla massa del proiettile, come dimostrò Galileo Galilei nel 1604.
Se la velocità iniziale del proiettile è verticale, la caduta libera ha traiettoria diritta e verticale, ma se la velocità iniziale è obliqua allora la traiettoria di caduta libera è una curva parabolica, fatto dimostrato anche da Galileo.
Esempi di movimento parabolico sono la traiettoria di una palla da baseball, il proiettile sparato da un cannone e il getto d'acqua che esce da un tubo..
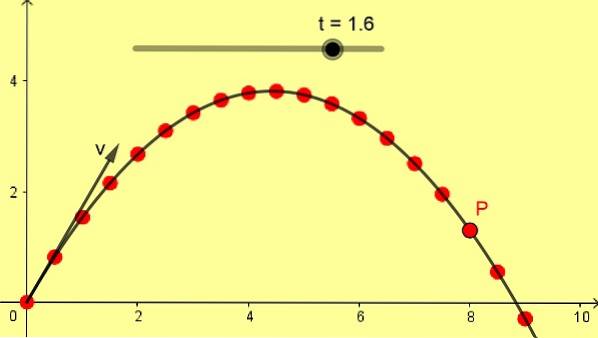
La figura 1 mostra un pescaggio parabolico obliquo di 10 m / s con un angolo di 60º. La scala è in metri e le posizioni successive di P sono prese con una differenza di 0,1 s a partire dall'istante iniziale di 0 secondi.
Indice articolo
- 1 Formule
- 1.1 Posizione e velocità
- 2 Equazioni
- 2.1 Equazioni parametriche
- 2.2 Equazione della traiettoria
- 3 esempi
- 3.1 Esempio 1
- 3.2 Esempio 2
- 3.3 Esempio 3
- 4 Riferimenti
Formule
Il moto di una particella è completamente descritto se la sua posizione, la sua velocità e la sua accelerazione sono note in funzione del tempo..
Il movimento parabolico risultante da un colpo obliquo è la sovrapposizione di un movimento orizzontale a velocità costante, più un movimento verticale con accelerazione costante pari all'accelerazione di gravità..
Le formule che si applicano al tiraggio parabolico obliquo sono quelle che corrispondono ad un moto con accelerazione costante a = g, si noti che il grassetto è stato utilizzato per indicare che l'accelerazione è una quantità vettoriale.
Posizione e velocità
In un movimento con accelerazione costante la posizione dipende matematicamente dal tempo in forma quadratica.
Se denotiamo r(t) posizione alla volta t, ro la posizione nell'istante iniziale, vo velocità iniziale, g accelerazione e t = 0 come istante iniziale la formula che fornisce la posizione per ogni istante di tempo t è:
r(t) = ro + vo t + ½ g tDue
Il grassetto nell'espressione sopra indica che si tratta di un'equazione vettoriale.
La velocità in funzione del tempo si ottiene prendendo la derivata rispetto at della posizione e il risultato è:
v(t) = vo + g t
E per ottenere l'accelerazione in funzione del tempo, la derivata della velocità rispetto a t risultante:
per(t) = g
Quando il tempo non è disponibile, c'è una relazione tra velocità e posizione, che è data da:
vDue = voDue - 2 g (e - io)
Equazioni
Successivamente troveremo le equazioni che si applicano a un colpo parabolico obliquo in forma cartesiana.
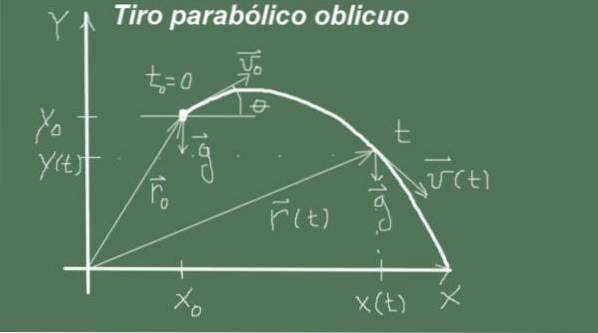
Il movimento inizia nell'istante t = 0 con posizione di partenza (xo, io) e velocità di grandezza vo e l'angolo θ, cioè, il vettore di velocità iniziale è (vo cosθ, vo senθ). Il movimento procede con accelerazione
g = (0, -g).
Equazioni parametriche
Se si applica la formula vettoriale che dà la posizione in funzione del tempo e le componenti sono raggruppate ed equalizzate, si otterranno le equazioni che danno le coordinate della posizione in qualsiasi istante di tempo t.
x (t) = xo + vbue t
y (t) = yo + vHey t -½ g tDue
Allo stesso modo, abbiamo le equazioni per le componenti della velocità in funzione del tempo.
vX(t) = vbue
vY(t) = vHey - g t
Dove: vbue = vo cosθ; vHey = vo senθ
Equazione della traiettoria
y = A x ^ 2 + B x + C
A = -g / (2 vbue^ 2)
B = (vHey/ vbue + g xo/ vbue^ 2)
C = (eo - vHey Xo / vbue)
Esempi
Esempio 1
Rispondi alle seguenti domande:
a) Perché nei problemi di tiraggio parabolico l'effetto dell'attrito con l'aria viene solitamente trascurato??
b) La forma dell'oggetto ha qualche importanza nel tiro parabolico?
Risposte
a) Affinché il movimento di un proiettile sia parabolico, è importante che la forza di attrito dell'aria sia molto inferiore al peso dell'oggetto che viene lanciato.
Se viene lanciata una palla di sughero o un materiale leggero, la forza di attrito è paragonabile al peso e la sua traiettoria non può avvicinarsi a una parabola.
Se invece si tratta di un oggetto pesante come una pietra, la forza di attrito è trascurabile rispetto al peso della pietra e la sua traiettoria si avvicina a una parabola.
b) Anche la forma dell'oggetto lanciato è rilevante. Se un foglio di carta viene lanciato a forma di aeroplano, il suo movimento non sarà in caduta libera o parabolico, poiché la forma favorisce la resistenza dell'aria.
Se invece lo stesso foglio di carta viene compattato in una palla, il movimento risultante è molto simile a una parabola.
Esempio 2
Un proiettile viene lanciato dal suolo orizzontale con una velocità di 10 m / se un angolo di 60º. Questi sono gli stessi dati con cui è stata elaborata la figura 1. Con questi dati, trovare:
a) Momento in cui raggiunge l'altezza massima.
b) L'altezza massima.
c) Velocità alla massima altezza.
d) Posizione e velocità a 1,6 s.
e) Nel momento in cui colpisce di nuovo il suolo.
f) La portata orizzontale.
Soluzione a)
La velocità verticale in funzione del tempo è
vY(t) = vHey - g t = vo sinθ - g t = 10 sin60º - 9,8 t = 8,66 - 9,8 t
Nel momento in cui viene raggiunta l'altezza massima, la velocità verticale è nulla per un istante.
8,66 - 9,8 t = 0 ⇒ t = 0,88 s.
Soluzione b)
L'altezza massima è data dalla coordinata Y per l'istante in cui si raggiunge tale altezza:
e (0,88 s) = Io + vado t -½ g t ^Due = 0 + 8,66 * 0,88-½ 9,8 0,88 ^Due =
3,83 m
L'altezza massima è quindi 3,83 m.
Soluzione c)
La velocità alla massima altezza è orizzontale:
vX(t) = vbue = vo cosθ = 10 cos60º = 5 m / s
Soluzione d)
La posizione a 1,6 s è:
x (1,6) = 5 * 1,6 = 8,0 m
e (1.6) = 8,66 * 1,6-½ 9,8 1,6Due = 1,31 m
Soluzione e)
Quando la coordinata y tocca il suolo, allora:
y (t) = 8,66 * t-½ 9,8 tDue = 0 ⇒ t = 1,77 s
Soluzione f)
La portata orizzontale è la coordinata x proprio nell'istante in cui tocca il suolo:
x (1,77) = 5 * 1,77 = 8,85 m
Esempio 3
Trova l'equazione della traiettoria con i dati dell'Esempio 2.
Soluzione
L'equazione parametrica del percorso è:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^Due
E l'equazione cartesiana si ottiene risolvendo t dalla prima e sostituendo la seconda
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^Due
Semplificando:
y = 1,73 x - 0,20 x ^ 2
Riferimenti
- P. P. Teodorescu (2007). "Cinematica". Sistemi meccanici, modelli classici: meccanica delle particelle. Springer.
- Resnick, Halliday & Krane (2002). Fisica Volume 1. Cecsa, Messico.
- Thomas Wallace Wright (1896). Elementi di meccanica tra cui cinematica, cinetica e statica. E e FN Spon.
- Wikipedia. Movimento parabolico. Estratto da es.wikipedia.org.
- Wikipedia. Movimento del proiettile Estratto da en.wikipedia.org.

Nessun utente ha ancora commentato questo articolo.