Caratteristiche del tiro parabolico, formule ed equazioni, esempi

Il colpo parabolico Consiste nel lanciare un oggetto o un proiettile con una certa angolazione e lasciarlo muovere sotto l'azione della gravità. Se la resistenza dell'aria non viene considerata, l'oggetto, indipendentemente dalla sua natura, seguirà un percorso ad arco di parabola.

È un movimento quotidiano, poiché tra gli sport più diffusi ci sono quelli in cui si lanciano palloni o palloni, sia con la mano, con il piede o con uno strumento come una racchetta o una mazza per esempio.

Per il suo studio, il tiro parabolico è suddiviso in due movimenti sovrapposti: uno orizzontale senza accelerazione e l'altro verticale con accelerazione costante verso il basso, che è la gravità. Entrambi i movimenti hanno velocità iniziale.

Diciamo che il movimento orizzontale corre lungo l'asse xe il movimento verticale lungo l'asse y. Ciascuno di questi movimenti è indipendente dall'altro.

Poiché la determinazione della posizione del proiettile è l'obiettivo principale, è necessario scegliere un sistema di riferimento appropriato. I dettagli sono di seguito.

Indice articolo

• 1 Formule ed equazioni dei colpi parabolici
  • 1.1 - Traiettoria, altezza massima, tempo massimo e portata orizzontale
• 2 Esempi di tiro parabolico
  • 2.1 Tiro parabolico nelle attività umane
  • 2.2 Il tiro parabolico in natura
• 3 Esercizio
• 4 Riferimenti

Formule ed equazioni dei colpi parabolici

Supponiamo che l'oggetto venga lanciato con angolo α rispetto alla velocità orizzontale e iniziale v_o come mostrato nella figura in basso a sinistra. Il tiro parabolico è un movimento che avviene sull'aereo xy e in quel caso la velocità iniziale si rompe in questo modo:

v_bue = v_o cos α

v_Hey = v_o sin α

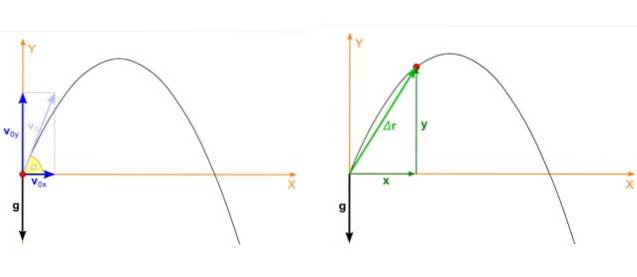
La posizione del proiettile, che è il punto rosso nella figura 2, immagine a destra, ha anche due componenti dipendenti dal tempo, una in X e l'altro in Y. La posizione è un vettore indicato come r e le sue unità sono la lunghezza.

Nella figura, la posizione iniziale del proiettile coincide con l'origine del sistema di coordinate, quindi x_o = 0 e_o = 0. Non è sempre così, puoi scegliere l'origine ovunque, ma questa scelta semplifica notevolmente i calcoli.

Per quanto riguarda i due movimenti in x e in y, questi sono:

-x (t): è un moto rettilineo uniforme.

-y (t): corrisponde a un moto rettilineo uniformemente accelerato con g = 9,8 m / s^Due e puntando verticalmente verso il basso.

In forma matematica:

x (t) = v_o cos α.t

y (t) = v_o .sin α.t - ½g.t^Due

Il vettore di posizione è:

r (t) = [v_o cos α.t]io + [v_o .sin α.t - ½g.t^Due] j

In queste equazioni il lettore attento noterà che il segno meno è dovuto alla gravità puntata verso il suolo, direzione scelta come negativa, mentre verso l'alto è considerata positiva..

Poiché la velocità è la prima derivata della posizione, derivare semplicemente r (t) rispetto al tempo e ottenere:

v (t) = v_o cos α io + (v_o .sin α - gt) j

Infine, l'accelerazione è espressa vettorialmente come:

per (t) = -g j

- Traiettoria, altezza massima, tempo massimo e portata orizzontale

Traiettoria

Per trovare l'equazione esplicita del cammino, che è la curva y (x), dobbiamo eliminare il parametro tempo, risolvendo nell'equazione x (t) e sostituendo in y (t). La semplificazione è alquanto laboriosa, ma alla fine ottieni:

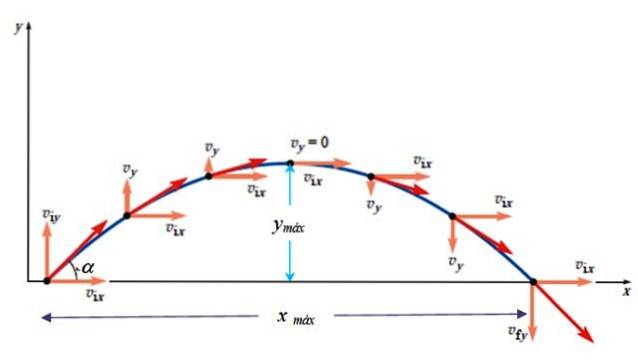
Altezza massima

L'altezza massima si verifica quando v_Y = 0. Sapendo che esiste la seguente relazione tra la posizione e il quadrato della velocità:

v_Y^Due = v_Hey ^Due- 2gy

Fare v_Y = 0 proprio quando si raggiunge l'altezza massima:

0 = v_Hey ^Due- 2g. E_max → e_max = v_Hey ^Due/ 2 g

Con:

v_Hey = v_o senα

Tempo massimo

Il tempo massimo è il tempo impiegato dall'oggetto per raggiungere e_max. Per calcolarlo si usa:

v_Y = v_o .sin α - gt

Sapendo ciò v_Y diventa 0 quando t = t_max, risultato:

v_o .sin α - g.t_max = 0

t_max = v_Hey / g

Massima portata orizzontale e tempo di volo

La portata è molto importante, perché segnala dove cadrà l'oggetto. In questo modo sapremo se colpisce o meno il bersaglio. Per trovarlo abbiamo bisogno del tempo di volo, del tempo totale o di t_v.

Dall'illustrazione sopra è facile concludere che t_v = 2.t_max. Ma attenzione, questo è vero solo se il lancio è a livello, cioè l'altezza del punto di partenza è uguale all'altezza dell'arrivo. Altrimenti il ​​tempo si trova risolvendo l'equazione quadratica risultante dalla sostituzione della posizione finale Y_finale:

Y_finale = v_o .sin α.t_v - ½g.t_v^Due

In ogni caso, la massima portata orizzontale è:

X_max = v_bue. t_v

Esempi di tiro parabolico

Il tiro parabolico fa parte del movimento di persone e animali. Anche di quasi tutti gli sport e giochi in cui interviene la gravità. Per esempio:

Tiro parabolico nelle attività umane

-La pietra lanciata da una catapulta.

-Il calcio di rinvio del portiere.

-La palla lanciata dal lanciatore.

-La freccia che esce dall'arco.

-Tutti i tipi di salti

-Lancia una pietra con una fionda.

-Qualsiasi arma da lancio.

Il tiro parabolico in natura

-Acqua che sgorga da getti naturali o artificiali come quelli di una fontana.

-Pietre e lava che sgorgano da un vulcano.

-Una palla che rimbalza sul pavimento o una pietra che rimbalza sull'acqua.

-Tutti i tipi di animali che saltano: canguri, delfini, gazzelle, gatti, rane, conigli o insetti, solo per citarne alcuni.

Esercizio

Una cavalletta salta con un angolo di 55º rispetto all'orizzontale e atterra a 0,80 metri più avanti. Trova:

a) L'altezza massima raggiunta.

b) Se saltava con la stessa velocità iniziale, ma formando un angolo di 45º, sarebbe andato più in alto??

c) Cosa si può dire della massima estensione orizzontale per questo angolo?

Soluzione a

Quando i dati forniti dal problema non contengono la velocità iniziale v_o i calcoli sono un po 'più laboriosi, ma dalle equazioni note si può derivare una nuova espressione. Partendo da:

X_max = v_bue . t_volo = v_o.cos α. t_v

Quando atterra più tardi, l'altezza torna a 0, quindi:

v_o .sin α.t_v - ½g.t_v^Due= 0

Che cosa t_v è un fattore comune, è semplificato:

v_o .sin α - ½g.t_v= 0

Possiamo cancellare t_v dalla prima equazione:

t_v = x_max / v_o.cos α

E sostituisci nel secondo:

v_o .sin α - (½g. X_max / v_o.cos α) = 0

Moltiplicando tutti i termini per v_o.cos αl'espressione non viene alterata e il denominatore scompare:

(v_o .sin α.) (v_o.cos α) - ½g x_max = 0

v_o^Due sin α. cos α = ½g.x_max

Può già essere cancellato v_o o anche sostituire la seguente identità:

sin 2α = 2 sin α. cos α → v_o^Due peccato 2α = g.x_max

Viene calcolato v_o^Due:

v_o^Due = g.X_max / peccato 2α = (9,8 x 0,8 / seno 110) m^Due/ S^Due = 8,34 m^Due/ S^Due

E infine l'altezza massima:

Y_max= v_Hey ^Due/ 2g = (8,34 x sin^Due 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Soluzione b

L'astice riesce a mantenere la stessa velocità orizzontale, ma diminuendo l'angolo:

Y_max= v_Hey ^Due/ 2g = (8,34 x sin^Due 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Raggiunge un'altezza inferiore.

Soluzione c

La portata orizzontale massima è:

X_max = v_o^Due secondo sen / g

Variando l'angolo, cambia anche la portata orizzontale:

X_max = 8,34 sen 90 / 9.8  m = 0,851 m = 85,1 cm

Adesso il salto è più lungo. Il lettore può verificare che sia massimo per l'angolo di 45º perché:

sin 2α = sin 90 = 1.

Riferimenti

1. Figueroa, D. 2005. Serie: Fisica per le scienze e l'ingegneria. Volume 1. Cinematica. A cura di Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fisica. Seconda edizione. Mcgraw hill.
3. Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
4. Resnick, R. 1999. Fisica. Vol. 1. 3a Ed. In spagnolo. Azienda editoriale Continental S.A. di C.V.
5. Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1.