Il tiro orizzontale È il lancio di un proiettile con velocità orizzontale da una certa altezza e lasciato all'azione della gravità. Senza tener conto della resistenza dell'aria, il percorso descritto dal mobile avrà la forma di un arco di parabola.
La proiezione di oggetti orizzontalmente è abbastanza comune. I proiettili vengono lanciati per tutti i tipi di scopi: dalle pietre con cui sono state colpite le dighe all'inizio della storia, a quelle praticate negli sport con la palla e sono seguite da vicino dalla folla.
Indice articolo
Le caratteristiche principali del tiro orizzontale sono:
-La velocità iniziale data al proiettile è perpendicolare alla gravità.
-Il movimento avviene in un piano, quindi richiede due coordinate: X Y Y.
-Viene eseguito da una certa altezza H sopra il livello del suolo.
-Viene chiamato il tempo in cui il proiettile dura nell'aria tempo di volo.
-Fattori come la resistenza dell'aria e le fluttuazioni del valore di g.
-La forma, le dimensioni e la massa del proiettile non ne influenzano il movimento.
-Il movimento è scomposto in due movimenti simultanei: uno verticale verso il basso sotto l'azione di g; l'altro, orizzontale, a velocità costante.
Le equazioni cinematiche per il lancio orizzontale sono ottenute dalle equazioni per la caduta libera e quelle per il moto rettilineo uniforme..
Come mostra chiaramente l'animazione nella Figura 1, al proiettile viene assegnata una velocità iniziale orizzontale, indicata come vo = vbue io (il grassetto nel testo stampato indica che si tratta di un vettore).
Notare che la velocità iniziale ha ampiezza vbue ed è diretto lungo l'asse X, qual è la direzione del vettore unitario io. L'animazione mostra anche che la velocità iniziale non ha una componente verticale, ma man mano che cade, questa componente aumenta in modo uniforme, grazie all'azione di g, accelerazione di gravità.
Per quanto riguarda la componente orizzontale della velocità, essa rimane costante per tutta la durata del movimento.
Secondo quanto sopra, le posizioni vengono stabilite in funzione del tempo, sia sull'asse orizzontale che sull'asse verticale. La direzione a destra è considerata come l'asse + x, mentre la direzione verso il basso è la direzione -y. Il valore della gravità è g = -9,8 m / sDue o -32 piedi / sDue:
x (t) = xo + vbue.t (posizione orizzontale); vbue è costante
y (t) = yo + vHey.t - ½ g.tDue (posizione verticale); vY = vHey - g.t (velocità verticale)
Le equazioni vengono semplificate scegliendo le seguenti posizioni di partenza: Xo = 0, Yo = 0 nel sito di lancio. Cosa c'è di più vHey = 0, poiché il cellulare è proiettato orizzontalmente. Con questa scelta le equazioni del moto sono così:
x (t) = vbue.t; vX = vbue
y (t) = - ½ g.tDue; vY = - g.t
Quando il tempo non è disponibile, è utile l'equazione che mette in relazione velocità e spostamenti. Questo vale per la velocità verticale, poiché l'orizzontale rimane costante durante tutto il movimento:
vYDue = vHeyDue + 2.g .y = 2.g.y
Per calcolare il tempo di volo tvolo, supponiamo che il mobile sia proiettato da un'altezza H sul pavimento. Poiché l'origine del sistema di riferimento è stata scelta nel punto di lancio, quando raggiunge il suolo è nella posizione -H. Sostituendolo nell'equazione 2) otteniamo:
-H = - ½ g.tDuevolo
tvolo = (2H / g)½
Il portata orizzontale si ottiene sostituendo questa volta in x (t):
Xmax = vbue. (2H / g)½
Un elicottero vola orizzontalmente, mantenendo un'altitudine costante di 580 m quando fa cadere una scatola contenente cibo su un campo profughi. La scatola atterra a una distanza orizzontale di 150 m dal punto di lancio. Trova: a) Il tempo di volo della scatola.
b) La velocità dell'elicottero.
c) Quanto velocemente la scatola ha toccato il suolo??
a) L'altezza H da cui viene fatto cadere il cibo è H = 500 m. Con questi dati, in caso di sostituzione, si ottiene:
tvolo = (2H / g)½= (2 x 580 / 9,8) ½s = 10,9 s
b) L'elicottero trasporta la velocità orizzontale iniziale vbue del pacchetto e poiché uno dei dati è Xmax:
Xmax = vbue. (2H / g)½ ® vbue = xmax / (2H / g)½= xmax / tvolo = 150 m / 10,9 s = 13,8 m / s
c) La velocità del proiettile in ogni istante è:
vY = -g.t = -9,8 m / sDue x 10,9 s = -106,82 m / s = - 384,6 km / h
Il segno negativo indica che il cellulare si sta muovendo verso il basso.
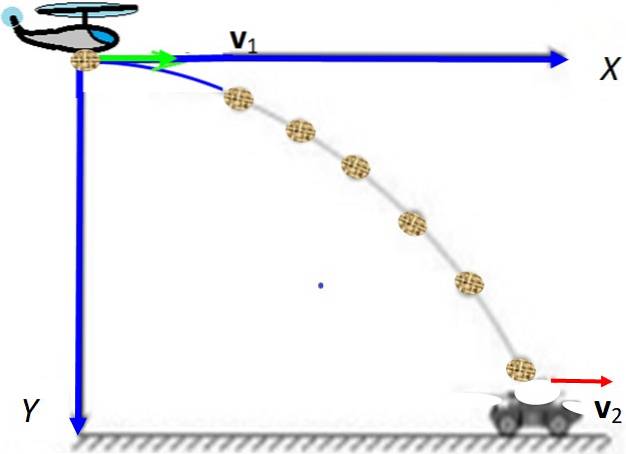
Da un aeroplano che vola orizzontalmente ad un'altezza H = 500 m Y 200 km / h un pacco cade e deve cadere su un veicolo aperto che si sta muovendo 18 km / h sulla strada. In quale posizione l'aereo deve far cadere il pacco in modo che cada nel veicolo? Non tenere in considerazione la resistenza dell'aria o la velocità del vento.
È conveniente passare prima tutte le unità al Sistema Internazionale:
18 km / h = 6 m / s
200 km / h = 55 m / s
Ci sono due cellulari: aereo (1) e veicolo (2) ed è necessario scegliere un sistema di coordinate per localizzarli entrambi. È conveniente farlo al punto di partenza del pacchetto sull'aereo. Il pacco viene proiettato orizzontalmente con la velocità che sta trasportando l'aereo: v1, mentre il veicolo si sta muovendo a vDue assunta costante.
-Aereo
Posizione iniziale: x = 0; y = 0
Velocità iniziale = v1 (orizzontale)
Equazioni di posizione: y (t) = -½g.tDue ; x (t) = v1.t
-Veicolo
Posizione iniziale: x = 0, y = -H
Velocità iniziale = vDue (costante)
x (t) = xo + vDue. t
La durata del volo del pacchetto è:
tvolo = (2H / g)½ = (2 × 500 / 9,8)½s = 10,1 s
In questo lasso di tempo, il pacco ha subito uno spostamento orizzontale di:
Xmax = vbue . (2H / g)½= 55 m / s x 10,1 s = 556 m.
In questo lasso di tempo, il veicolo si è mosso anche in orizzontale:
x (t) = v1.t = 6 m / s x10,1 s = 60,6 m
Se l'aereo lascia cadere il pacco immediatamente quando vede il veicolo che vi passa sotto, non lo farà cadere direttamente al suo interno. Affinché ciò accada, devi buttarlo più indietro:
d = 556 m - 60,6 m = 495,4 m.
Nessun utente ha ancora commentato questo articolo.