Teorema di Varignon

Qual è il teorema di Varignon?

Il teorema di Varignon, in Meccanica, afferma che la somma dei momenti prodotti da un sistema di forze concorrenti rispetto ad un certo punto è uguale al momento della forza risultante rispetto allo stesso punto.

Per questo motivo questo teorema è noto anche come l'inizio dei momenti.

Sebbene il primo ad enunciarlo sia stato l'olandese Simon Stevin (1548-1620), l'ideatore del paradosso idrostatico, il matematico francese Pierre Varignon (1654-1722) fu colui che in seguito gli diede la sua forma definitiva.

Un esempio di come funziona il teorema di Varignon in Meccanica è il seguente: supponiamo che un semplice sistema di due forze complanari e concorrenti agisca su un punto F₁ Y F_Due, (indicato in grassetto a causa del loro carattere vettoriale). Queste forze danno origine a una forza netta o risultante, chiamata F_R.

Ogni forza esercita una coppia o un momento attorno a un punto O, che viene calcolato dal prodotto vettoriale tra il vettore di posizione r_OPERAZIONE e la forza F, dove r_OPERAZIONE è diretto da O al punto di concorrenza P:

M_O1 = r_OPERAZIONE × F₁

M_O2 = r_OPERAZIONE × F_Due

dato che F_R = F₁ + F_Due, poi:

M_O = r_OPERAZIONE × F₁ + r_OPERAZIONE × F_Due = M_O1 + M_O2

Ma come r_OPERAZIONE è un fattore comune, quindi, l'applicazione della proprietà distributiva al prodotto incrociato:

M_O = r_OPERAZIONE × (F₁ + F_Due) = r_OPERAZIONE × F_R                

Pertanto, la somma dei momenti o delle coppie di ciascuna forza rispetto al punto O è equivalente al momento della forza risultante rispetto allo stesso punto.

Dichiarazione e prova

Sia un sistema di N forze concorrenti, formato da F₁, F_Due, F₃... F_N, le cui linee di azione si intersecano nel punto P (vedi figura 1), momento di questo sistema di forze M_O, rispetto ad un punto O è dato da:

M_O = r_OPERAZIONE × F₁ + r_OPERAZIONE × F_Due + r_OPERAZIONE × F₃ +... r_OPERAZIONE × F_N = r_OPERAZIONE × (F₁ + F_Due + F₃ +... F_N)

Dimostrazione

Per dimostrare il teorema, si usa la proprietà distributiva del prodotto vettoriale tra vettori.

Sii le forze F₁, F_Due, F₃... F_N applicato ai punti A₁, PER_Due, PER₃… PER_N e concorrente al punto P. Il momento risultante di questo sistema, rispetto ad un punto O, chiamato M_O, è la somma dei momenti di ciascuna forza, rispetto a detto punto:

M_O = ∑ r_OAi × F_io

Dove la somma va da i = 1 a i = N, poiché ci sono N forze. Trattandosi di forze concorrenti e poiché il prodotto vettoriale tra vettori paralleli è zero, accade che:

r_PAi × F_io = 0

Con il vettore nullo indicato come 0.

Il momento di una delle forze rispetto a O, ad esempio quello della forza F_io applicato in A_io, è scritto così:

M_{ho sentito} = r_OAi × F_io

Il vettore di posizione r_OAi  può essere espresso come la somma di due vettori di posizione:

r_OAi = r_OPERAZIONE + r_PAi

In questo modo, il momento circa O della forza F_io è:

M_{ho sentito} = (r_OPERAZIONE + r_PAi) × F_io = (r_OPERAZIONE × F_io) + (r_PAi × F_io)

Ma l'ultimo termine è nullo, come spiegato sopra, perché r_PAi è sulla linea di azione di F_io, Quindi:

M_{ho sentito} = r_OPERAZIONE × F_io

Sapendo che il momento del sistema rispetto al punto O è la somma di tutti i singoli momenti di ciascuna forza rispetto a detto punto, allora:

M_O = ∑ M_{ho sentito} = ∑ r_OPERAZIONE × F_io

Che cosa r_OPERAZIONE è costante esce dalla somma:

M_O = r_OPERAZIONE × (∑ F_io)

Ma ∑ F_io è semplicemente la forza netta o la forza risultante F_R, si conclude quindi immediatamente che:

M_O = r_OPERAZIONE × F_R

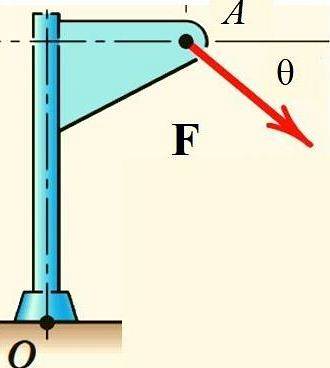
Esempio

Il teorema di Varignon facilita il calcolo del momento di forza F Rispetto al punto O nella struttura mostrata in figura, se la forza viene scomposta nelle sue componenti rettangolari e si calcola il momento di ciascuna di esse:

Applicazioni del teorema di Varignon

Quando la forza risultante di un sistema è nota, il teorema di Varignon può essere applicato per sostituire la somma di ciascuno dei momenti prodotti dalle forze che lo compongono dal momento della risultante.

Se il sistema è costituito da forze sullo stesso piano e il punto rispetto al quale si vuole calcolare il momento appartiene a quel piano, il momento risultante è perpendicolare.

Ad esempio, se tutte le forze sono nel piano xy, il momento è diretto sull'asse z e non resta che trovare la sua grandezza e il suo senso, come nel caso dell'esempio sopra descritto.

In questo caso, il teorema di Varignon ci permette di calcolare il momento risultante del sistema tramite la somma. È molto utile nel caso di un sistema di forza tridimensionale, per il quale la direzione del momento risultante non è nota a priori.

Per risolvere questi esercizi, è conveniente scomporre le forze e posizionare i vettori nelle loro componenti rettangolari e, dalla somma dei momenti, determinare le componenti del momento netto.

Esercizio risolto

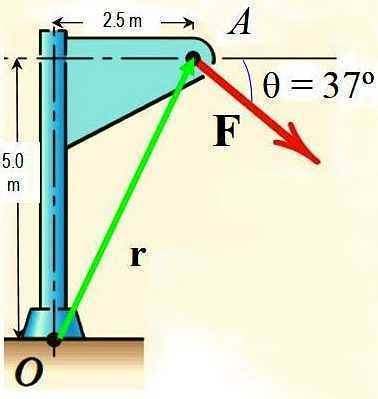
Usando il teorema di Varignon, calcola il momento della forza F attorno al punto O mostrato in figura se la grandezza di F è 725 N.

Soluzione

Per applicare il teorema di Varignon, scomponi la forza F in due componenti, i cui rispettivi momenti intorno a O vengono calcolati e sommati per ottenere il momento risultante.

F_X = 725 N ∙ cos 37 º = 579,0 N

F_Y = - 725 N N ∙ sin 37 º = −436,3 N

Allo stesso modo, il vettore di posizione r diretto da O ad A ha i componenti:

r_X = 2,5 m

r_Y = 5,0 m

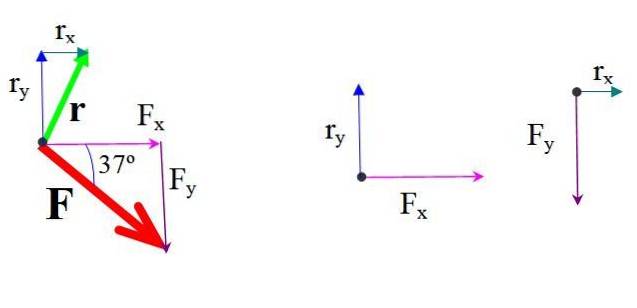
Il momento di ciascuna componente della forza attorno a O si trova moltiplicando la forza e la distanza perpendicolare.

Entrambe le forze tendono a ruotare la struttura nella stessa direzione, che in questo caso è in senso orario, a cui viene arbitrariamente assegnato un segno positivo:

M_Bue = F_X∙ r_Y ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m

M_Oy = F_Y∙ r_X ∙ sin (−90º) = −436,3 N ∙ 2,5 m ∙ (−1) = 1090,8 N ∙ m

Il momento risultante su O è:

M_O = M_Bue + M_Oy = 3985,8 N ∙ m perpendicolare al piano e in senso orario.

Riferimenti

1. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
2. Beer, F. 2010. Statico. McGraw Hill. 9 °. Edizione.
3. Hibbeler, R. 1992. Meccanica per ingegneri. 6 °. Edizione. CECSA.
4. HK Engineering. Teorema di Varignon. Estratto da: youtube.com.
5. Wikipedia. Teorema di Varignon (Meccanica). Estratto da: en.wikipedia.org.